Коэффициент вязкости — это… Что такое Коэффициент вязкости?
Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.
Прибор для измерения вязкости называется вискозиметром.
Вязкость газов
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
,
где — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.
Вторая вязкость
Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.
Вязкость жидкостей
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = Cew / kT
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.
Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.
Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
Вязкость аморфных материалов
Вязкость аморфных материалов (например, стекла или расплавов), это термически активизируемый процесс[1]:
где Q — энергия активации вязкости (кДж/моль), T — температура (К), R
Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины QH при низких температурах (в стеклообразном состоянии) на малую величину QL при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:
с постоянными A1, A
2, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.В узких температурных интервалах недалеко от температуры стеклования Tg это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.
Вязкость
Если температура существенно ниже температуры стеклования T < Tg, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса
с высокой энергией активации QH = Hd + Hm, где Hd — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а Hm — энтальпия их движения. Это связано с тем, что при T < Tg
Это связано с тем, что при T < Tg
При T > > Tg двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса
но с низкой энергией активации QL = Hm. Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.
Сила вязкого трения
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя.
Примечания
- ↑ Я. И. Френкель. Кинетическая теория жидкостей. Ленинград, Наука, 1975.
См. также
Ссылки
- Аринштейн А., Сравнительный вискозиметр Жуковского Квант, № 9, 1983.
- Измерение вязкости нефтепродуктов — обзор методов и единиц измерения вязкости.
- R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
- M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
- M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
- Булкин П. С. Попова И. И.,Общий физический практикум. Молекулярная физика
- Статья в энциклопедии Химик.ру
Литература
- Я. И. Френкель. Кинетическая теория жидкостей. — Л.: «Наука», 1975.
Коэффициент вязкости — это… Что такое Коэффициент вязкости?
Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.
Прибор для измерения вязкости называется вискозиметром.
Вязкость газов
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
,
где — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.
Вторая вязкость
Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.
Вязкость жидкостей
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = Ce
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.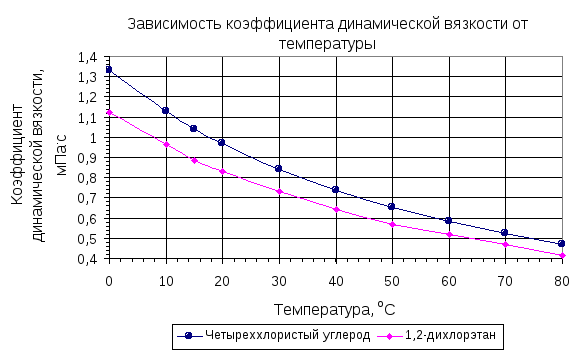
Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
Вязкость аморфных материалов
Вязкость аморфных материалов (например, стекла или расплавов), это термически активизируемый процесс [1]:
где Q — энергия активации вязкости (кДж/моль), T — температура (К), R — универсальная газовая постоянная (8,31 Дж/моль•К) и A — некоторая постоянная.
Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины QH при низких температурах (в стеклообразном состоянии) на малую величину QL при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:
с постоянными A1, A2, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.
В узких температурных интервалах недалеко от температуры стеклования Tg это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.
Вязкость
Если температура существенно ниже температуры стеклования T < Tg, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса
с высокой энергией активации QH = Hd + Hm, где Hd — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а Hm — энтальпия их движения. Это связано с тем, что при T < Tg аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.
Это связано с тем, что при T < Tg аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.
При T > > Tg двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса
но с низкой энергией активации QL = Hm. Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.
Сила вязкого трения
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.
Это отличает вязкое трение от сухого.
Примечания
- ↑ Я. И. Френкель. Кинетическая теория жидкостей. Ленинград, Наука, 1975.
См. также
Ссылки
- Аринштейн А., Сравнительный вискозиметр Жуковского Квант, № 9, 1983.
- Измерение вязкости нефтепродуктов — обзор методов и единиц измерения вязкости.
- R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
- M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
- M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
- Булкин П. С. Попова И. И.,Общий физический практикум. Молекулярная физика
- Статья в энциклопедии Химик.ру
Литература
- Я. И. Френкель. Кинетическая теория жидкостей. — Л.: «Наука», 1975.
Wikimedia Foundation. 2010.
Коэффициент вязкости — это… Что такое Коэффициент вязкости?
Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.
Прибор для измерения вязкости называется вискозиметром.
Вязкость газов
В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
,
где — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.
Вторая вязкость
Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.
Вязкость жидкостей
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = Cew / kT
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества VM. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.
Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
Вязкость аморфных материалов
Вязкость аморфных материалов (например, стекла или расплавов), это термически активизируемый процесс[1]:
где Q — энергия активации вязкости (кДж/моль), T — температура (К), R — универсальная газовая постоянная (8,31 Дж/моль•К) и A — некоторая постоянная.
Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины QH при низких температурах (в стеклообразном состоянии) на малую величину QL при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют RD < 2, в то время как ломкие материалы имеют .
Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:
с постоянными A1, A2, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.
В узких температурных интервалах недалеко от температуры стеклования Tg это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.
Вязкость
Если температура существенно ниже температуры стеклования T < Tg, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса
с высокой энергией активации QH = Hd + Hm, где Hd — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а Hm — энтальпия их движения. Это связано с тем, что при T < Tg аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.
Это связано с тем, что при T < Tg аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.
При T > > Tg двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса
но с низкой энергией активации QL = Hm. Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.
Сила вязкого трения
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.
Это отличает вязкое трение от сухого.
Примечания
- ↑ Я. И. Френкель. Кинетическая теория жидкостей. Ленинград, Наука, 1975.
См. также
Ссылки
- Аринштейн А., Сравнительный вискозиметр Жуковского Квант, № 9, 1983.
- Измерение вязкости нефтепродуктов — обзор методов и единиц измерения вязкости.
- R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
- M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
- M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
- Булкин П. С. Попова И. И.,Общий физический практикум. Молекулярная физика
- Статья в энциклопедии Химик.ру
Литература
- Я. И. Френкель. Кинетическая теория жидкостей. — Л.: «Наука», 1975.
Wikimedia Foundation. 2010.
Коэффициент вязкости, формула и примеры
Определение и формула коэффициента вязкости
Выделяют динамическую вязкость и кинематическую.
Рассмотрим движение газа, обладающего вязкостью как перемещение плоских параллельных слоев. Будем считать, что изменение скорости движения вещества происходит по направлению оси X, которая перпендикулярна к направлению скорости движения газа (рис.1).
Рис. 1
В направлении оси Y скорость движения во всех точках одинакова. Значит, скорость является функцией . В таком случае, модуль силы трения между слоями газа (F), которая действует на единицу площади поверхности, которая разделяет два соседних слоя, описывается уравнением:
где — градиент скорости () по оси X. Ось X перепендикулярна направлению движения слоев вещества (рис.1).
Определение
Коэффициент (), входящий в уравнение (1) называется коэффициентом динамической вязкости (коэффициентом внутреннего трения). Он зависит от свойств газа (жидкости). численно равен количеству движения, которое переносится в единицу времени через площадку единичной площади при градиенте скорости равном единице, в направлении перпендикулярном площадке. Или численно равен силе, которая действует на единицу площади при градиенте скорости, равном единице.
Или численно равен силе, которая действует на единицу площади при градиенте скорости, равном единице.
Внутренне трение — причина того, что для течения газа (жидкости) сквозь трубу необходима разность давлений. При этом, чем больше коэффициент вязкости вещества, тем больше должна быть разность давлений для придания заданной скорости течению.
Коэффициент кинематической вязкости обычно, обозначают . Он равен:
где — плотность газа (жидкости).
Коэффициент внутреннего трения газа
В соответствии с кинетической теорией газов коэффициент вязкости можно вычислить при помощи формулы:
где — средняя скорость теплового движения молекул газа, — средняя длина свободного пробега молекулы. Выражение (3) показывает, что при низом давлении (разреженный газ) вязкость почти не зависит от давления, так как Но такой вывод справедлив до момента, пока отношение длины свободного пробега молекулы к линейным размерам сосуда не станет приблизительно равным единице. При увеличении температуры вязкость газов обычно растет, так как
При увеличении температуры вязкость газов обычно растет, так как
Коэффициент вязкости жидкостей
Считая, что коэффициент вязкости определен силами взаимодействия молекул вещества, которые зависят от среднего расстояния между ними, то коэффициент вязкости определяют экспериментальной формулой Бачинского:
где — молярный объем жидкости, А и B — постоянные величины.
Вязкость жидкостей с ростом температуры уменьшается, при увеличении давления растет.
Формула Пуазейля
Коэффициент вязкости входит в формулу, которая устанавливает зависимость между объемом (V) газа, который протекает в единицу времени через сечение трубы и необходимой для этого разностью давлений ():
где — длина трубы, — радиус трубы.
Число Рейнольдса
Характер движения газа (жидкости) определяется безразмерным числом Рейнольдса ():
— величина, которая характеризует линейные размеры тела, обтекаемого жидкостью (газом).
Единицы измерения коэффициента вязкости
Основной единицей измерения коэффициента динамической вязкости в системе СИ является:
=Па• c
В СГС:
=пуаз
1Па• c=10 пуаз
Основной единицей измерения коэффициента кинематической вязкости в системе СИ является:
В СГС:
=стокc
Примеры решения задач
Метод определения кинематической вязкости и расчет динамической вязкости прозрачных и непрозрачных жидкостей – РТС-тендер
ГОСТ 33768-2015
МКС 75.080
Дата введения 2017-02-01
Цели, основные принципы и общие правила проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
Правила разработки, принятия, обновления и отмены»
Сведения о стандарте
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт расходометрии» (ФГУП «ВНИИР»)
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 10 декабря 2015 г. N 48)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Казахстан | KZ | Госстандарт Республики Казахстан |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
Узбекистан | UZ | Узстандарт |
(Поправка, ИУС N 2-2019)
4 Приказом Федерального агентства по техническому регулированию и метрологии от 17 ноября 2016 г. N 1704-ст межгосударственный стандарт ГОСТ 33768-2015 введен в действиев качестве национального стандарта Российской Федерации с 1 февраля 2017 г.
N 1704-ст межгосударственный стандарт ГОСТ 33768-2015 введен в действиев качестве национального стандарта Российской Федерации с 1 февраля 2017 г.
5 ВВЕДЕН ВПЕРВЫЕ
6 ИЗДАНИЕ (август 2019 г.) с Поправкой (ИУС 2-2019)
Информация о введении в действие (прекращении действия) настоящего стандарта и изменений к нему на территории указанных выше государств публикуется в указателях национальных стандартов, издаваемых в этих государствах, а также в сети Интернет на сайтах соответствующих национальных органов по стандартизации.
В случае пересмотра, изменения или отмены настоящего стандарта соответствующая информация будет опубликована на официальном интернет-сайте Межгосударственного совета по стандартизации, метрологии и сертификации в каталоге «Межгосударственные стандарты»
Настоящий стандарт распространяется на прозрачные и непрозрачные нефтепродукты, жидкие при температуре испытания, у которых напряжение сдвига пропорционально скорости деформации (ньютоновские жидкости).
Стандарт устанавливает метод определения кинематической вязкости нефтепродуктов стеклянным капиллярным вискозиметром, а также расчет динамической вязкости.
Настоящий стандарт не распространяется на битумы.
Примечание — В стандарт также включена процедура испытания и показатели точности для остаточных котельных топлив (мазутов), которые в определенных условиях проявляют свойства неньютоновских жидкостей.
В настоящем стандарте использованы ссылки на следующие межгосударственные стандарты:
ГОСТ 400-80 Термометры стеклянные для испытания нефтепродуктов. Технические условия
ГОСТ 2517-2012 Нефть и нефтепродукты. Методы отбора проб
ГОСТ 2603-79 Реактивы. Ацетон. Технические условия
ГОСТ 3118-77 Реактивы. Кислота соляная. Технические условия
ГОСТ 4095-75 Изооктан технический. Технические условия
ГОСТ 4204-77 Реактивы.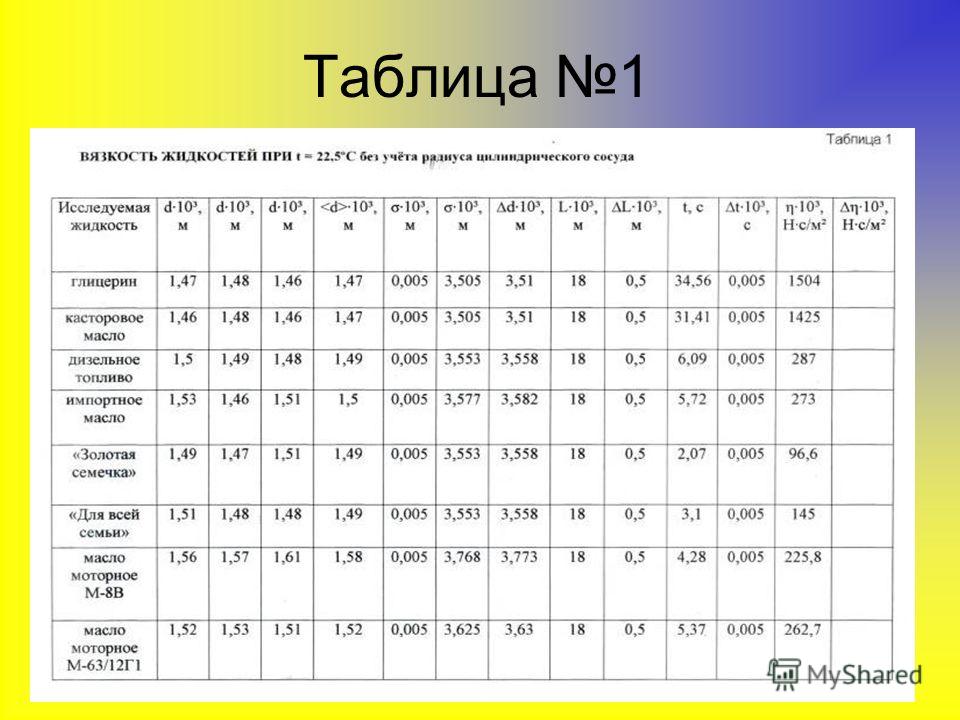 Кислота серная. Технические условия
Кислота серная. Технические условия
ГОСТ 4220-75 Реактивы. Калий двухромовокислый. Технические условия
ГОСТ 5789-78 Реактивы. Толуол. Технические условия
ГОСТ 6709-72 Вода дистиллированная. Технические условия
ГОСТ 6824-96 Глицерин дистиллированный. Общие технические условия
ГОСТ 8505-80 Нефрас-С 50/170. Технические условия
ГОСТ 12026-76 Бумага фильтровальная лабораторная. Технические условия
ГОСТ 10028-81 Вискозиметры капиллярные стеклянные. Технические условия
ГОСТ 13646-68 Термометры стеклянные ртутные для точных измерений. Технические условия
ГОСТ 14710-78 Толуол нефтяной. Технические условия
ГОСТ 17299-78 Спирт этиловый технический. Технические условия
ГОСТ 18300-87 Спирт этиловый ректификованный технический. Технические условия
________________
В Российской Федерации действует ГОСТ Р 55878-2013 «Спирт этиловый технический гидролизный ректификованный. Технические условия».
Технические условия».
ГОСТ 22867-77 Реактивы. Аммоний азотнокислый. Технические условия
ГОСТ 25336-82 Посуда и оборудование лабораторные стеклянные. Типы, основные параметры и размеры
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов и классификаторов на официальном интернет-сайте Межгосударственного совета по стандартизации, метрологии и сертификации (www.easc.by) или по указателям национальных стандартов, издаваемым в государствах, указанных в предисловии, или на официальных сайтах соответствующих национальных органов по стандартизации. Если на документ дана недатированная ссылка, то следует использовать документ, действующий на текущий момент, с учетом всех внесенных в него изменений. Если заменен ссылочный документ, на который дана датированная ссылка, то следует использовать указанную версию этого документа. Если после принятия настоящего стандарта в ссылочный документ, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение применяется без учета данного изменения. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1 динамическая вязкость (коэффициент динамической вязкости): Отношение напряжения сдвига, возникающего при движении слоев жидкости относительно друг друга, к скорости деформации (скорость, с которой слои движутся друг относительно друга). Динамическая вязкость является мерой сопротивления течению или деформируемости жидкости.
3.2 кинематическая вязкость: Отношение динамической вязкости жидкости к ее плотности при той же температуре. Кинематическая вязкость является мерой сопротивления течению жидкости под влиянием силы тяжести (силы гравитации).
3.3 ньютоновская жидкость: Жидкость, для которой динамическая вязкость не зависит от напряжения сдвига и скорости деформации. Если отношение напряжения сдвига к скорости деформации не постоянно, жидкость не является ньютоновской.
Если отношение напряжения сдвига к скорости деформации не постоянно, жидкость не является ньютоновской.
Примечание — Для проверки свойств жидкости следует измерить кинематическую вязкость жидкости при одной и той же температуре в двух капиллярных однотипных вискозиметрах, постоянные которых отличаются не менее чем в два раза. При соответствии результатов определения вязкости в пределах величины повторяемости, приведенной в таблице 1, следует считать испытуемую жидкость ньютоновской.
Сущность метода заключается в измерении стеклянным капиллярным вискозиметром времени истечения определенного объема испытуемого нефтепродукта под влиянием силы тяжести. Кинематическая вязкость вычисляется как произведение измеренного времени истечения нефтепродукта и постоянной вискозиметра. Динамическая вязкость вычисляется как произведение кинематической вязкости и плотности нефтепродукта при одной и той же температуре.
5.1 Повторяемость d
Расхождение результатов двух последовательных измерений времени истечения, полученных одним и тем же исполнителем, работающим в одной и той же лаборатории на одном и том же оборудовании, при постоянных условиях и на идентичных образцах одной и той же пробы нефтепродукта, не должно превышать (с доверительной вероятностью 95%) значений, приведенных в таблице 1.
5.2 Повторяемость (сходимость) r
Расхождение результатов двух последовательных значений кинематической вязкости, полученных одним и тем же исполнителем, работающим в одной и той же лаборатории на одном и том же оборудовании, при постоянных условиях и на идентичных образцах одной и той же пробы нефтепродукта, не должно превышать (с доверительной вероятностью 95%) значений повторяемости, приведенных в таблице 1.
5.3 Воспроизводимость R
Расхождение результатов двух единичных и независимых значений кинематической вязкости, полученных разными исполнителями, работающими в разных лабораториях на идентичных образцах одной и той же пробы нефтепродукта, не должно превышать (с доверительной вероятностью 95%) значений, приведенных в таблице 1.
Таблица 1 — Показатели точности метода
Испытуемый продукт | Повторяемость d | Повторяемость r | Воспроиз- |
Базовые масла при 40°C и 100°C | 0,0020y | 0,0011x | 0,0065x |
(0,20%) | (0,11%) | (0,65%) | |
Компаундированные масла при 40°C и 100°C | 0,0013y | 0,0026x | 0,0076x |
(0,13%) | (0,26%) | (0,76%) | |
Компаундированные масла при 150°C | 0,015y | 0,0056x | 0,018x |
(1,5%) | (0,56%) | (1,8%) | |
Нефтяные парафины при 100°C | 0,0080y (0,80%) | 0,0141x | 0,0366x |
Остаточные котельные топлива (мазуты) при 80°C и 100°C | 0,011(y+8) | 0,013(x+8) | 0,04(x+8) |
Остаточные котельные топлива (мазуты) при 50°C | 0,017y | 0,015x | 0,074x |
(1,7%) | (1,5%) | (7,4%) | |
Добавка к смазочному маслу при 100°C | 0,00106·y | 0,00192·y | 0,00862·x |
Среднедистиллятное топливо при 40°C | 0,0013(y+1) | 0,0043(x+1) | 0,0082(x+1) |
Авиационное топливо для газотурбинных двигателей при минус 20°C | 0,0018y | 0,007x | 0,019x |
(0,18%) | (0,7%) | (1,9%) | |
Прочие нефтепродукты | — | 0,0035x | 0,0072x |
(0,35%) | (0,72%) | ||
Обозначения: y — среднеарифметическое значение двух сравниваемых результатов измерений времени истечения, с; x — среднеарифметическое значение двух сравниваемых результатов измерений вязкости, мм/с. | |||
6.1 Вискозиметры стеклянные капиллярные, обеспечивающие измерение кинематической вязкости с точностью, указанной в таблице 1.
Примечания
1 Типы наиболее часто применяемых вискозиметров, со спецификацией удовлетворяющей требованиям, указанным в [1]* и обеспечивающие измерение кинематической вязкости с точностью, указанной в таблице 1, приведены в таблице А.1 (приложение А).
________________
* Поз. [1] см. раздел Библиография, здесь и далее по тексту. — Примечание изготовителя базы данных.
2 Для каждого диапазона вязкости необходимо иметь набор однотипных вискозиметров.
6.2 Держатели, обеспечивающие строго вертикальное крепление вискозиметра.
6.3 Отвес для проверки вертикальности расположения вискозиметра.
6.4 Штативы или другие устройства для крепления термометра в вертикальном направлении.
6.5 Термостат, криостат или баня с регулируемой температурой.
Глубина термостата должна быть такой, чтобы расстояния от нефтепродукта в вискозиметре до уровня термостатирующей жидкости в термостате и от нефтепродукта до дна термостата были не менее 20 мм.
Регулирование температуры термостатирующей жидкости в термостате должна быть такой, чтобы во время проведения измерений времени истечения температура жидкости в термостате не отклонялась от заданного значения и не менялась по всей высоте вискозиметров, а также в пространстве между вискозиметрами и местом расположения термометра, более чем на ±0,02°C при температуре от 15°C до 100°C и ±0,05°C при температуре вне этого диапазона.
Примечания
1 Для охлаждения термостатирующей жидкости допускается использовать лед, твердую углекислоту (сухой лед), жидкий азот.
2 Для определения вязкости при температуре ниже 15°C допускается применять прозрачные сосуды Дьюара соответствующей вместимости.
6.6 Термостатирующие жидкости.
В качестве термостатирующих жидкостей применяют жидкости, остающиеся жидкими и прозрачными при температуре испытания. В зависимости от температуры испытания нефтепродукта для заполнения термостата используют следующие жидкости:
— от минус 60°C до 15°C — спирт этиловый технический по ГОСТ 17299, спирт этиловый ректификованный технический по ГОСТ 18300, или изооктан технический по ГОСТ 4095;
— свыше 15°C до плюс 60°C — вода дистиллированная;
— свыше 60°C до плюс 90°C — глицерин по ГОСТ 6824, разбавленный водой в соотношении 1:1, или светлое нефтяное масло;
— свыше 90°C — 25%-ный раствор азотнокислого аммония по ГОСТ 22867.
6.7 Жидкостные стеклянные термометры типов I и II по ГОСТ 13646, типа ТИН-10 по ГОСТ 400 и типа ASTM, IP и ASTM/IP, соответствующие приложению Б.
Для диапазона измерений от 0°C до 100°C применяют жидкостные стеклянные термометры с точностью после корректировки (введения поправок на показания, указанных в свидетельстве о поверке) не менее ±0,02°C, при применении двух термометров в одном и том же термостате их показания не должны отличаться более чем на ±0,04°C.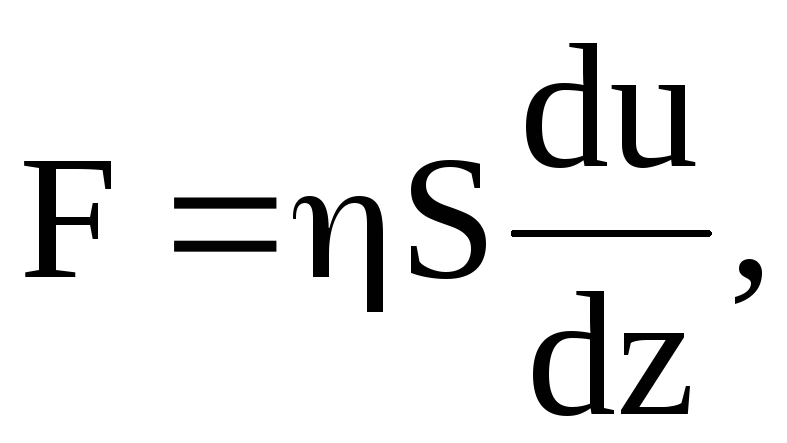
Для измерения температур вне диапазона от 0°C до 100°C следует использовать жидкостные стеклянные термометры с точностью после корректировки не менее ±0,05°C, при применении двух термометров в одном и том же термостате их показания не должны отличаться более чем на ±0,1°C.
Примечание — Допускается применять другие термометрические устройства равноценной или более высокой точности.
6.8 Устройства, обеспечивающие отсчет времени с дискретностью до 0,1 с и имеющие погрешность не более ±0,07%.
Примечания
1 Допускается применять секундомеры, обеспечивающие отсчет времени до 0,2 с. При применении секундомеров, обеспечивающих отсчет времени до 0,2 с, расхождения между последовательными определениями времени истечения продукта в одном и том же вискозиметре не должны превышать значений, указанных в таблице 1.
2 Допускается применять электрические устройства для измерения времени, если частота тока контролируется с точностью не ниже 0,05%.
6.9 Шкаф сушильный, обеспечивающий температуру от 100°C до 200°C.
6.10 Фильтры с размером отверстий 75 мкм, воронки или тигли фильтрующие по ГОСТ 25336.
Примечание — Для фильтрования жидкостей с вязкостью более 2000 мм/с допускается применять фильтры с размером ячейки не превышающим 0,6 мм.
6.11 Бумага фильтровальная лабораторная по ГОСТ 12026.
6.12 Соль поваренная крупнокристаллическая или сульфат натрия безводный, или кальций хлористый прокаленный, или любой другой осушитель.
6.13 Нефрас по ГОСТ 8505.
6.14 Ацетон по ГОСТ 2603.
6.15 Толуол по ГОСТ 5789.
6.16 Спирт этиловый технический по ГОСТ 17299, спирт этиловый ректификованный технический по ГОСТ 18300.
6.17 Эфир петролейный.
6.18 Смесь хромовая для мойки стекла: калий двухромовый кислый по ГОСТ 4220, кислота серная по ГОСТ 4204 или сильно окисляющая кислота, не содержащая хрома.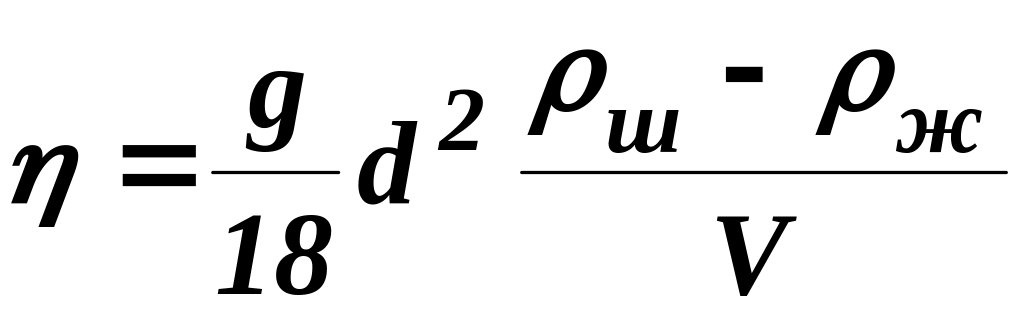
Примечание — Хромовая кислота и растворы сильных кислот опасны для здоровья (токсичны, чрезвычайно коррозионно-агресивны и потенциально опасны при контакте с органическими веществами). При их применении необходимо защитить все лицо и надеть защитную одежду, не вдыхать пары, отходы разложить в соответствии со стандартными методиками.
6.19 Кислота соляная по ГОСТ 3118.
6.20 Вода дистиллированная по ГОСТ 6709.
6.21 Сертифицированные стандартные образцы вязкости, используемые для контроля точности измерений.
Примечание — Допускается применять реактивы и растворители с квалификацией не ниже указанной в настоящем стандарте.
7.1 Устанавливают и поддерживают в термостате необходимую температуру испытания нефтепродукта с учетом требований указанных в 6.5.
Примечание — Температура испытания образца нефтепродукта должна обеспечивать свободное истечение нефтепродукта через капилляр вискозиметра и получение идентичных результатов при использовании вискозиметров с различными диаметрами капилляров.
Температуру жидкости в термостате измеряют жидкостными стеклянными термометрами, погруженными в жидкость. Термометры должны крепиться вертикально при той же глубине погружения, что и при калибровке.
Примечание — Для получения наиболее достоверных результатов измерения температуры жидкости рекомендуется одновременно использовать два термометра с учетом поправок из свидетельства о поверке. За результат измерения температуры жидкости принимается среднеарифметическое значение показаний двух термометров с учетом всех поправок.
При частичном погружении в жидкость термометра, градуированного на полное погружение, в показания термометра вводят поправку на выступающий над поверхностью жидкости столбик термометрической жидкости, вычисляемую по формуле
, (1)
где — поправка на выступающий столбик термометрической жидкости, °С;
— коэффициент, равный для ртутного термометра 0,00016, для спиртового термометра — 0,001;
— высота выступающего столбика термометрической жидкости, выраженная в градусных делениях шкалы термометра;
— показание термометра, °С;
— температура окружающего воздуха вблизи середины выступающего столбика термометрической жидкости (определяется вспомогательным термометром, резервуар которого находится на середине высоты выступающего столбика), °С.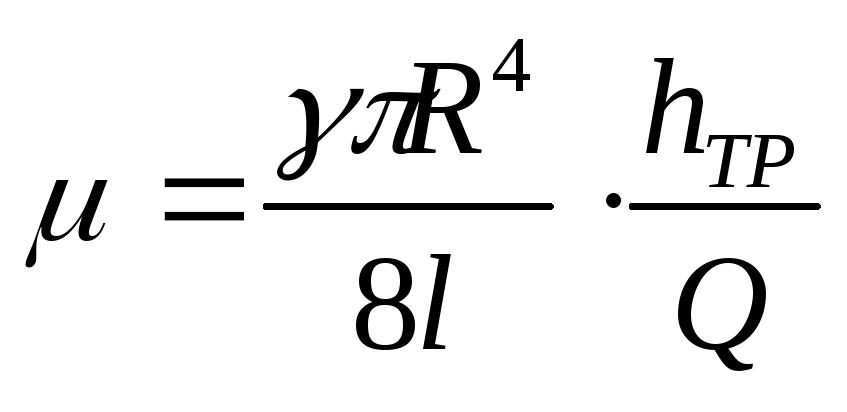
Рассчитанную по формуле (1) поправку алгебраически прибавляют к показаниям термометра.
7.2 Отобранную по ГОСТ 2517 пробу нефтепродукта подготавливают к проведению испытаний.
7.2.1 Нефтепродукты, содержащие твердые частицы, фильтруют через фильтр с отверстиями размером 75 мкм. При наличии в нефтепродукте воды его сушат безводным сульфатом натрия или прокаленной крупнокристаллической поваренной солью, или прокаленным хлористым кальцием и фильтруют через бумажный фильтр.
Примечание — Вязкие нефтепродукты допускается перед фильтрованием подогреть от 50°C до 100°C.
7.2.2 Остаточные цилиндровые масла, темные смазочные масла, остаточные котельные топлива (мазуты) и аналогичные парафинистые продукты, вязкость которых может быть обусловлена предыдущей тепловой обработкой, подготавливают в соответствии с 7.2.2.1-7.2.2.6.
7.2.2.1 Исследуемый образец нагревают в контейнере в течение 1 ч при температуре (60±2)°C тщательно перемешивая с помощью стержня до тех пор, пока не растворятся все парафиновые вещества.
Примечания
1 Для образцов с высоким содержанием парафинов или высокой вязкостью необходимо увеличить температуру нагрева выше 60°C. Образец должен быть жидким, чтобы его было удобно перемешивать.
2 Определение вязкости должно быть выполнено не позже чем через 1 ч после подогревания.
7.2.2.2 Контейнер плотно закрывают и энергично встряхивают в течение 1 мин.
7.2.2.3 Открывают контейнер и переливают 100 см исследуемого образца в стеклянную колбу.
7.2.2.4 Колбу неплотно закупоривают корковой или резиновой пробкой, и погружают на 30 мин в кипящую воду.
7.2.2.5 Вынимают колбу из кипящей воды, плотно закупоривают и встряхивают в течение 1 мин.
7.2.2.6 Фильтруют пробу в сушильном шкафу, не понижая температуры.
Примечание — Фильтр предварительно подогревают в сушильном шкафу до температуры испытания образца.
7.3 Из набора вискозиметров отбирают чистые сухие однотипные вискозиметры с пределами измерения, соответствующими ожидаемой вязкости испытуемого образца нефтепродукта и подготавливают их в соответствии с описанием работы с вискозиметрами, приведенным в приложении В.
Примечания
1 Для прозрачных жидкостей используют вискозиметры типов А и Б, для непрозрачных жидкостей используют вискозиметры типа В, приведенные в таблице А.1 (приложение А).
2 Диаметр капилляра вискозиметра должен обеспечивать время истечения не менее 200 с и не более 1000 с.
3 При температурах испытания ниже точки росы (температура, при которой образуется конденсат), на открытые колена вискозиметра надевают осушивающие трубки с наполнителем, чтобы предотвратить конденсацию воды из воздуха. Осушивающие трубки должны соответствовать конструкции вискозиметра и не должны препятствовать истечению исследуемого нефтепродукта под действием изменения давления в вискозиметре. Перед помещением вискозиметра в баню заполняют образцом рабочий капилляр и расширительную часть вискозиметра, сливают его еще раз в целях дополнительного предотвращения конденсации влаги или замерзания ее на стенках.
Перед помещением вискозиметра в баню заполняют образцом рабочий капилляр и расширительную часть вискозиметра, сливают его еще раз в целях дополнительного предотвращения конденсации влаги или замерзания ее на стенках.
8.1 Вискозиметр заполняют испытуемым нефтепродуктом в соответствии с описанием работы с вискозиметрами приведенным в приложении В. Наполненный вискозиметр помещают в термостат и закрепляют в держателе.
Примечания
1 При проведении определения вязкости прозрачного нефтепродукта заполняют и помещают в термостат один вискозиметр, при проведении определения вязкости непрозрачного нефтепродукта заполняют и помещают в термостат сразу два однотипных вискозиметра.
2 При проведении определения вязкости нефтепродукта, подготовленного в соответствии с 7.2.2.1-7.2.2.6, вискозиметры перед заполнением предварительно подогревают в сушильном шкафу до температуры испытания.
Вискозиметр закрепляют таким образом, чтобы капилляры были расположены вертикально, за исключением таких типов вискозиметров, для которых установлено другое положение. Вертикальность оценивают с помощью отвеса по верхней половине широкого колена вискозиметра. Величина отклонения оценивается на глаз.
Вертикальность оценивают с помощью отвеса по верхней половине широкого колена вискозиметра. Величина отклонения оценивается на глаз.
Примечания
1 Уровень нефтепродукта, находящегося в вискозиметре, должен быть не менее чем на 20 мм ниже уровня жидкости в термостате.
2 Для вискозиметров, у которых верхняя метка расположена непосредственно над нижней, отклонение от вертикали по всем направлениям не должно превышать 1°. Для вискозиметров, у которых верхняя метка отклонена относительно нижней, отклонение от вертикали по всем направлениям не должно превышать 0,3°.
8.2 Вискозиметр термостатируют в течение времени, указанном в приложении В для конкретного типа вискозиметра. По истечении 10 мин термостатирования доводят объем нефтепродукта до требуемого уровня, если этого требует конструкция вискозиметра.
Примечания
1 Если время термостатирования в приложение Б не указано, то вискозиметр термостатируют 30 мин. Для высоковязких нефтепродуктов время термостатирования необходимо увеличить.
Для высоковязких нефтепродуктов время термостатирования необходимо увеличить.
2 Погружать в термостат или вынимать из термостата вискозиметры или термометры, в то время когда хотя бы один вискозиметр находится в рабочем состоянии (во время измерения времени истечения), не допускается.
8.3 Используя подсос (если образец не содержит летучих веществ) или давление, устанавливают высоту столбика нефтепродукта в капилляре вискозиметра до уровня, находящегося приблизительно на 7 мм выше первой метки, если в инструкции по эксплуатации вискозиметра не установлено другое значение. При этом необходимо следить, чтобы в нефтепродукте не образовались пузырьки воздуха.
При свободном течении нефтепродукта через капилляр определяют время истечения (время перемещения мениска жидкости между метками, для которых определена постоянная вискозиметра).
Записывают значение времени истечения нефтепродукта с точностью до 0,1 с, температуру испытания (с учетом всех поправок) — до 0,01°C.
Примечания
1 При наличии возможности, показания термометров рекомендуется рассматривать с помощью оптических устройств, дающих примерно пятикратное увеличение, установленных так, чтобы исключить ошибки углового смещения между видимым и реальным направлением изображения.
2 Если время истечения менее 200 с, подбирают вискозиметр с меньшим диаметром капилляра и повторяют определение.
При определении вязкости прозрачного нефтепродукта проводят два последовательных измерения времени истечения нефтепродукта через один вискозиметр. Если разность между двумя значениями времени истечения жидкости не превышает величины определяемости (см. 5.1), то рассчитывают среднее арифметическое значение измерений времени истечения, которое используется для вычисления кинематической вязкости по формуле (2). Если разность между двумя значениями времени истечения жидкости превышает величины определяемости (см. 5.1), то определение необходимо повторить после тщательной очистки и сушки вискозиметра и фильтрации образца.
При определении вязкости непрозрачного нефтепродукта проводят по одному измерению времени истечения через оба вискозиметра (два параллельных определения времени истечения нефтепродукта). По параллельным значениям времени истечения нефтепродукта рассчитывают два значения кинематической вязкости по формуле (2). По двум значениям кинематической вязкости рассчитывают среднее значение кинематической вязкости.
Для остаточных котельных топлив (мазутов), рассчитывают разность между двумя значениями кинематической вязкости, если разность между двумя значениями не превышает величины повторяемости (см. 5.2), то рассчитывают среднее арифметическое значение кинематической вязкости, в противном случае операции необходимо повторить после тщательной очистки и сушки вискозиметра и фильтрации образца.
Примечание — Для других непрозрачных нефтепродуктов данные показатели точности не применяют.
9.1 Кинематическую вязкость , мм/с, вычисляют по формуле
, (2)
где — постоянная вискозиметра, мм/с;
— время истечения, с;
— ускорение свободного падения в месте определения кинематической вязкости, м/с;
— нормальное ускорение свободного падения (9,80665), м/с;
— поправка на кинетическую энергию, мм/с.
Ускорение свободного падения в месте определения кинематической вязкости, , м/с, вычисляют по формуле
=9,780318 (1+0,0053024 sin-0,0000059 sin 2)-2·10, (3)
где — географическая широта места, градус;
— высота над уровнем моря, м.
Примечания
1 Если ускорение свободного падения отличается от не более чем на 0,1%, то при расчете кинематической вязкости по формуле (2) отношение () можно принять равным единице.
2 Поправку на кинетическую энергию учитывают только в случаях определения кинематической вязкости менее 10 мм/с или времени истечения менее 200 с, в остальных случаях поправка на кинетическую энергию пренебрежительно мала и ее принимают равной нулю.
, (4)
где — коэффициент кинетической энергии, мм·с.
Коэффициент кинетической энергии , мм·с, вычисляют по формуле
, (5)
где — вместимость измерительного резервуара, мм;
— длина капилляра, мм;
— диаметр капилляра, мм.
9.2 Динамическую вязкость , мПа·с, вычисляют по формуле
, (6)
где — кинематическая вязкость нефтепродукта при температуре испытания, мм/с;
— плотность нефтепродукта при той же температуре, при которой определялась кинематическая вязкость, кг/м.
Примечание — Плотность нефтепродукта определяют по ГОСТ 3900.
Рассчитанное значение кинематической и/или динамической вязкости нефтепродукта округляют до 0,01% измеренной или расчетной величины, и записывают в протокол испытаний, указывая температуру испытания.
Протокол испытания должен содержать:
1) тип и марку испытуемого продукта;
2) ссылку на настоящий стандарт;
3) результаты испытаний;
4) любые отклонения, по соглашению или другим документам, от предписанной процедуры испытания;
5) дату проведения испытаний;
6) наименование испытательной лаборатории.
Примечание — При наличии разногласий испытания проводят без отступления от настоящего стандарта.
11.1 Между проведениями измерений вискозиметр тщательно промывают несколько раз растворителем, полностью смешивающимся с исследуемым нефтепродуктом, затем промывают осушающим растворителем, полностью испаряющимся и смешивающимся как с растворителем для нефтепродукта, так и с водой. Сушат вискозиметр, пропуская через него слабую струю чистого сухого воздуха в течение 2 мин или до полного удаления следов растворителя.
Примечания
1 Для большинства образцов в качестве растворителя, полностью смешивающегося с образцом, применяют петролейный эфир или нефрас. Вискозиметр после испытания остаточных котельных топлив (мазутов) необходимо предварительно промыть толуолом по ГОСТ 5789 или толуолом нефтяным по ГОСТ 14710, или ксилолом, чтобы удалить асфальтеновые вещества. В качестве осушающего растворителя, как правило, применяют ацетон.
2 Перед применением растворители следует отфильтровать.
11.2 Вискозиметр периодически промывают хромовой смесью или сильно окисляющей кислотой (отмачивают несколько часов, соблюдая меры предосторожности (см. 6.18), чтобы удалить остаточные следы органических отложений, затем тщательно ополаскивают последовательно дистиллированной водой и ацетоном, и сушат чистым сухим воздухом. Отложения неорганических веществ удаляют соляной кислотой перед промывкой хромовой смесью, особенно если предполагается присутствие солей бария.
Примечания
1 Применение щелочных очищающих растворов не допускается.
2 Перед применением воду и ацетон следует отфильтровать.
Контроль точности проводят в условиях испытательной лаборатории по указанной в стандарте процедуре измерений, используя утвержденные в установленном порядке стандартные образцы вязкости. Если разность измеренной кинематической вязкости стандартного образца вязкости и значения, приведенного в сертификате на него, превышает ±0,35%, необходимо проверить каждый этап испытания для выявления причины ошибок.
Примечание — Самыми частыми причинами ошибок являются следы отложений нефтепродуктов в отверстии капилляра и погрешность в измерении температуры. Правильный результат, полученный на сертифицированном стандартном образце, не исключает возможных источников ошибок.
Приложение А
(обязательное)
Типы капиллярных вискозиметров, обычно применяемых для определения вязкости нефтепродуктов, приведены в таблице А.1. Спецификации и инструкции по эксплуатации капиллярных вискозиметров приведены в [1].
Таблица А.1
Тип вискозиметра | Наименование вискозиметра | Диапазон измерения кинематической вязкости набором вискозиметров, мм/с |
Для прозрачных жидкостей | ||
А | Каннон-Фенске обычный | 0,5-20000 |
Цайтфукс | 0,6-3000 | |
BS с U-образной трубкой | 0,9-10000 | |
BS/U/M-миниатюрный | 0,2-100 | |
SIL | 0,6-10000 | |
Каннон-Маннинг, полумикро | 0,4-20000 | |
Пинкевич | 0,6-17000 | |
ВПЖ-4, ВПЖТ (ГОСТ 10028) | 0,6-10000 | |
ВПЖ-2, ВПЖТ-2 (ГОСТ 10028) | 0,6-10000 | |
Б | BS/IP/SL | 3,5-100000 |
BS/IP/SL (S) | 1,05-10000 | |
BS/IP/MSL | 0,6-3000 | |
Убеллоде | 0,3-100000 | |
Фитцсиманс | 0,6-1200 | |
Атлантик | 0,75-5000 | |
Каннон-Убеллоде (А), Каннон-Убеллоде с разбавлением (В) | 0,5-100000 | |
Каннон-Убеллоде, полумикро | 0,4-20000 | |
ДИН Убеллоде | 0,35-50000 | |
ВПЖ-1 (ВПЖТ-1) (ГОСТ 10028) | 0,6-30000 | |
Для прозрачных и непрозрачных жидкостей | ||
В | Канон-Фенске-Опакв — для непрозрачных жидкостей | 0,4-20000 |
Цайтфукс с перекрещивающимися трубками | 0,6-100000 | |
BS/IP/RF с U-образной трубкой с обратным истечением | 0,6-300000 | |
Ланц-Цайтфукс с обратным истечением | 60-100000 | |
ВНЖ, ВНЖТ (ГОСТ 10028) | 0,6-30000 | |
Каждый диапазон кинематической вязкости требует набора вискозиметров. Во избежание необходимости введения поправок на кинематическую энергию эти вискозиметры сконструированы таким образом, чтобы обеспечить время истечения более 200 с. Для данных вискозиметров с минимальной постоянной время истечения превышает 200 с. | ||
Приложение Б
(обязательное)
Б.1 Конструкция термометров и спецификация
Применяют специальные термометры с небольшим диапазоном измерения, соответствующим общей спецификации, приведенной в таблице Б.1, и по конструкции соответствующим чертежу, представленному на рисунке Б.1.
В таблице Б.2 приведены термометры ASTM, IP и ASTM/IP, соответствующие спецификации, изложенной в таблице Б.1, и температурам испытания.
Примечание — Разница в конструкции, главным образом, основывается на положении точки замерзания воды. В модели «a» точка замерзания воды находится в диапазоне шкалы, в модели «b» — ниже диапазона шкалы, в модели «c» — выше диапазона шкалы (см. рисунок Б.1).
Рисунок Б.1 Различные конструкции термометров
В таблице Б.1 приведены технические требования к термометрам, а также разъяснения к буквенным обозначениям чертежа, представленному на рисунке Б.1.
Таблица Б.1 — Технические требования к термометрам
Наименование параметра | Характеристика параметра |
Глубина погружения Разбиение шкалы: | Полная |
— цена самого малого деления, °С | 0,05 |
— цена длинного деления, °С | 0,1 и 0,5 |
Цифровые обозначения через каждые, °С | 1 |
Максимальная ширина деления, мм | 0,1 |
Погрешность шкалы при температуре испытания, °С, не более | 0,1 |
Камера расширения допускает нагревание до °С | 105 для шкалы термометра до 90 120 между 90-95 130 между 95-105 и 170 выше 105 |
Общая длина B, мм | 300-310 |
Наружный диаметр корпуса C, мм | 6,0-8,0 |
Длина ртутного резервуара D, мм | 45-55 |
Наружный диаметр ртутного резервуара E, мм | Не более чем наружный диаметр корпуса |
Длина шкалы G, мм | 40-90 |
Таблица Б.2 — Соответствие термометров по ГОСТ 400 термометрам по спецификациям ASTM и IP
Тип термометра по нормативной документации | Температура испытания, °C | ||
ГОСТ 400 | ASTM | IP | |
— | ASTM 74C | IP 69C | -53,9 |
ТИН 10-6 | ASTM 73C | IP 68C | -40,0 |
— | ASTM 126C | IP 71C | -26,1 |
— | ASTM 127C | IP 99C | -20,0 |
ТИН 10-10 | ASTM 72C | IP 67C | -17,8 |
ТИН 10-5 | ASTM 128C | IP 33C | 0,0 |
ТИН 10-1 | ASTM 44C | IP 29C | 20,0 |
ТИН 10-7 | ASTM 45C | IP 30C | 25,0 |
— | ASTM 118C | — | 30,0 |
ТИН 10-2 | ASTM 28C | IP 31C | 37,8 |
ТИН 10-8 | ASTM 120C | IP 92C | 40,0 |
ТИН 10-3 | ASTM 46C | IP 66C | 50,0 |
— | ASTM 29C | IP 34C | 54,4 |
ТИН 10-9 | ASTM 47C | IP 35C | 60,0 |
— | — | IP 100C | 80,0 |
— | ASTM 48C | IP 90C | 82,2 |
— | ASTM 129C | IP 36C | 93,3 |
ТИН 10-4 | ASTM 122C | IP 32C | 98,9 и 100,0 |
ТИН 10-4 | ASTM 121С | — | 100,0 |
— | ASTM 110 | IP 93C | 135,0 |
Приложение B
(справочное)
B.1 Вискозиметр типа Канон-Фенске (см. рисунок B.1).
На трубку 2 надевают резиновую трубку, конец трубки 1 погружают в сосуд с нефтепродуктом и засасывают нефтепродукт (с помощью резиновой груши, водоструйного насоса или другим способом) до метки , при этом необходимо следить, чтобы в жидкости не образовались пузырьки воздуха. В момент, когда уровень жидкости достигает метки , вискозиметр вынимают из сосуда и быстро устанавливают в нормальное положение. Снимают с внешней стороны конца трубки 1 избыток жидкости и надевают на этот конец резиновую трубку. Вискозиметр помещают в термостат и выдерживают в нем 30 мин. Расширение 3 должно находиться ниже уровня жидкости в термостате. После выдержки в термостате жидкость засасывают в расширение 4 приблизительно на 3 мм выше метки . Определяют время перемещения мениска жидкости от метки до метки .
B.2 Вискозиметр типа Пинкевича (ВПЖ-4, ВПЖТ-4 и ВПЖ-2, ВПЖТ-2), (см. рисунки B.2.1 и B.2.2).
На отводную трубку 3 надевают резиновую трубку. Далее, зажав пальцем конец трубки 2 и перевернув вискозиметр, опускают конец трубки 1 в сосуд с нефтепродуктом и засасывают его (с помощью резиновой груши, водоструйного насоса или иным способом) до метки , следя за тем, чтобы в жидкости не образовались пузырьки воздуха. В момент, когда уровень жидкости достигает метки , вискозиметр вынимают из сосуда и быстро перевертывают в нормальное положение. Снимают с внешней стороны конца трубки 1 избыток жидкости и надевают на него резиновую трубку. Вискозиметр устанавливают в термостат так, чтобы расширение 4 было ниже уровня жидкости. После выдержки в термостате не менее 15 мин засасывают жидкость в трубку 1 примерно до 1/3 высоты расширения 4. Определяют время перемещения мениска жидкости от метки до .
Рисунок B.1 — Вискозиметр типа Канон-Фенске | Рисунок B.2.1 — Вискозиметр типа Пинкевича (ВПЖТ-4, ВПЖ-4) | Рисунок B.2.2 — Вискозиметр типов ВПЖТ-2, ВПЖ-2 |
B.3 Вискозиметры типов ВПЖТ-1, ВПЖ-1 (БС/ИП/СЛ) (см. рисунок B.3).
Испытуемый нефтепродукт наливают в чистый вискозиметр через трубку 1 так, чтобы уровень ее установился между метками и 2 и 3 надевают резиновые трубки, при этом первая из них должна быть снабжена краном, вторая — краном и резиновой грушей. Вискозиметр устанавливают вертикально в жидкостном термостате так, чтобы уровень термостатирующей жидкости находился на несколько сантиметров выше расширения 4. При температуре испытания вискозиметр выдерживают не менее 15 мин, после чего всасывают (грушей) при закрытой трубке 2 жидкость выше метки примерно до середины расширения 4 и перекрывают кран, соединенный с трубкой 3. Если вязкость нефтепродукта менее 500 сСт, открывают кран на трубке 3 и потом освобождают зажим на трубке 2. При более вязких нефтепродуктах сначала открывают трубку 2, затем трубку 3. Далее измеряют время перемещения мениска жидкости в трубке 2 от метки до . Необходимо при этом обращать внимание на то, чтобы к моменту подхода уровня жидкости к метке в расширении 5 образовался «висячий уровень», а в капилляре не было пузырьков воздуха.
B.4 Вискозиметр типа Убеллоде (см. рисунок B.4)
В чистый сухой вискозиметр вносят пробу нефтепродукта следующим образом. Вискозиметр отклоняют на 30° от вертикального положения так, чтобы сосуд 7 оказался под капилляром. С помощью заполнительной трубки 1 вносят пробу так, чтобы ее уровень достиг нижней метки . Потом вискозиметр возвращают в нормальное положение, следя за тем, чтобы уровень жидкости не превышал верхней метки . При заполнении вискозиметра пробой в жидкости не должны образовываться пузырьки воздуха. Вискозиметр с пробой помещают в термостат. Через 20 мин выдержки на трубку 3 надевают резиновую трубку, трубку 2 закрывают пальцем и пробу засасывают до половины расширения 4. Потом трубку 2 открывают, ждут, пока проба перетечет из трубки 2 в сосуд 6 и образуется «висячий уровень». Освобождают трубку 3 и измеряют время перемещения мениска жидкости от метки до .
B.5 Вискозиметры типов ВНЖ, ВНЖТ (Канон-Фенске-Опакв) (см. рисунок B.5)
На отводную трубку 3 надевают резиновую трубку. Зажав пальцем конец трубки 2, и перевернув вискозиметр, опускают конец трубки 1 в сосуд с нефтепродуктом и засасывают его (с помощью резиновой груши, водоструйного насоса или иным способом) до метки M, вискозиметр вынимают из сосуда и быстро перевертывают в нормальное положение. Снимают с внешней стороны конца трубки 1 избыток нефтепродукта и надевают кусочек резиновой трубки длиной 8-15 см с присоединенным закрытым краном или зажимом. Затем открывают кран для заполнения жидкостью резервуара 6 и вновь его закрывают, когда жидкость заполнит приблизительно половину резервуара 6. Вискозиметр устанавливают в термостат и после необходимой выдержки в нем (20 мин) открывают трубку 1 и, пользуясь двумя секундомерами, измеряют время течения жидкости от метки до и от метки до . По измеренному времени заполнения резервуара 5 вычисляют вязкость. Измеренное время заполнения резервуара 4 служит для контроля. Значения вязкости, вычисленные по времени заполнения резервуаров 5 и 4, могут отличаться до 2%, а при температуре ниже 15°C — до 3%.
|
|
|
B.6 Вискозиметр типа БС/ИП/РФ (см. рисунок B.6).
Вискозиметр помещают в термостат так, чтобы верхняя метка 1 пробу (проба может быть подогретой), следя за тем, чтобы не намочить стенки вискозиметра над меткой , закрывают трубку 2 и останавливают течение жидкости. Пробу доливают до метки 2 и доводят уровень пробы до метки . Трубку 2 снова закрывают. С помощью пипетки с предохранительным упором устанавливают пробу над меткой 1 и соприкосновении упора с краем трубки 1 конец пипетки был точно на метке
К пипетке присоединяют отсос и осторожно отсасывают избыток пробы, пока пипетка не начнет всасывать воздух, после чего пипетку вынимают. Потом трубку 2 освобождают и измеряют время прохождения мениска жидкости от метки до .
С одним заполнением вискозиметра производят только одно измерение времени течения.
Рисунок В.6 — Вискозиметр типа БС/ИП/РФ с U-образной трубкой
[1] | ISO 3105:1994* | Glass capillary kinematic viscometers — Specifications and operating instructions (Вискозиметры стеклянные капиллярные для определения кинематической вязкости. Технические требования и инструкция по эксплуатации) |
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. — Примечание изготовителя базы данных.
УДК 665.6:532.13:006.354 | МКС 75.080 |
Ключевые слова: определение вязкости нефтепродуктов, кинематическая вязкость, динамическая вязкость, ньютоновские жидкости | |
Искусственное завышение вязкости улучшает сходимость задач вычислительной гидродинамики
Приходилось ли Вам моделировать турбулентные течения при решении задач вычислительной гидродинамики? Тогда вы наверняка знаете, что выполнение расчета иногда занимает довольно много времени по причине сложностей, возникающих при поиске численного решения. Эти сложности обусловлены нелинейностью уравнений, описывающих турбулентные потоки. Сократить время расчета можно, если сначала решить задачу с искусственно завышенным значением коэффициента вязкости жидкости, а затем использовать полученное решение в качестве начального приближения для задачи с более низким значением вязкости. Мы покажем вам, как реализовать указанный подход в среде COMSOL Multiphysics.
Почему искусственное завышение вязкости улучшает сходимость задач вычислительной гидродинамики?
Прежде чем приступать к моделированию течения жидкости, нужно рассчитать число Рейнольдса, характеризующее это течение. Число Рейнольдса по определению равно:
Re = \frac{\rho U d}{\mu}
Здесь \rho — плотность движущейся среды, а \mu — динамический коэффициент вязкости, U — характерная скорость, d — характерный линейный размер системы.
Число Рейнольдса характеризует отношение сил инерции и вязкости, действующих в потоке. Зная число Рейнольдса, можно определить, какой режим течения — ламинарный или турбулентный — мы должны моделировать в COMSOL Multiphysics. Например, в микроканале, где характерная скорость и линейный размер относительно невелики, значение число Рейнольдса мало, а значит режим течения ламинарный. Обратный пример — движение автомобиля с высокой скоростью. В этом случае течение характеризуется высоким значением числа Рейнольдса, следовательно, режим течения турбулентный. В одной из предыдущих статей блога мы более подробно рассказывали об определении режима течения.
Найти численное решение задачи о турбулентном течении, как правило, сложнее, чем в случае ламинарного потока. Чтобы понять, почему, давайте обратимся к уравнениям, описывающим поле течения. В COMSOL Multiphysics турбулентные течения описываются осрдненными по Рейнольдсу уравнениями Навье-Стокса (RANS). В уравнения RANS вводится новая переменная, получившая название турбулентной вязкости, которая характеризует степень турбулентности потока. Турбулентная вязкость рассчитывается с использованием дополнительных уравнений, вид которых определяется используемой моделью турбулентности.
Например, для расчета турбулентной вязкости в k-epsilon модели турбулентности используются величины кинетической энергии турбулентности (k) и турбулентной диссипации (epsilon). Уравнения модели турбулентности по форме похожи на уравнения Навье-Стокса и тоже содержат линейные и нелинейные члены. Нелинейность уравнений турбулентности объясняет, почему при высоких числах Рейнольдса гораздо сложнее добиться сходимости задачи. Узнать, как выбрать модель турбулентности, вы можете из этой статьи в блоге.
Таким образом, для моделирования течений при больших числах Рейнольдса мы должны использовать модели турбулентности, и уравнения, которые решает COMSOL Multiphysics в этом случае, становятся сильно нелинейными. Использование хороших начальных приближений может улучшить сходимость нелинейных задач, как описано здесь. Степень нелинейности уравнений определяется вязкостью жидкости. Если сначала задать в параметрах модели высокое значения коэффициента вязкости, то тогда мы сможем решить слабо нелинейную задачу, которая лучше сходится. Затем мы сможем использовать полученное решение в качестве хорошего начального приближения для жидкости с более низкой вязкостью. Таким образом, мы повысим сходимость той задачи, которую хотим решить. Этот подход называется методом завышения вязкости.
В рамках этого подхода задача решается последовательно, при этом сначала вязкость жидкости искусственно завышается, а затем постепенно снижается, пока не достигнет заданного значения. Решение задачи, полученное при завышенной вязкости, используется в качестве начального приближения для следующего шага с меньшей вязкостью. Сначала мы решаем задачу с более высокой вязкостью, снижая таким образом числом Рейнольдса. То есть мы начинаем с решения слабо нелинейной задачи, которая лучше сходится. Уменьшая вязкость (и тем самым увеличивая число Рейнольдса) до заданного значения, мы переходим от слабо нелинейной задачи к сильно нелинейной, и в конце этой процедуры мы получаем решение исходной задачи. Давайте теперь посмотрим, как этот подход можно реализовать в COMSOL Multiphysics.
Реализация метода искусственного завышения вязкости в COMSOL Multiphysics
Давайте предположим, что вы уже построили CFD-модель в COMSOL Multiphysics и теперь хотите улучшить ее сходимость. Метод завышения вязкости состоит из трех этапов.
- Задание повышающего параметра
- Умножение коэффициента вязкости на повышающий параметр
- Настройка параметрического исследования
Сначала нужно задать новый параметр, на который мы будем умножать коэффициент вязкости. Значение, которое мы установили для «visc_ramp» в узле Parameters не важно, так как позже мы зададим его через настройку параметрического исследования (auxiliary sweep).
Задаем параметр.
Затем перейдем к узлу Materials и умножим коэффициент вязкости на параметр «visc_ramp». Например, если «visc_ramp» имеет значение 100, расчет будет выполнен для жидкости, имеющей в 100 раз более высокий коэффициент вязкости, чем задано по условию задачи. В конечном итоге, когда значение «visc_ramp» достигнет 1, коэффициент вязкости жидкости вернется к своему фактическому значению.
Умножаем коэффициент вязкости на параметр «visc_ramp».
В настройках стационарного решателя мы задаем значения варьируемого параметра «visc_ramp», равные 1000, 100, 10 и 1. После запуска параметрического исследования сначала будет рассчитано решение для первого значения параметра «visc_ramp» (1000), которое затем автоматически будет использовано в качестве начального приближения для поиска решения при следующем значении параметра «visc_ramp» (100). Параметрическое исследование завершится, когда параметр «visc_ramp» станет равен 1, то есть когда будет найдено решение для фактической вязкости жидкости.
Настройка стационарного решателя.
В процессе выполнения расчета на вкладке Progress отображается текущее значение параметра «visc_ramp». В итоге сходимость достигнута, и мы можем посмотреть результаты.
Вкладка Progress со значением параметра «visc_ramp», равным 100.
Описанная процедура искусственного завышения вязкости проиллюстрирована ниже. На рисунке показаны линии тока и поле скорости турбулентного потока за обратным уступом, рассчитанные с помощью модели из Галереи приложений.
Линии тока и поле скорости при турбулентном течении в канале с обратным уступом для трех разных коэффициентов вязкости.
Выбор параметра при настройке параметрического исследования
Чаще всего в качестве начального значения повышающего параметра для достижения сходимости достаточно задать 100 или 10. Однако в тех случаях, когда добиться сходимости труднее, рекомендуется использовать более высокое начальное значение повышающего параметра, а затем снижать его значение на порядок (например, 1000, 100, 10, 1).
В данном случае мы начали расчет поля течения для очень вязкой жидкости (1000), определили промежуточные значения «visc_ramp» (100 и 10), чтобы добиться сходимости при фактическом значении коэффициента вязкости жидкости («visc_ramp» = 1). Если не удается найти решение при следующем более низком значении вязкости, то автоматически будет сделана попытка получить решение при значении, лежащем между последним сошедшимся и следующим заданным пользователем значениями параметра. Этот метод известен как бектрекинг.
Чтобы продемонстрировать работу бектрекинга, давайте запустим параметрическое исследование, выбрав в качестве значений «visc_ramp» 1000 и 1. После того, как решение для повышающего параметра, равного 1000, найдено, программа попытается решить задачу при фактическом значении вязкости. Если решателю не удается получить сходящееся решение, тогда расчет повторяется для промежуточного значения параметра (в данном случае, 501). Когда решение для параметра, равного 501, получено, программа снова попытается решить задачу при фактическом значении вязкости (параметр завышения вязкости равен 1), и, на этот раз расчет завершится успешно!
Вкладка Progress со значением параметра «visc_ramp», равным 501.
Бектрекинг — это полезный встроенный алгоритм, используемый решателем для улучшения сходимости при проведении параметрических исследований. Тем не менее, пользователь должен указать промежуточные значения параметра, чтобы обеспечить более эффективный переход солвера от больших к меньшим значениям.
Иногда, несмотря на использование метода бектрекинга, решение перестает сходится при значении параметра больше 1. Как правило, это означает, что для расчета поля течения используется слишком грубая сетка. В этом случае начать надо с построения более плотной сетки. Кроме того, стоит помнить о необходимости исследования задачи на чувствительность к параметрам сетки. Такой анализ является неотъемлемой частью верификации полученных результатов.
Эффективность методов завышения вязкости и постепенного повышения нелинейности
Мы показали, как использовать искусственное завышение вязкости в COMSOL Multiphysics для улучшения сходимости задач вычислительной гидродинамики. Для этого мы настроили параметрическое исследование, начав решение с задачи со слабой нелинейностью, а затем постепенно повышали степень нелинейности до тех пор, пока не получили решение исходной задачи. Метод искусственного завышения вязкости довольно полезен при решении задач вычислительной гидродинамики, характеризующихся высокими значениями числа Рейнольдса, другими словами, при моделировании турбулентных течений.
Описанный способ снижения нелинейности может применяться в самых разных задачах. Например, вместо завышения вязкости мы можем постепенно увеличивать силу тяжести в задачах свободной конвекции или индекс текучести «n» при моделировании течения неньютоновских жидкостей. Описанная методика также может быть использована при решении самого широкого класса нелинейных мультифизических задач, о чем мы рассказываем в этой публикации.
Для достижения сходимости задачи мы можем также использовать метод постепенного повышения нагрузки. Повышение нагрузки применительно к течению жидкости, как правило, означает постепенное увеличение скорости на входе. Это еще один способ достижения сходимости, о котором не стоит забывать.
Хотите узнать больше об этих методах и их использовании при решении ваших собственных задач в COMSOL Multiphysics? Пожалуйста, свяжитесь с нами.
Коэффициент вязкости— обзор
11.11.2.4 Жидкостная смазка
Когда капля масла с плотностью ρ lq и коэффициентом вязкости μ lq движется к открытому отверстию капилляр из его первоначального прикрепленного положения на торце инструмента, разница в давлении в капилляре и выходе из него может толкать каплю в капилляр против движения стружки со скоростью V chip .Если испарением масла в капилляре можно пренебречь, скорость потока масла, v , будет распределена в форме потока Куэтта в продольном сечении капилляра следующим образом:
[5] v = 12μlq (ⅆpⅆξ) (η2 − h¯η) + Vchiph¯η − v0
, где η (0 <η
[6] v¯ = −112μlq (ⅆpⅆξ) h¯2 + 12Vchip − v0
Теперь можно предположить, что внутренняя часть капилляра практически сохраняется в вакууме абсолютного давления, p = 0. Также разумно предположить, что теплоноситель, проникающий в капилляр, приводится в движение только атмосферным давлением, p атом . Для простоты предположим, что v 0 = 0 и что капиллярное притяжение или поверхностное натяжение охлаждающей жидкости пренебрежимо мало, поскольку скорость стружки намного выше скорости проникновения охлаждающей жидкости из-за капиллярного действия.Пусть l l обозначает среднюю глубину проникновения теплоносителя в капилляр, тогда l l можно определить, приняв v¯ = 0 и d p / d ξ = p атом. / л л , а именно
[7] ll = 16 мклкпатомVchiph¯2
Это уравнение утверждает, что глубина проникновения жидкости, л л , будет увеличиваться с увеличением квадрата высоты капилляра, h ¯, аналогично глубине проникновения газа, l g , в потоке Кнудсена.Для капилляра на границе раздела между рабочей поверхностью износа по задней поверхности и обработанной поверхностью l l будет описано как
[8] ll = 16μlqpatomVch¯2
Соотношение между средней глубиной проникновения, l l , и скорость В микросхема или В c для h¯ = 1 мкм показаны на рисунке 16, а отношения между l l и h¯ для V чип = 0.607 мс — 1 (36,4 м мин. — 1 ) и В c = 1,67 мс — 1 (100 м мин. — 1 ) показаны на рисунке. 17. Обратите внимание, что коэффициент вязкости охлаждающей жидкости предполагается равным 1,1 × 10 −3 Па · с для охлаждающей жидкости на водной основе, включая эмульсионные, растворимые и растворимые ( 18 ) и 18,0 × 10 −3 Па. s для смазочно-охлаждающей жидкости MQL. Из этих диаграмм очевидно, что глубина проникновения смазочно-охлаждающей жидкости MQL будет значительно мала.Следовательно, жидкое масло при MQL-механической обработке не может хорошо смазывать область контакта стружки со стружкой или поверхность раздела между контактной площадкой для износа по задней поверхности и обработанной поверхностью, даже если на этих поверхностях образуется достаточное количество капилляров.
Рис. 16. Глубина проникновения СОЖ в капилляр h¯ = 1 мкм в зависимости от скорости стружки или скорости резания.
Рис. 17. Глубина проникновения СОЖ в капилляр в зависимости от высоты капилляра h¯ для В чип = 36.4 м мин. — 1 и V c = 100 м мин. — 1 .
Существует огромная разница в глубине проникновения в капилляр между газообразной и жидкой смазкой, как показано на рисунках 15 и 16. Это причина, по которой обработка MQL считается гораздо более предпочтительной для смазки стружки и инструмента. –Рабочие интерфейсы, чем обработка с заливным СОЖ. Обратите внимание на то, что сочетание капель масла и сжатого воздуха при обработке MQL не так эффективно для охлаждения инструмента и работы, как обычно происходит с охлаждающей жидкостью, но это не обязательно считается отрицательным фактором при чистовой токарной обработке с небольшой глубиной резания или при чистовом фрезеровании с малой осевой глубиной резания.При обработке MQL необходимо уменьшить термическое воздействие из-за прерывистого резания, как будет объяснено позже, и, таким образом, на режущей кромке не будет много термических трещин. В результате, несмотря на то, что капли масла и сжатый воздух не обладают достаточным охлаждающим эффектом, срок службы инструмента может быть значительно увеличен при обработке MQL.
Рисунок 17 показывает, что охлаждающая жидкость на водной основе с высокой проницаемостью может проникать глубже в капилляр, если обработка поверхности жесткая.Кроме того, если капля большая и, следовательно, требуется некоторое время для испарения, как показано на рисунке 11, тогда возникнет жидкофазная смазка, так как капля может проникнуть в капилляр до определенной степени до того, как ее испарение начнется в устье. капилляр.
Коэффициент вязкости — формула, единица СИ, единица измерения и размер
Вязкость определяется как отношение силы, необходимой для того, чтобы соседние слои жидкости перемещались друг над другом.
Рисунок.1 (а) показана идеальная или сверхтекучая жидкость без трения, однако практически всегда присутствует некоторое трение в жидкостях, как показано на рисунке. 1 (б).
Давайте возьмем пример,
Как вы можете видеть на рисунке 2 выше, в каждом горизонтальном слое жидкости есть вариации, которые происходят из-за наличия некоторого внутреннего трения (вязкости) между слоями жидкости. проходя через две пластины.
Коэффициент вязкости
Отношение напряжения сдвига к градиенту скорости жидкости называется коэффициентом вязкости η.
Следовательно, коэффициент вязкости определяется как
, где
F — тангенциальная сила, необходимая для поддержания единичного градиента скорости между двумя параллельными слоями жидкости единичной площади.
ⅴ — скорость.
A — площадь
d — расстояние между двумя слоями жидкости, скользящими друг по другу.
Разница в скорости потока между соседними слоями жидкости измеряется градиентом скорости.
В основном вязкость газа меньше вязкости жидкости.
SI Единица коэффициента вязкости
Каждая жидкость имеет свою удельную вязкость, и мера этого атрибута называется коэффициентом вязкости.
Коэффициент вязкости η определяется как тангенциальная сила F, необходимая для поддержания единичного градиента скорости между двумя параллельными слоями жидкости с единичной площадью A.
Единица измерения η в системе СИ — ньютон-секунда на квадратный метр (Нс.4/8 η l
Здесь скорость течения вязкой жидкости через трубку длиной l и радиусом пропорциональна приложенному давлению P.
Скорость потока вязкая жидкость пропорциональна четвертой степени внутреннего радиуса трубки и обратно пропорциональна вязкости жидкости и длине трубки. 4/8 Ⅴ l
Здесь
Ⅴ — скорость потока объема жидкости.2 или 0,890 сП.
Следовательно, вода имеет вязкость 0,0091 пуаз
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Коэффициент определения вязкости, формула, примеры, 2 типа
Жидкости имеют тенденцию течь. Некоторые жидкости менее вязкие, некоторые более вязкие. Мы видим, что мед течет медленнее, чем вода. Это из-за вязкости. Давайте больше узнаем о коэффициенте вязкости и его свойствах.
Вязкость
Вязкость маслаВязкость жидкости — это степень ее защиты от деформации при заданной скорости. Для жидкостей это можно сравнить со случайным понятием «вязкость»: например, сироп имеет более высокую вязкость, чем вода.
Вязкость можно отнести к категории измерения силы внутреннего трения, возникающей между двумя взаимодействующими слоями жидкости, находящимися в относительном движении.
Например, когда жидкость проходит через цилиндр, она течет с большей скоростью вблизи ступицы цилиндра, чем рядом с его разделителями.
В таком случае испытания показывают, что некоторое давление (например, взвешенный контраст между двумя поверхностями цилиндра), как ожидается, продолжит движение через цилиндр.
Это потому, что сила важна для преодоления эрозии между слоями жидкости, которые находятся в относительном движении: качество этой силы соответствует вязкости.
Жидкость, не имеющая защиты от сдвигового давления, называется идеальной или невязкой жидкостью. Нулевая вязкость отчетливо наблюдается при низких температурах в сверхтекучих жидкостях.
Что-то еще, второй закон термодинамики требует, чтобы все жидкости имели положительную вязкость; такие жидкости должны быть вязкими или вязкими.
Простое определение
В материаловедении и дизайне каждый стремится понять силы или напряжения, связанные с искажением материала.
Например, если бы материал был простой пружиной, соответствующий ответ дал бы закон Гука, который гласит, что сила, испытываемая пружиной, соответствует разъединению, вырванному из гармонии. Напряжения, которые могут быть приписаны деформации материала из некоторых расслабленных состояний, называются гибкими напряжениями.В различных материалах доступны напряжения, которые можно отнести к темпам развития обезображивания через некоторое время. Это называется тяжелой ношей.Например, в жидкости, вода, бремя, возникающее в результате сдвига жидкости, не зависит от разделения жидкости, которая была разрезана; скорее, они полагаются на скорость, с которой происходит срезание.
Вязкость — это свойство материала, которое связывает вязкое напряжение в материале со скоростью развития деформации (скоростью деформации).
Несмотря на то, что это применимо к обычным потокам, это совсем не сложно представить в простом срезанном потоке, например, в плоском потоке Куэтта.
Типы вязкости
Типы вязкостиЕсть два четких приближения вязкости, используемых для описания жидкостей, динамической и кинематической вязкости.
Они изображают развитие жидкости различными способами, которые определяются тем, как они оцениваются, в любом случае они совместимы, если известна вязкость жидкости.
Обычно используются два вида вязкости: уникальная вязкость μ и кинематическая вязкость ν.
Динамическая вязкость
Динамическая вязкость измеряет величину сдвига, связанного со скоростью сдвига для жидкости.
Динамическая вязкость отождествляется с кинематической вязкостью по условию μ = ρν, где ρ — вязкость жидкости.
Единица динамической вязкости μ — сантипуаз. Если вязкость жидкости ρ измеряется в г / куб.см, тогда кинематическая вязкость ν выражается в сантистоксах.
Следовательно, 1 сантисток повышается до 1 сантипуаз, изолируя 1 г / куб.
Кинематическая вязкость
Кинематическая вязкость измеряет соотношение вязкой и инерционной силы жидкости.
Кинематическую вязкость можно сравнить с коэффициентом диффузии массы и тепла, который является коэффициентом диффузии энергии.
Формула коэффициента вязкости
Формула коэффициента вязкости приведена ниже:
F / A = n (DV / DR)
, где F говорит с силой, а A говорит с областью.Таким образом, F / An, или степень, разделенная по площади, является еще одним методом определения вязкости. DV с изолированным DR указывает на «скорость сдвига» или скорость движения жидкости.
n — стабильная единица измерения, эквивалентная 0,00089 Па · с (Паскаль-секунда), которая является уникальной единицей оценки вязкости. У этого закона есть несколько важных жизнеспособных приложений, например, струйная печать, детали / настои белков и производство продуктов питания / напитков.
Коэффициент вязкости определяется как посторонняя мощность, необходимая для поддержания единичного наклона скорости между двумя равными слоями жидкости единичной области.
Численно
Коэффициент вязкости (η) = Fr / Av, где F = сторонняя мощность, r = расстояние между слоями, v = скорость.
Размерная формула силы = M¹L¹T-²Формула размеров для площади = MºL²Tº
Размерная формула расстояния = MºL¹Tº
Размерная формула скорости = MºL¹T-¹Помещая эти качества в указанное выше условие, получаем:
[η] = [M¹L¹T-²] [MºL¹Tº] / [MºL²Tº] [MºL¹T-¹] = [M¹L-1T-]
Размерная формула коэффициента вязкости (η) = [M¹L-¹T-¹]
Единица измерения СИ Коэффициент вязкости (η) — Паскаль-секунда.
Применения вязкости
Значение вязкости можно понять по прилагаемым моделям.
Масло в транспортных средствах
Масло в транспортных средствахКогда вы заливаете масло в свой автомобиль или грузовик, вы должны знать его вязкость. Это связано с тем, что вязкость влияет на решетку, а эрозия, таким образом, влияет на нагрев.
Более того, вязкость дополнительно влияет на скорость использования масла и простоту, с которой ваш автомобиль начнет движение в жарких или холодных условиях.
Некоторые масла имеют более стабильную вязкость, в то время как другие реагируют на тепло или холод; Если список вязкости вашего масла невелик, оно может стать более тонким по мере нагревания, что может вызвать проблемы, когда вы работаете на своем автомобиле в жаркий летний день.
Кулинария
CookingВязкость предполагает значительную работу по приготовлению и подаче пищи. Кулинарные масла могут изменять вязкость при нагревании, в то время как многие из них становятся значительно более вязкими при охлаждении.
Жиры, которые при нагревании являются относительно вязкими, при охлаждении становятся твердыми.Различные стили приготовления дополнительно зависят от вязкости соусов, супов и рагу. Густой суп из картофеля и лука-порея, например, когда он менее вязкий, становится французским вишисуазом.
Некоторые вязкие жидкости добавляют поверхности питательным веществам; нектар, например, очень густой и может изменить «ощущение во рту» блюда.
Сборка
СборкаСборка оборудования требует надлежащего масла для нормальной работы. Слишком густые масла могут прилипать и закупоривать трубопроводы.Слишком скудные мази плохо защищают движущиеся части.
Лекарства
Medication — Gel MedicineВязкость может иметь решающее значение при приеме лекарств, поскольку жидкости попадают в организм внутривенно.
Вязкость крови — серьезная проблема: слишком вязкая кровь может образовывать опасные внутренние скопления, в то время как слишком нежная кровь не образует комков; это может привести к опасным кровавым несчастьям и даже к гибели.
Вся наука — это не что иное, как утонченное повседневное мышление, цитируемое известным ученым Альбертом Эйнштейном.Наука объясняет все возможные явления. Вязкость — это не явление, а скорее привычный характер жидкостей, определяющий их текучесть.
Читайте также:
Магическое число — Ядерная химия и радиоактивность
Факторы, влияющие на трение — необходимое зло
Refraction — Факты, типы и примеры
Выбор масел с высоким коэффициентом вязкости
Являются ли синтетические масла (PAO — полиальфаолефин и PAG — полиалкиленгликоль) лучшими смазочными материалами для редукторов и подшипников, чем минеральные масла?
В основе проблемы лежит свойство, которое мы называем коэффициентом вязкости под давлением различных типов базовых масел.
Коэффициент вязкости давления относится к соотношению между нагрузкой на масляную пленку (давлением) в зоне динамической нагрузки и толщиной масляной пленки (вязкостью) при этой нагрузке, когда все другие факторы (материал, температура, геометрия, скорость, нагрузка) постоянны.
Коэффициент давление-вязкость дает нам фиксированные значения толщины смазочной пленки в заданном наборе условий (эластогидродинамический режим, также известный как режим EHL или EHD) на основе математической оценки, как указано в Информационном листе Американской ассоциации производителей зубчатых передач (AGMA). AGMA 925-A03 (см. Примечание).
Фактическая единица измерения (мм 2 / Н) менее полезна, чем процентное улучшение синтетического масла по сравнению с минеральным маслом при заданных температурах, как указано в информационном листе.
Анализ показывает, что на самом деле существуют условия, при которых минеральное масло превосходит синтетические PAO / PAG. В частности, обратите внимание на сравнение уровней производительности для температур ниже 80 ° C.
Однако по мере изменения температуры соотношение меняется, оставляя нам четкое указание на то, когда мы можем ожидать увидеть, какие синтетические материалы демонстрируют превосходную пленкообразующую способность в определенном температурном диапазоне.
Многое известно о потенциальной пользе синтетических материалов для энергосбережения. Надеюсь, эти данные дают представление о том, когда и почему мы вправе ожидать снижения условий трения, что приведет к повышению надежности и экономии энергии в результате перехода на смазку на синтетической основе.
Ясно, что не всегда лучше использовать синтетическую смазку.
Примечание технического редактора
Исследование, сравнивающее толщину пленки EHL иЗдесь представлена температура для минеральных смазок, смазочных материалов на основе полиальфаолефинов и полиалкиленгликолей. Цель состоит в том, чтобы определить, как смазка ch58ce может повлиять на расчет срока службы подшипников.
Методы измерения для определения коэффициента вязкости-давления
Толщина пленки EHL была рассчитана с использованием уравнений из AGMA 925. 1 Коэффициент вязкости давления определяет количественно способность смазки к образованию пленки EHL.
Коэффициент «давление-вязкость» измеряется либо непосредственно путем оценки вязкости как функции давления с использованием аппарата высокого давления, либо косвенно путем измерения толщины пленки в оптическом интерферометре.В последнем случае коэффициент вязкости давления рассчитывается по измеренной толщине пленки с использованием уравнения толщины пленки EHL.
Хотя прямые измерения могут быть более точными, они недоступны. AGMA 925-A03 дает коэффициенты вязкости и давления, полученные на основе оптической интерферометрии, для многих смазочных материалов в широком диапазоне температур.
Уравнение толщины пленки — это уравнение Доусона и Тойоды для центральной толщины пленки. Это относится к компонентам с линейным контактом, таким как шестерни и роликовые подшипники.
Смазочные материалы
В таблице 1 приведены значения абсолютной вязкости и коэффициента вязкости под давлением, полученные для AGMA 925. 1
Таблица 1. Абсолютная вязкость и вязкость при давлении
Коэффициент в зависимости от температуры
Температура
Толщина пленки EHL определяется рабочей температурой компонентов. Для шестерен важна температура зубьев шестерни. Для подшипников важна температура внутреннего кольца и роликов.Типичная рабочая температура боковой поверхности шестерни, кольца подшипника и ролика составляет 80 ° C. Факторы окружающей среды могут влиять на фактическую рабочую температуру.
Толщина пленки EHL
Толщина пленки EHL была рассчитана с использованием уравнения 65 из AGMA 925 1 :
где
- Hc — безразмерная центральная толщина пленки
- G — параметр материалов
- U — параметр скорости
- W — параметр нагрузки
Если геометрия, упругие свойства, скорость и нагрузка фиксированы, толщина пленки EHL изменяется в зависимости от коэффициента вязкости давления () и абсолютной вязкости (), как показано в уравнении No.2:
Нормализованная толщина пленки EHL
Толщина пленки EHL была нормализована путем деления уравнения № 2 на свойства минерального масла при 80 ° C, как показано в уравнении № 3: температура 80 ° C является типичной для рабочей температуры зубьев шестерни, внутреннего кольца и роликов. подшипников качения.
Уравнение № 3 нормализует толщину пленки к толщине пленки минерального масла при 80 ° C, чтобы позволить прямое сравнение толщины пленки, достигаемой синтетическими смазочными материалами PAO и PAG, с толщиной пленки, достигаемой минеральным маслом.
В таблице 2 и на рисунке 3 приведены нормализованные значения толщины пленки, рассчитанные с использованием уравнения № 3 (см. Примечание).
Обсуждение
На рис. 1 показана зависимость абсолютной вязкости от температуры для минеральных, полиальфаолефиновых и полиальфаолефиновых смазок.
На рис. 2 показана кривая коэффициента вязкости и давления для минерального масла, которая выше и круче, чем кривые для смазок на основе PAO и PAG, в диапазоне температур.
На рисунке 3 показано, что синтетические смазочные материалы на основе ПАО и ПАА имеют схожие тенденции изменения толщины пленки EHL при изменении температуры.Смазка PAG дает более толстые пленки, чем смазка PAO при всех температурах. Минеральное масло имеет более крутую кривую зависимости толщины пленки EHL от температуры, чем смазки PAO и PAG.
При T <80 ° C минеральное масло дает более толстые пленки, чем смазка PAO, а при T <57 ° C минеральное масло дает более толстые пленки, чем смазка PAG. В диапазоне 70 ° C <90 ° C разница между толщиной пленки EHL минеральных смазочных материалов и смазок на основе полиальфаолефинов составляет всего 5 процентов. В этом же диапазоне температур смазка PAG дает более толстые пленки, которые на 16–37 процентов толще, чем у минерального масла.
Таблица 2. Толщина пленки EHL, нормированная на
Толщина пленки минерального масла при 80 ° C
В качестве примера значения толщины пленки рассмотрим ее влияние на срок службы подшипников качения. Если внутреннее кольцо подшипника работает при 70 ° C и смазывается минеральным маслом ISO 320, таблица 2 или рисунок 3 дает увеличение на 1,35868 / 1,00000 = 1,36 (36 процентов) по сравнению с минеральным маслом при 80 ° C. Синтетическое масло PAG имеет толщину пленки 1,57558 / 1,00000 = 1.58 (58 процентов) больше, чем у минерального масла при 80 ° C.
Преимущество использования смазки PAG перед минеральным маслом демонстрируется увеличением толщины пленки на 1,58 / 1,36 = 1,16 (16 процентов).
Для этого примера DIN ISO 281 показывает, что увеличение толщины пленки на 16 процентов увеличивает срок службы подшипника более чем в четыре раза (129 000 часов с PAG по сравнению с 31 500 часами с минеральным маслом).
Для зубчатой передачи, смазываемой маслом ISO 320 и работающей при температуре зуба 80 ° C, толщина пленки синтетического масла PAG на 27 процентов больше, чем у минерального масла.AGMA 925-A03 показывает, что вероятность износа с маслом PAG составляет менее 5 процентов, тогда как с минеральным маслом вероятность износа составляет 25 процентов.
Практическое руководство по выбору смазочного материала
(как показано на рисунке 3):
Масла PAG имеют значительно более толстую пленку, чем PAO и минеральные масла, во всем диапазоне практических температур.
Между ПАО и минеральными маслами существует небольшая разница в диапазоне температур от 70 ° C до 90 ° C.В этом же диапазоне температур смазка PAG дает на 16–37 процентов более толстую пленку, чем минеральное масло.
При температурах ниже 70 ° C минеральные масла и масла PAG имеют значительно большую толщину пленки, чем масла PAO.
Для температур выше 90 ° C масла PAO и PAG имеют значительно большую толщину пленки, чем минеральные масла.
Самый быстрый словарь в мире: словарь.com
коэффициент вязкости мера сопротивления потоку жидкости под действием приложенной силы
коэффициент упругости (физика) отношение приложенного напряжения к изменению формы упругого тела
коэффициент трения отношение веса объекта, перемещаемого по поверхности, к силе, которая поддерживает контакт между объектом и поверхностью
коэффициент отражения доля лучистой энергии, которая отражается от поверхности
добросовестный, отличается особой осторожностью и большими усилиями
коэффициент расширения: относительное изменение длины, площади или объема на единицу изменения температуры при заданном постоянном давлении
единица вязкости единица измерения вязкости
коэффициент корреляции статистика, показывающая, насколько близко две переменные взаимозависимы
коэффициент самоиндукции отношение электродвижущей силы, создаваемой в цепи за счет самоиндукции, к скорости изменения порождающего ее тока, выраженное в генри
коэффициент поглощения: мера скорости уменьшения интенсивности электромагнитного излучения (в виде света), когда оно проходит через данное вещество; доля падающей лучистой энергии, поглощенная на единицу массы или толщины поглотителя
коэффициент согласования Коэффициент согласования (согласования) между разными наборами ранжирования одного и того же набора вещей
абсолютная вязкость мера сопротивления потоку жидкости под действием приложенной силы
эффективно быть эффективным без потери времени, усилий и затрат
коэффициент взаимной индукции мера индукции между двумя цепями
научный факт наблюдение, которое неоднократно подтверждалось и принимается за истину (хотя его истинность никогда не бывает окончательной)
динамическая вязкость — мера сопротивления потоку жидкости под действием приложенной силы
постоянное число, служащее мерой некоторого свойства
эффективность способность или мощность для достижения желаемого результата
род Malvaviscus малый род кустарников Центральной и Южной Америки: мальвы восковые
Инверсионное исследование коэффициента вертикальной вихревой вязкости на основе модели внутреннего прилива с сопряженным методом
На основе модели внутреннего прилива в изопикнических координатах с помощью сопряженного метода инверсия пространственно изменяющегося коэффициента вертикальной вихревой вязкости (VEVC) изучается по двум направлениям. группы численных экспериментов.В первой группе обсуждается влияние схем независимых точек (IPS) на инверсию параметров. Результаты показывают, что VEVC можно успешно инвертировать с помощью IPS, а модель имеет лучшую производительность с оптимальными IPS. Используя оптимальные IPS, полученные в первой группе, инверсия VEVC на двух различных гауссовских топографиях дна выполняется во второй группе. Кроме того, также исследуются характеристики двух методов оптимизации, один из которых является методом Бройдена-Флетчера-Гольдфарба-Шанно с ограниченной памятью (L-BFGS), а другой — методом упрощенного градиентного спуска (GDM-S).Результаты экспериментов показывают, что эта сопряженная модель способна инвертировать VEVC с пространственным распределением, независимо от того, какой метод оптимизации выбран. Метод L-BFGS имеет лучшие характеристики с точки зрения скорости сходимости и результатов инверсии. В общем, метод L-BFGS является более эффективным и действенным методом оптимизации, чем GDM-S.
1. Введение
Внутренний прилив, который представляет собой внутреннюю волну приливной частоты, является повсеместным явлением в океанах.Рэттрей [1], Бейнс [2], Белл [3], Бейнс [4], Крейг [5], Геркема [6] и Ллевеллин Смит и Янг [7] разработали теоретические модели и получили некоторые аналитические решения внутреннего прилива. на идеальных топографиях. Эти теоретические модели помогли им исследовать возникновение и распространение внутренних приливов. Хотя в теории внутренних приливов был достигнут большой прогресс и были проведены некоторые аналитические работы, из-за сложности проблем можно предложить лишь небольшое количество решений.По этой причине количественный анализ, имеющий практическое значение, по-прежнему должен опираться на сочетание численного моделирования, теоретического анализа, эксперимента и наблюдения. Численное моделирование является эффективным методом морских исследований и широко используется при исследовании внутренних приливов и отливов. Канг и др. [8] исследовали внутренний прилив около Гавайев с помощью двумерной двухслойной численной модели и подтвердили, что внутренний прилив был вызван баротропным воздействием на Гавайском хребте и распространялся в северо-северо-восточном и юго-юго-западном направлениях.На основе высокоточной трехмерной модели Принстонского океана (POM) Нива и Хибия [9] получили распределение внутреннего прилива в Тихом океане с использованием спутниковых данных TOPEX / Poseidon (T / P). Cummins et al. [10] смоделировали генерацию и распространение внутренних приливов вблизи Алеутского хребта, используя данные T / P альтиметра. Сравнение данных альтиметра и результатов их моделирования показало хорошее согласие для фазы, что также свидетельствует о доле волн вблизи Алеутского хребта.С помощью трехмерного ПОМ Нива и Хибия [11] исследовали распределение и энергию внутреннего прилива вокруг края континентального шельфа в Восточно-Китайском море. Результаты их численных экспериментов показали, что внутренние приливы эффективно генерируются на таких рельефных участках, как морские хребты, цепи островов и проливы. Ян и др. [12] модифицировали POM для изучения генерации внутреннего прилива и его влияния на поверхностный прилив в Южно-Китайском море. Также оценивалась конверсия баротропной энергии в бароклинную энергию над топографическими гребнями в проливе Лусон.
Определение коэффициента вертикальной вихревой вязкости (VEVC), который описывает вертикальное перемешивание в океане, играет важную роль в изучении энергообмена и транспортировки материалов. VEVC обычно рассматривается как постоянная величина в численных моделях. Схемы для определения VEVC в основном включают модель гипотезы длины смешения Прандтля, модель смешения Пакановского-Филандера [13] и некоторые более сложные модели турбулентного замыкания. Было проведено множество исследований для изучения вариаций VEVC [14–18].Все эти упомянутые исследования показывают, что из-за различной интенсивности вертикального перемешивания в морской воде VEVC следует рассматривать не как константу, а как параметр с пространственным распределением.
Спутниковые технологии дистанционного зондирования и другие связанные с ними технологии предоставляют нам большое количество данных. Таким образом, одна из важнейших задач физической океанографии — эффективно и точно использовать данные, а также объединять данные наблюдений с существующими численными моделями.Действительно, усвоение данных сопряженным методом обеспечивает эффективный доступ к этим миссиям. Использование сопряженного метода в морской науке восходит к 1980-м годам. Сопряженная модель позволяет оптимизировать параметры управления при численном моделировании. Беннет и Макинтош [19] применили мысль о слабых ограничениях для решения приливной проблемы и проблемы геострофического потока. Ю и О’Брайен [20] ассимилировали метеологические и океанографические данные в модели океанического слоя Экмана и вывели неизвестное граничное условие, неизвестную вертикальную вихревую вязкость и текущее поле.Основываясь на приливной модели с методом двухуровневой чехарды, Ларднер [21] инвертировал открытые граничные условия в трех тестовых задачах. Зайлер [22] использовал сопряженный метод для ассимиляции наблюдений в квазигеострофической модели океана и оценил значения боковых границ в идеальных экспериментах. Навон [23] написал резюме оценки параметров в метеорологии и океанографии с точки зрения приложений с четырехмерными вариационными методами ассимиляции данных. Используя компилятор автоматического дифференцирования, Аюб [24] построил сопряженную модель общей циркуляции океана Массачусетского технологического института и инвертировал открытые граничные условия в Северной Атлантике.Чжан и Лу [25] разработали трехмерную нелинейную численную приливную модель с сопряженным методом и разработали несколько численных экспериментов для оценки трех видов параметров, включая открытые граничные условия, коэффициенты донного трения и коэффициенты вертикальной вихревой вязкости. Чжан и Лу [26] использовали двумерную приливную модель для изучения инверсии коэффициентов придонного трения в Бохайском и Желтом море с помощью сопряженного метода. Chen et al. [27] построили трехмерную внутреннюю приливную модель с помощью сопряженного метода и оценили шесть различных видов открытых граничных условий для четырнадцати типов топографии.Основываясь на приливной модели, Чжан и Чен [28] провели несколько полуидеализированных экспериментов для оценки частично и полностью пространственно изменяющихся открытых граничных условий. Cao et al. [29] исследовали инверсию открытых граничных условий с помощью трехмерной внутренней приливной модели и смоделировали внутренний прилив вокруг Гавайев путем ассимиляции данных T / P.
Настоящий документ преследует две основные цели. Один из них — изучить инверсию VEVC с помощью внутренней приливной модели и сопряженного метода.Согласно приведенным выше введениям, было проведено множество исследований для изучения инверсии управляющих параметров внутреннего прилива, таких как открытое граничное условие [29, 30] и условие придонного трения [31, 32]. Однако найдено мало работ по изучению инверсии VEVC. Поскольку VEVC является решающим фактором для описания вертикального перемешивания в океане, необходимо обратить внимание на инверсию VEVC. Другая цель — провести вычислительное исследование производительности метода градиентного спуска и метода Бройдена-Флетчера-Голдфарба-Шанно с ограниченной памятью (L-BFGS) для инверсии VEVC на основе модели, построенной Chen et al.[27]. Оба метода не требуют каких-либо оценок матриц Гессе, а не требуют векторов градиента и, таким образом, являются выполнимыми с вычислительной точки зрения. Chen et al. [30] провели сравнительное исследование нескольких методов оптимизации, но именно обращение открытых граничных условий является одномерным случаем. Осуществимость этих методов оптимизации для двумерного случая, такого как инверсия VEVC, требует дальнейших исследований.
Две группы численных экспериментов выполнены для изучения инверсии пространственно изменяющихся VEVC на основе модели внутренних приливов в изопикнических координатах с использованием сопряженного метода.В первой группе обсуждается влияние схем независимых точек (IPS) на инверсию параметров. Вторая группа исследует инверсию VEVC на двух различных гауссовских топографиях дна и характеристики двух методов оптимизации, которые являются методами GDM-S и L-BFGS.
Этот документ организован следующим образом. Раздел 2 кратко знакомит с сопряженной приливной моделью и методологией. Два метода оптимизации, включая методы GDM-S и L-BFGS, описаны в разделе 3.В разделе 4 подробно представлены план и процесс экспериментов. Результаты экспериментов обсуждаются в разделе 5. Наконец, мы подведем итоги и сделаем некоторые выводы в разделе 6.
2. Введение в численную модель
В данной статье используется внутренняя приливная модель с изопикническими координатами с методом сопряженной ассимиляции. Модель внутреннего прилива состоит из двух частей. Одна представляет собой прямую модель с определяющими уравнениями, а другая — сопряженную модель с сопряженными уравнениями.Эти две модели используются для имитации внутреннего прилива и оптимизации контрольных переменных соответственно. Chen et al. [27] представили две части очень подробно и проверили разумность и осуществимость модели. Формулировка не будет представлена в этой статье. В этой части подробно описываются вывод настройки VEVC, введение метода двух оптимизаций, проверка сопряженного метода и схема независимых точек (IPS).
2.1. Проверка сопряженного метода
Согласно уравнениям и выводам Chen et al.[27], можно вывести формулу инвертирования VEVC. Первая производная функции Лагранжа по отношению к VEVC получается следующим образом: где — значение VEVC на сетке в -м слое. Градиент функций стоимости по отношению к VEVC в сетке может быть выведен следующим образом: где — плотность потенциала в th слое, и — горизонтальные скорости на th временном шаге, и — сопряженные переменные и, соответственно, и — начальная толщина -го слоя. Подробный вывод (2) представлен в приложении.
Точное программирование сопряженного вычисления в таких задачах, как настоящая, довольно сложно, и опыт показал, что очень важно проверить точность сопряженного вычисления, прежде чем приступать к минимизационным прогонам [33]. В этом разделе проверяется корректность сопряженного метода. Возьмите член первого порядка в разложении Тейлора для функции стоимости, и мы получим следующее уравнение:
Здесь — общая точка управляющей переменной, — это вычисленный градиент и — произвольный единичный вектор в пространстве параметров.На основании (3) функцию можно записать следующим образом: где — небольшое вещественное число, не равное нулю. Если сопряженная методика верна, предполагается, что согласно (4). В этой статье переменная VEVC рассматривается как и проверка сопряженного метода основана на (4).
Для проверки точности сопряженного метода проводятся два эксперимента, в которых используются два разных типа. Различные направления вектора — это и соответственно.
На рисунке 1 показаны тенденции приближения к 0.Понятно, что в обоих экспериментах, когда значение меньше 10 −3 , значения (сплошные линии) оба очень близки к 1 (пунктирные линии). Уравнение доказано и проверена корректность градиента, вычисленного в сопряженной модели.
2.2. Схема независимых точек
Доступных данных наблюдений может быть недостаточно, а определяемые параметры управления могут быть чрезмерными на практике. Это может вызвать некорректность задачи инверсии. Ричардсон и Панчанг [34] впервые отметили, что при применении сопряженного метода при большой ошибке в данных решение будет нестабильным и не уникальным.Многие исследователи добились прогресса в решении этой проблемы. Была проделана большая работа [26, 27, 30, 32], чтобы доказать возможность и осуществимость схемы независимых точек (IPS) при решении некорректных задач инверсии.
В этой статье IPS используется для оптимизации параметра управления. Основная идея IPS заключается в следующем: некоторые сетки (например,) выбираются как независимые точки; предполагается, что он представляет значение VEVC в сетке, поэтому значения VEVC во всех сетках могут быть вычислены с помощью метода линейной интерполяции.Вычислительная формула имеет следующий вид: где — весовой коэффициент формы Крессмана [35]: где — межцентровое расстояние между и — радиус влияния. Согласно (5), градиент относительно может быть записан как где — градиент относительно VEVC на сетке и может быть вычислен с использованием формулы (2).
В соответствии с разделом 2.1 необходимо проверить правильность градиента по отношению к независимым точкам. Согласно (5) возмущения, применяемые к независимым точкам, оказывают линейное влияние на возмущения, применяемые к независимым точкам.Сходимости для независимых точек останутся прежними после линейного преобразования для независимых точек.
Значения VEVC в независимых сетках могут быть вычислены внутри модели, а значения в других сетках получены путем интерполяции с использованием (5). Тогда получается пространственное распределение VEVC по всей площади.
3. Алгоритмы оптимизации
Было много крупномасштабных методов оптимизации для решения задачи минимизации [36]. Четыре основных метода — это метод линейного поиска (например,g., Wolfe and Goldstein), метод доверительной области, метод сопряженных градиентов (например, Флетчера-Ривза) и метод квазиньютона (например, BFGS и L-BFGS). Однако количество исследований, в которых обсуждается эффективность различных методов оптимизации в метеорологических и океанографических приложениях, все еще относительно невелико [30]. Метод линейного поиска требует повторных вычислений функции стоимости и градиента. Поэтому он тратит слишком много вычислительных ресурсов во время численного моделирования, особенно для физической океанографии.Кроме того, в некоторых случаях методы линейного поиска могут давать сбой [37]. Метод L-BFGS обычно используется для решения крупномасштабных задач океанографии и метеорологии [30, 38, 39]. Chen et al. [30] провели вычислительное исследование характеристик метода L-BFGS и двух версий метода градиентного спуска с моделью внутреннего прилива. В их работе применяется упрощенный метод градиентного спуска, позволяющий избежать слишком большого количества вычислений. Длина шага выбирается исходя из опыта моделиста.По сравнению с другими методами, этот план имеет два основных преимущества. Один из них — это меньшее использование вычислительных ресурсов, а другой — более управляемый процесс оптимизации. Многие исследования доказали возможность использования этого метода [25–27, 31, 32].
Вообще говоря, численные методы для решения задач минимизации имеют аналогичную итерационную формулу, которая выглядит следующим образом: где и — априорные и скорректированные значения VEVC в -й итерации, соответственно, и и представляют длину шага итерации и направление поиска, соответственно.Существует множество методов определения направления поиска. В этой статье используются два различных метода оптимизации: GDM-S и L-BFGS.
3.1. Метод градиентного спуска (GDM)
GDM — это простой и выполнимый метод определения направления поиска следующим образом: где, и — зональный индекс, меридиональный индекс и индекс слоя расчетной сетки, соответственно; представляет шаг итерации. — норма градиента функции стоимости относительно VEVC на й итерации.
В GDM-S длина шага выбирается постоянной в соответствии с опытом разработчика модели. Мы исследовали характеристики различных значений и выбрали 0,006 как лучший выбор. Оптимизированное значение VEVC получается после того, как VEVC в каждой сетке настроен согласно (8) и (9).
3.2. Метод L-BFGS
L-BFGS — это алгоритм оптимизации из семейства квазиньютоновских методов, который аппроксимирует алгоритм BFGS с использованием ограниченного объема памяти компьютера.Этот метод впервые описан в работе Nocedal [40], где он называется методом SQN. Это популярный алгоритм оценки параметров в машинном обучении [41, 42]. Из-за возникающих в результате линейных требований к памяти метод L-BFGS особенно хорошо подходит для задач оптимизации с большим количеством переменных.
Требуется, чтобы направление поиска было где-то
Обратите внимание, что это упрощение для удобства. Здесь,,, и. Многие исследования показали, что, как правило, эффективность L-BFGS не улучшается [43].Таким образом, количество поправок m, использованных в обновлении L-BFGS этой статьи, принято равным 5 [44]. Версия L-BFGS, используемая в этой статье, описана Лю и Нокедалом [44], а коды Фортрана одобрены Нокедалом [45].
4. Планирование экспериментов
Все эксперименты в этой статье проводятся в идеальной региональной зоне от 116 ° E до 124,17 ° E и от 18 ° до 23,17 ° N с учетом практического морского района, расположенного вокруг Лусона. пролив. Разрешающая способность по горизонтали есть и целиком сетки в области.Максимальная глубина установлена в 1000 метров. Коэффициент горизонтального вихря выбран равным, а коэффициент донного трения — равным. За местное значение принимается коэффициент Кориолиса. Учитывается только прилив и его угловая частота. Полный временной шаг составляет 496,86 с, что составляет 1/90 периода прилива. Все четыре границы являются открытыми границами, и граничные условия устанавливаются как локальные уровни воды в форме Flather.
Восточная и западная границы: положительная на восточной границе и отрицательная на западной границе.
Северная и южная границы: положительные на северной границе и отрицательные на южной.
— высота поверхности над ненарушенным уровнем моря. и — зональная скорость течения и меридиональная скорость течения соответственно. , и — возвышение поверхности, зональная и меридиональная скорость течения, относящиеся к граничной баротропной приливной силе, соответственно. — коэффициент Кориолиса и — частота приливов и отливов. — местная глубина воды и — ускорение свободного падения.
Аналогично Chen et al. [27], приливная сила на th временном шаге зависит от коэффициентов Фурье на четырех открытых границах, которые установлены равными 0 и установлены равными 1 (-1) на северной и западной (южной и восточной) границах.
Данные высотомера T / P широко распространены по всему океану, и их можно использовать для инвертирования VEVC. В этой работе мы выбрали 89 расчетных точек на основе особенностей распределения наблюдений T / P высотомера в качестве точек наблюдения (Рисунок 2).
В этой статье тестируются два вида топографии, и они генерируются на основе двух формул в (15), соответственно (рисунок 3).Морская вода в вычислительной зоне разделена на два слоя. Толщина каждого слоя соответственно составляет и. Потенциальные плотности соответствующего слоя равны и соответственно. Учтите, где высота рельефа, а MaxDepth — глубина воды.
Для каждого эксперимента оптимизацию VEVC можно реализовать с помощью следующих шагов.
Шаг 1. Дается предписанный VEVC и запускается прямая модель. Все время моделирования составляет 20 периодов прилива для получения стабильного результата моделирования.Подъемы воды на наблюдательных позициях рассматриваются как «псевдонаблюдения».
Шаг 2. Дается начальное значение управляющего параметра (VEVC) и запускается прямая модель для получения результатов моделирования всех переменных состояния, таких как скорость течения и высота воды. Рассчитывается значение функции стоимости.
Шаг 3. Разница между смоделированной высотой и «псевдонаблюдением» играет роль внешней силы сопряженной модели.Путем обратного интегрирования сопряженных уравнений по периоду приливов получаются значения сопряженных переменных.
Шаг 4. Используя формулу (2), наряду с переменными состояния и сопряженными переменными, полученными на шагах 2 и 3, вычисляется градиент функции стоимости относительно VEVC.
Шаг 5. Обновите неизвестные управляющие переменные с помощью определенного метода оптимизации.
Шаг 6. Если критерий остановки итерации достигнут, завершите итерацию и верните оптимизированный параметр.В противном случае обновите все параметры и вернитесь к шагу 2.
В экспериментах, описанных в этой статье, все начальные значения VEVC установлены на 0,005, а общее количество итераций может быть не более 100. Выбранный критерий сходимости заключается в том, что два последних значения функции стоимости достаточно близки, что определяется где и является последним и вторым последними значениями функции стоимости, соответственно.
Проведены две группы численных экспериментов: влияние IPS на инверсию VEVC изучается в первой группе; во второй группе исследуется способность этой модели внутренних приливов инвертировать различные виды VEVC с пространственным распределением.Два вида пространственного распределения VEVC заданы и представлены на рисунке 4. Для обоих распределений значение VEVC находится в диапазоне от m 2 / с до m 2 / с.
В первой группе проводится девять экспериментов, чтобы обсудить влияние IPS на инверсию VEVC. Расстояние между независимыми точками (IP) колеблется от 20 футов (длина 2 решеток) до 100 футов (длина 10 решеток), подробности приведены в таблице 1. Применяется топография A, а распределение (a) выбирается в соответствии с предписанным пространственное распределение ВЭВЦ.
| |||||||||||||||||||||||||||||||||||||||||||||||
В группе 2 проводится четыре численных эксперимента (NE), которые пронумерованы как NE1 ~ .Каждый эксперимент проводится методами GDM-S и L-BFGS. Информация о топографиях и предписанных VEVC для всех сетевых элементов приведена в таблице 2. IPS — это оптимальные схемы, полученные в первой группе. Остальные параметры точно такие же, как у Group One.
| ||||||||||||||||||
Все эксперименты в группе 1 и группе 2 выполняются в разделах с 6 по 6, описанные в этапах с 1 по 6. 4.Версия метода L-BFGS, используемая в этой статье, взята из работы Лю и Нокедала [44].
5. Результаты экспериментов и обсуждение
5.1. Результаты и обсуждения в первой группе
На рисунке 5 показаны отношения между средними абсолютными ошибками (MAE, которая отражает ошибку между результатом инверсии и заданным VEVC) и расстоянием между независимыми точками в первой группе.
Как показано на рисунке 5, MAE с различными методами оптимизации меняются по мере изменения IPS.Минимальные значения MAE для двух методов не совпадают (пунктирные линии). Минимальная MAE для GDM-S составляет 2 / с, а для метода L-BFGS — 2 / с. Соответствующие расстояния IP составляют 90 футов (длина 9 решеток, GDM-S) и 30 футов (длина 3 решеток, L-BFGS) соответственно. Согласно MAE, показанным на рисунке 5, оптимальные IPS для этих двух методов выбраны как IPS8 (GDM-S) и IPS 2 (L-BFGS).
5.2. Результаты и обсуждения второй группы
С соответствующими оптимальными IPS и итерационным процессом в разделе 4, VEVC инвертируются с помощью метода GDM-S (I) и метода L-BFGS (II), соответственно, и показаны результаты инверсии на рисунке 6.
Сравнение результатов инверсии с предписанными VEVC показывает, что все заданные пространственные распределения VEVC успешно инвертируются после 100 шагов итерации. Основные особенности всех дистрибутивов могут быть восстановлены очень хорошо. Поверхности перевернутого VEVC с L-BFGS намного более гладкие, чем у GDM-S. По сравнению с результатами инверсии с помощью GDM-S (левые панели) шаблоны с методом L-BFGS (правые панели) ближе к предписанному VEVC. Дополнительные статистические данные будут представлены в следующих параграфах.
MAE четырех численных экспериментов после ассимиляции вычислены и перечислены в таблице 3. Начальные значения MAE для всех NE составляют m 2 / с. Исходя из результатов, представленных в таблице 3, все MAE после ассимиляции более чем на один порядок величины ниже исходных значений, что означает успех для обоих из двух методов оптимизации. Обратите внимание, что MAE с методом L-BFGS довольно близки (менее m 2 / с и не могут быть различимы в таблице) и меньше половины от таковых с GDM-S.Этот результат демонстрирует способность метода L-BFGS определять общие ошибки.
| |||||||||||||||||||||||||||
, чтобы сравнить эффективность двух методов, чтобы сравнить эффективность двух методов. процентные доли сетей, в которых MAE меньше m 2 / с, что указано в таблице 4.С помощью GDM-S ошибки инверсии выводятся на один порядок величины примерно на 40% от всех сеток. Напротив, отношения всех NE с методом L-BFGS составляют 79,76%, без различий между NE. Это явление указывает на то, что метод L-BFGS эффективен в большем количестве вычислительных сетей, чем GDM-S. Кроме того, метод L-BFGS сохраняет свою эффективность независимо от того, какая топография применяется.
Комбинируя шаблоны инверсии, ошибки инверсии VEVC и анализ эффективности, можно сделать выводы, что L-BFGS имеет лучшую производительность в снижении ошибок инверсии. Наконец, мы подошли к истории оптимизации для всех экспериментов, проведенных во второй группе.Вариации функции стоимости, нормированной ее начальным значением, нормы градиента функции стоимости по отношению к VEVC и ошибки инверсии, показаны на рисунках 7 (a), 7 (b) и 7 (c), соответственно, в зависимости от шага итерации. Обратите внимание, что все эксперименты с методом L-BFGS достигают критерия сходимости и останавливаются после 4 итераций, что указывает на то, что время вычисления для метода L-BFGS составляет одну двадцать пятую от времени вычисления для GDM-S.Рисунок 7 (a) показывает, что все функции затрат имеют тенденцию к снижению на протяжении итерационного процесса и уменьшаются более чем на 2 (7) порядков для GDM-S (метод L-BFGS), что означает, что окончательные различия между значение моделирования и наблюдения этих двух методов меньше одной десятой и одной тысячной от их начальных значений, соответственно. Как показано на рисунке 7 (b), нормы градиента функции затрат по отношению к VEVC снижаются более чем на 1 порядок (GDM-S) и 4 порядка (L-BFGS) по сравнению с их соответствующие начальные значения.Это указывает на то, что результат инверсии становится все ближе к заданному VEVC во время итерации. Как показано на Рисунке 7 (c), ошибки инверсии для двух методов продолжают уменьшаться на протяжении итераций, пока не будут выполнены критерии остановки. В общем, функции стоимости, нормы градиента и ошибки инверсии VEVC имеют устойчивый спад, что демонстрирует, что эта сопряженная модель способна инвертировать VEVC. Более того, методы GDM-S и L-BFGS эффективны с точки зрения инверсии управляющих параметров с пространственным распределением внутреннего прилива. На рисунке 7 также ясно видно, что скорость сходимости для функций стоимости, норм градиента и ошибок инверсии VEVC намного быстрее с методом L-BFGS, чем с GDM-S, что согласуется с классические теории о скорости сходимости квазиньютоновского метода и GDM [36]. Эта тенденция также согласуется с результатами численных экспериментов по обращению открытых граничных условий в Chen et al. [30]. Без сомнения, метод L-BFGS является более эффективным и действенным методом оптимизации для инвертирования пространственно изменяющегося VEVC.Однако GDM-S легче понять и реализовать в модели. Более того, длина шага и направление поиска в процессе GDM-S могут свободно контролироваться разработчиками моделей, что очень удобно на практике. Следовательно, для инверсии VEVC GDM-S также следует рассматривать как выбор. 6. Резюме и выводыОснованная на внутренней приливной модели с изопикническими координатами, в данной статье исследуется инверсия VEVC. Серия численных экспериментов проводится для изучения факторов влияния на инверсию VEVC в четырех аспектах: схемы независимых точек (IPS), топография, пространственное распределение VEVC и методы оптимизации.Для каждого эксперимента функция стоимости, норма градиента функции стоимости относительно VEVC и ошибка инверсии вычисляются и детально анализируются. IPS представлена и обсуждается в первой группе. Все VEVC можно успешно инвертировать с помощью IPS. MAE рассматривается как критерий сравнения результата. После сравнения 9 экспериментов подтверждается правильность IPS и выбираются оптимальные IPS для методов GDM-S и L-BFGS соответственно. На основе оптимальных IPS в первой группе, два типа распределений VEVC успешно инвертируются с помощью этой сопряженной модели на двух типах топографии во второй группе. MAE после оптимизации находятся на уровне 10 −4 (10 −5 ) для GDM-S (L-BFGS), что на один (два) порядка величины ниже начального значения. Все функции затрат и их нормы градиента по отношению к отведению VEV удовлетворительно снижаются, независимо от того, какой метод оптимизации выбран. По сравнению с GDM-S, метод L-BFGS имеет значительно лучшую производительность не только с точки зрения скорости сходимости, но и с точки зрения конечных результатов инверсии.Время вычисления для метода L-BFGS намного короче, чем для GDM-S. Подводя итог, можно сказать, что метод L-BFGS является более эффективным и действенным методом, чем GDM-S, с точки зрения инверсии VEVC. Тем не менее, GDM-S более удобен и управляем, поэтому его не следует игнорировать и следует серьезно отнестись к выбору инверсии VEVC с пространственным распределением. Успех численных экспериментов закладывает прочную основу для практических экспериментов и побуждает нас проводить эксперименты в практической морской зоне с измеренными данными и реальными данными высотомера T / P. ПриложениеВывод (2)Начнем с основных уравнений Чена и др. [27]. Слой 1 (поверхностный слой) Слой () Слой (нижний слой) Переменные и фон определяющих уравнений были подробно представлены в работе Чена [27]. Мы не будем повторять их в этой части. Границы раздела и трения выражаются где — коэффициент вертикальной вихревой вязкости, и. Функция стоимости определяется как точно такая же, как в [27].Тогда функция Лагранжа определяется, как в случаях, когда те же определения применяются в (A.2a) ~ (A.2c) и (A.3a) ~ (A.3c). Тогда функция Лагранжа может быть записана как где, и функции, и, соответственно, определены как Обратите внимание, что (A.11) ~ (A.13) не содержат переменную, что означает, что функция Лагранжа может быть записана как Наконец, в соответствии с типичной теорией метода множителей Лагранжа, у нас есть следующая производная первого порядка функции Лагранжа относительно управляющего параметра: тогда градиент функции стоимости относительно переменной может быть выведен из (A. | |||||||||||||||||||||||||||

