В чем измеряется динамическая вязкость – Вязкость — Википедия

Единицы измерения вязкости

Единицы измерения вязкости

Программа КИП и А

Вязкость — свойство газов и жидкостей оказывать сопротивление необратимому перемещению одной их части относительно другой при сдвиге, растяжении и других видах деформации.

Динамическая вязкость

Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.

  В международной системе единиц (СИ), динамическая вязкость измеряется в Паскаль — секундах [Па·с].

Существуют также внесистемные величины измерения динамической вязкости. Наиболее распространенная в системе СГС — пуаз [П] и ее производная сантипуаз [сП].

Также динамическая вязкость может измеряться в [дин·с/см²] и [кгс·с/м²] и производных от них единицах.

Соотношение между единицами динамической вязкости:

• 1 Пуаз [П] = 1 дин·с/см² = 0.010197162 кгс·с/м² = 0.0000010197162 кгс·с/см² = 0.1 Па·с = 0.1 Н·с/м²
• 1 Сантипуаз [сП] = 0.0001010197162 кгс·с/м² = 0.01 П = 0.001 Па·с
• 1 кгс·с/м² = 98.0665 П = 9806.65 сП = 9.80665 Па·с

США и Британия

В виду того, что в некоторых англоязычных странах сила и площадь поверхности может измеряться в отличных от системы СИ единицах, могут применяться отличные единицы измерения динамической вязкости.

• 1 Фунт сила секунда на дюйм² [lbf·s/in²] = 6894.75729316836 Па·с = 144 lbf·s/ft²
• 1 Фунт сила секунда на фут² [lbf·s/ft²] = 47.88025898034 Па·с

Кинематическая вязкость

Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ и определяется формулой:
  ν = µ / ρ, где µ — динамическая вязкость, Па·с, ρ — плотность жидкости, кг/м³.

В международной системе единиц (СИ), кинематическая вязкость измеряется в квадратных метрах на секунду [м²/с].

  Также широко используется внесистемная единица — cтокс [Ст] и ее производная — сантистокс [сСт].

Соотношение между единицами кинематической вязкости:

• 1 Ст = 0.0001 м²/с = 1 см²/с
• 1 сСт = 1 мм²/с = 0.000001 м²/с
• 1 м²/с = 10000 Ст = 1000000 сСт

США и Британия

В виду того, что в некоторых англоязычных странах сила и площадь поверхности может измеряться в отличных от системы СИ единицах, могут применяться отличные единицы измерения кинематической вязкости.

• 1 м²/с = 1550.0031000062 квадратных дюймов в секунду [in²/s]
• 1 м²/с = 10.76391041670972 квадратных футов в секунду [ft²/s]

 

www.axwap.com

Вязкость жидкости

Содержание

Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.

Физический смысл вязкости

Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример. Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ₁

Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ₁.

Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.

Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде

где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения

μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.

Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.

Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу

Вязкость кинематическая, динамическая и абсолютная

Теперь определимся с различными понятиям вязкости:

Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па*с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.

Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.

Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.

Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести

Абсолютная вязкость получается при умножении кинематической вязкости на плотность. В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.

Коэффициент вязкости жидкости

В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости

ν = μ / ρ,

где ρ – плотность жидкости.

Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.

В физической системе единиц кинематическая вязкость имеет единицу измерения см²/с и называется Стоксом(Ст).

Вязкость некоторых жидкостей

Жидкость	t, °С	ν, Ст
Вода	0	0,0178
Вода	20	0,0101
Вода	100	0,0028
Бензин	18	0,0065
Спирт винный	18	0,0133
Керосин	18	0,0250
Глицерин	20	8,7
Ртуть	0	0,00125

Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью

ξ = 1/μ

Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры. Для различных жидкостей зависимость вязкости от температуры получается различной.

Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.

Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.

Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.

Методы измерения вязкости. Метод Стокса.

Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.

Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.

Существует следующие методы определения вязкости жидкости.

Капиллярный метод.

Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.

Метод по Гессе.

Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.

Ротационный метод.

Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого. В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.

Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.

Метод Стокса

Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.

Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.

Видео по теме вязкости

Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.

www.nektonnasos.ru

Понятие динамической и кинетической вязкости

« Назад

Вязкостью называется свойство жидкости сопротивляться внешнему воздействию благодаря внутреннему трению, возникающему между слоями.

Для определения вязкости существует два основных параметра: динамическая вязкость и кинематическая вязкость, которые связаны между собой соотношением:

Где ν – кинематическая вязкость, м²/с;

µ — динамическая вязкость, Па*с;

ρ – плотность жидкости, кг/м³.

Между слоями жидкости, движущимися друг относительно друга, возникает сила. Эта сила прямо пропорциональна скорости движения и площади соприкосновения.

В 1687 году И. Ньютоном был установлен закон вязкого течения жидкости:

где τ – касательные напряжения;

Коэффициент пропорциональности µ и назвали динамической вязкостью жидкости.

Динамическая и кинематическая вязкости зависят от температуры рабочей среды. Причем для газов и жидкостей эта зависимость различна. Это связано с различием во взаимодействии молекул. Для капельных жидкостей оба коэффициента убывают с возрастанием температуры.

Для определения вязкости используются специальные приборы – вискозиметры (U-образная стеклянная трубка). Одно из колен вискозиметра содержит впаянный капилляр, который оканчивается шариком. Под шариком и над ним нанесены метки, которые ограничивают определенный объем.

Для определения вязкости жидкости необходимо выбрать эталонную жидкость, вязкость которой является известной величиной. Для определения вязкости рабочей жидкости используется формула:

где µ — вязкость рабочей жидкости;

µ₀ – вязкость эталонной жидкости;

t – время истечения через капилляр исследуемой жидкости;

t₀ – время истечения через капилляр эталонной жидкости;

ρ – плотность исследуемой жидкости;

ρ₀ – плотность эталонной жидкости.

Так же существует понятие условной вязкости. Это отношение времени истечения через вискозиметр испытуемой жидкости при рабочей температуре к времени истечения дистиллированной воды при температуре 20°С (водное число). Водное соотношение является постоянной величиной для каждого прибора. Это соотношения выражается условными градусами.

где ВУ – условная вязкость;

t_H2O – водное число.

Еще один метод определения вязкости жидкости – метод Стокса.

Он заключается в бросании различных шариков в жидкость и измерении скорости их падения. На шарик действуют три силы: сила тяжести, выталкивающая сила и сила сопротивления окружающей среды.

где F_тяж – сила тяжести;

m – масса шарика;

r – радиус шарика;

ρ_ш – плотность шарика.

где F_{A– выталкивающая сила.}

где F_{c– сила сопротивления окружающей среды;}

ϑ – скорость движения шарика.

Подставив выражения для сил, действующих на шарик в итоговое уравнение, можно найти вязкость жидкости:

где d – диаметр шарика;

t – время падения шарика;

l – расстояние, пройденной шариком.

 

 

 

« Назад

megatechnika.com

Стокс (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Стокс.

Стокс (русское обозначение: Ст; международное: St) — единица кинематической вязкости, входящая в систему единиц СГС. Названа в честь Дж. Г. Стокса. В Российской Федерации стокс допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность»^[1]. Международная организация законодательной метрологии (МОЗМ) относит стокс к единицам измерения, «которые могут временно применяться до даты, установленной национальными предписаниями, но которые не должны вводиться, если они не используются»^[2].

Один стокс равен кинематической вязкости, при которой динамическая вязкость среды плотностью 1 г/см³ равна 1 пз. Кинематическая вязкость равна отношению динамической вязкости к плотности среды и дает понятие о вязкости среды в определенных условиях — под действием силы тяжести. Это связано с методом измерения вязкости в капиллярном вискозиметре, когда измеряется время вытекания жидкости из калиброванной ёмкости через отверстие под действием силы тяжести.

В Международной системе единиц (СИ) единицей измерения вязкости служит м²/с: 1 Ст = см²/с = 10⁻⁴м²/с. На практике часто применяется в 100 раз меньшая единица — сантистокс (сСт, cSt): 1 сСт = 1 мм²/с = 10⁻⁶м²/с

Примерные вязкости некоторых веществ[править | править код]

Вещество		Вязкость, сСт
Вода		1,011
Мазут топочный М-100	при 80 °C	118
	при 100 °C	50
Дизельное топливо при 20 °C		3—6
Печное топливо при 20 °C		< 8
Судовое топливо IFO-380	при 50 °C	380
	при 100 °C	35

ru.wikipedia.org

Динамическая вязкость — это… Что такое Динамическая вязкость?

Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.

Прибор для измерения вязкости называется вискозиметром.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.

Вторая вязкость

Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Вязкость жидкостей

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = Ce^{w / kT}

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества V_M. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

Вязкость аморфных материалов

Вязкость аморфных материалов (например, стекла или расплавов), это термически активизируемый процесс^[1]:

где Q — энергия активации вязкости (кДж/моль), T — температура (К), R — универсальная газовая постоянная (8,31 Дж/моль•К) и A — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины Q_H при низких температурах (в стеклообразном состоянии) на малую величину Q_L при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют R_D < 2, в то время как ломкие материалы имеют .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

с постоянными A₁, A₂, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования T_g это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Вязкость

Если температура существенно ниже температуры стеклования T < T_g, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

с высокой энергией активации Q_H = H_d + H_m, где H_d — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а H_m — энтальпия их движения. Это связано с тем, что при T < T_g аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При T > > T_g двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

но с низкой энергией активации Q_L = H_m. Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Сила вязкого трения

Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.

Примечания

1. ↑ Я. И. Френкель. Кинетическая теория жидкостей. Ленинград, Наука, 1975.

См. также

Ссылки

• Аринштейн А., Сравнительный вискозиметр Жуковского Квант, № 9, 1983.
• Измерение вязкости нефтепродуктов — обзор методов и единиц измерения вязкости.
• R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
• M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
• M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
• Булкин П. С. Попова И. И.,Общий физический практикум. Молекулярная физика
• Статья в энциклопедии Химик.ру

Литература

• Я. И. Френкель. Кинетическая теория жидкостей. — Л.: «Наука», 1975.

Wikimedia Foundation. 2010.

dic.academic.ru

Вязкость — это… Что такое Вязкость?

Эта статья нуждается в дополнительных источниках для улучшения проверяемости. Вы можете помочь улучшить эту статью, добавив ссылки на авторитетные источники. Не подтверждённая источниками информация может быть поставлена под сомнение и удалена.

Характер падения тела в жидкости с малой (сверху) и с большой (снизу) вязкостью

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: Па·с = 10 пуаз) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹−10¹² Па·с

Прибор для измерения вязкости называется вискозиметром.

Сила вязкого трения

Сила вязкого трения F пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h:

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости.

Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.

Вторая вязкость

Вторая вязкость, или объёмная вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн, и экспериментально определяется путём измерения этого затухания.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где  — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность прямо пропорциональна давлению, а  — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как

Влияние температуры на вязкость газов

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:^[1]

где:

• μ = динамическая вязкость в (Па·с) при заданной температуре T,
• μ₀ = контрольная вязкость в (Па·с) при некоторой контрольной температуре T₀,
• T = заданная температура в Кельвинах,
• T₀ = контрольная температура в Кельвинах,
• C = постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже

См. также [1] (англ.).

Вязкость жидкостей

Динамический коэффициент вязкости

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение

где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Кинематическая вязкость

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной

и эта величина получила название кинематической вязкости. Здесь  — плотность жидкости;  — динамическая вязкость (см. выше).

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом:

1 сСт = 1мм²1c = 10⁻⁶ м²c

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье):

где  — тензор вязких напряжений.

Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.

Вязкость аморфных материалов

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс^[4]:

где  — энергия активации вязкости (кДж/моль),  — температура (К),  — универсальная газовая постоянная (8,31 Дж/моль·К) и  — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости изменяется от большой величины при низких температурах (в стеклообразном состоянии) на малую величину при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют , в то время как ломкие материалы имеют .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

с постоянными , , , и , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Вязкость

Если температура существенно ниже температуры стеклования , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

с высокой энергией активации , где  — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а  — энтальпия их движения. Это связано с тем, что при аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

но с низкой энергией активации . Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Относительная вязкость

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

где μ — динамическая вязкость раствора; μ₀ — динамическая вязкость растворителя.

Вязкость некоторых веществ

Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.

Вязкость воздуха

Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K

Вязкость воздуха зависит, в основном, от температуры. При 15.0 °C вязкость воздуха составляет 1.78·10⁻⁵ кг/(м·с), 17.8 мкПа.с или 1.78·10⁻⁵ Па.с.. Можно найти вязкость воздуха как функцию температуры с помощью Программы расчёта вязкостей газов

Вязкость воды

Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)

Динамическая вязкость воды составляет 8,90 × 10⁻⁴Па·с при температуре около 25 °C.
Как функция температуры T (K): (Па·с) = A × 10^B/(T−C)
где A=2.414 × 10⁻⁵ Па·с; B = 247.8 K ; и C = 140 K.

Значения вязкостей жидкой воды при разных температурах вплоть до точки кипения приведена ниже.

Температура [°C]	Вязкость [мПа·с]
10	1.308
20	1.002
30	0.7978
40	0.6531
50	0.5471
60	0.4668
70	0.4044
80	0.3550
90	0.3150
100	0.2822

Динамическая вязкость разных веществ

Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:

Примечания

См. также

Ссылки

• Аринштейн А., Сравнительный вискозиметр Жуковского Квант, № 9, 1983.
• Измерение вязкости нефтепродуктов — обзор методов и единиц измерения вязкости.
• R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
• M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
• M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
• Булкин П. С. Попова И. И.,Общий физический практикум. Молекулярная физика
• Статья в энциклопедии Химик.ру
• Седов Л. И. Механика сплошной среды, том 1

Литература

dal.academic.ru

Вязкость — Википедия

Поведение жидкости с малой (сверху) и с большой (снизу) вязкостью

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единица измерения в Международной системе единиц (СИ) — Па·с, в системе СГС — пуаз; 1 Па·с = 10 пуаз) и кинематическую вязкость (единица измерения в СИ — м²/с, в СГС — стокс, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром.

Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 10¹¹−10¹² Па·с.

Сила вязкого трения[править]

Сила вязкого трения F, действующая на жидкость, пропорциональна (в простейшем случае сдвигового течения вдоль плоской стенки^[1]) скорости относительного движения v тел и площади S и обратно пропорциональна расстоянию между плоскостями h:

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости. Этот закон был предложен Исааком Ньютоном в 1687 году и носит его имя (закон вязкости Ньютона). Экспериментальное подтверждение закона было получено в начале XIX века в опытах Кулона с крутильными весами и в экспериментах Хагена и Пуазёйля с течением воды в капиллярах^[2].

Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.

Вторая вязкость[править]

Вторая вязкость, или объёмная вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и (или) при учёте неоднородности коэффициента второй вязкости по пространству.

Если динамическая (и кинематическая) вязкость характеризует деформацию чистого сдвига, то вторая вязкость характеризует деформацию объёмного сжатия.

Объёмная вязкость играет большую роль в затухании звука и ударных волн, и экспериментально определяется путём измерения этого затухания.

Вязкость газов[править]

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

,

где  — средняя скорость теплового движения молекул, − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность прямо пропорциональна давлению, а  — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа , растущей с температурой как

Влияние температуры на вязкость газов[править]

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:^[3]

где:

• μ = динамическая вязкость в (Па·с) при заданной температуре T,
• μ₀ = контрольная вязкость в (Па·с) при некоторой контрольной температуре T₀,
• T = заданная температура в Кельвинах,
• T₀ = контрольная температура в Кельвинах,
• C = постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже

Газ	C [K]	T0 [K]	μ0 [мкПа с]
Воздух	120	291,15	18,27
Азот	111	300,55	17,81
Кислород	127	292,25	20,18
Углекислый газ	240	293,15	14,8
Угарный газ	118	288,15	17,2
Водород	72	293,85	8,76
Аммиак	370	293,15	9,82
Оксид серы(IV)	416	293,65	12,54
Гелий	79,4[4]	273	19[5]

См. также [1] (англ.).

Вязкость жидкостей[править]

Динамическая вязкость[править]

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:

Коэффициент вязкости (коэффициент динамической вязкости, динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение:

где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.

Кинематическая вязкость[править]

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной:

и эта величина получила название кинематической вязкости. Здесь  — плотность жидкости;  — коэффициент динамической вязкости (см. выше).

Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом:

1 сСт = 1 мм²1 c = 10⁻⁶ м²c

Условная вязкость[править]

Условная вязкость — величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма раствора через вертикальную трубку (определённого диаметра). Измеряют в градусах Энглера (по имени немецкого химика К. О. Энглера), обозначают — °ВУ. Определяется отношением времени истечения 200 см³ испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 см³ дистиллированной воды из того же прибора при 20 °С. Условную вязкость до 16 °ВУ переводят в кинематическую по таблице ГОСТ, а условную вязкость, превышающую 16 °ВУ, по формуле:

где  — кинематическая вязкость (в м²/с), а  — условная вязкость (в °ВУ) при температуре t.

Ньютоновские и неньютоновские жидкости[править]

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье — Стокса^[6]):

где  — тензор вязких напряжений.

Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.

Вязкость аморфных материалов[править]

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс^[7]:

где  — энергия активации вязкости (Дж/моль),  — температура (К),  — универсальная газовая постоянная (8,31 Дж/моль·К) и  — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости изменяется от большой величины при низких температурах (в стеклообразном состоянии) на малую величину при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда , или ломкие, когда . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса : сильные материалы имеют , в то время как ломкие материалы имеют .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением^[8]:

с постоянными , , , и , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Если температура существенно ниже температуры стеклования , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

с высокой энергией активации , где  — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а  — энтальпия их движения. Это связано с тем, что при аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

но с низкой энергией активации . Это связано с тем, что при аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Относительная вязкость[править]

В технических науках часто пользуются понятием относительной вязкости, под которой понимают отношение коэффициента динамической вязкости (см. выше) раствора к коэффициенту динамической вязкости чистого растворителя:

где μ — динамическая вязкость раствора; μ₀ — динамическая вязкость растворителя.

Вязкость некоторых веществ[править]

Для авиастроения и судостроения наиболее важно знать вязкости воздуха и воды.

Вязкость воздуха[править]

Зависимость вязкости сухого воздуха от давления при температурах 300, 400 и 500 K

Вязкость воздуха зависит в основном от температуры. При 15,0 °C вязкость воздуха составляет 1,78·10⁻⁵ кг/(м·с), 17,8 мкПа·с или 1.78·10⁻⁵ Па·с. Можно найти вязкость воздуха как функцию температуры с помощью Программы расчёта вязкостей газов

Вязкость воды[править]

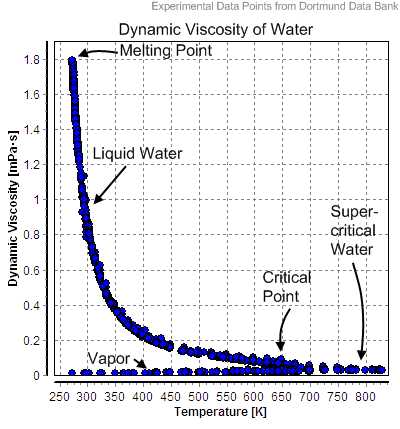Зависимость динамической вязкости воды от температуры в жидком состоянии (Liquid Water) и в виде пара (Vapor)

Динамическая вязкость воды составляет 8,90 × 10⁻⁴Па·с при температуре около 25 °C.
Как функция температуры T (K): (Па·с) = A × 10^B/(T−C)
где A=2,414 × 10⁻⁵ Па·с; B = 247,8 K ; и C = 140 K.

Значения вязкостей жидкой воды при разных температурах вплоть до точки кипения приведена ниже.

Температура [°C]	Вязкость [мПа·с]
10	1,308
20	1,002
30	0,7978
40	0,6531
50	0,5471
60	0,4668
70	0,4044
80	0,3550
90	0,3150
100	0,2822

Динамическая вязкость разных веществ[править]

Ниже приведены значения коэффициента динамической вязкости некоторых ньютоновских жидкостей:

Вязкость отдельных видов газов при давлении 100 кПа, [мкПа·с]

Газ	при 0 °C (273 K)	при 27 °C (300 K)
воздух	17,4	18,6
водород	8,4	9,0
гелий		20,0
аргон		22,9
ксенон	21,2	23,2
углекислый газ		15,0
метан		11,2
этан		9,5

Вязкость жидкостей при 25 °C

Жидкость:	Вязкость [Па·с]	Вязкость [мПа·с]
ацетон	3,06·10−4	0,306
бензол	6,04·10−4	0,604
кровь (при 37 °C)	(3—4)·10−3	3—4
касторовое масло	0,985	985
кукурузный сироп	1,3806	1380,6
этиловый спирт	1.074·10−3	1.074
этиленгликоль	1,61·10−2	16,1
глицерин (при 20 °C)	1,49	1490
мазут	2,022	2022
ртуть	1,526·10−3	1,526
метиловый спирт	5,44·10−4	0,544
моторное масло SAE 10 (при 20 °C)	0,065	65
моторное масло SAE 40 (при 20 °C)	0,319	319
нитробензол	1,863·10−3	1,863
жидкий азот (при 77K)	1,58·10−4	0,158
пропанол	1,945·10−3	1,945
оливковое масло	0,081	81
пек	2.3·108	2.3·1011
серная кислота	2,42·10−2	24,2
вода	8,94·10−4	0,894

1. ↑ В общем случае это не так.
2. ↑ О некоторых ошибках в курсах гидродинамики, с. 3-4.
3. ↑ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow, Birkhäuser, 2006, ISBN 0-387-26140-0 p. 46
4. ↑ data constants for sutherland’s formula
5. ↑ Viscosity of liquids and gases
6. ↑ Седов Л. И., Механика сплошной среды. М.: Наука, 1970. Т. 1, с. 166.
7. ↑ Френкель Я. И. Кинетическая теория жидкостей. —Ленинград, Наука, 1975. — стр. 226
8. ↑ Ojovan M. Viscous flow and the viscosity of melts and glasses. Physics and Chemistry of Glasses, 53 (4) 143—150 (2012).

• R.H. Doremus. J. Appl. Phys., 92, 7619-7629 (2002).
• M.I. Ojovan, W.E. Lee. J. Appl. Phys., 95, 3803-3810 (2004).
• M.I. Ojovan, K.P. Travis, R.J. Hand. J. Phys.: Condensed Matter, 19, 415107 (2007).
• Седов Л. И. Механика сплошной среды, том 1
• П. Н. Гедык, М. И. Калашникова. Смазка металлургического оборудования. М. Металлургия — 1976. — 380 с.

wp.wiki-wiki.ru