|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
способы определения ⋆ PumpUnion Москва —
При подборе промышленного насосного оборудования объемного принципа действия или при расчете систем трубопроводов, подборе клапанов и другого технологического оборудования на те или иные промышленные задачи мы часто сталкиваемся с проблемой определения вязкости жидкости. Что же нам делать в таком случае и как правильно измерить вязкость?
Существует несколько способов:
Для наиболее точного определения вязкости жидкости рекомендуется пользоваться специальными приборами, так называемыми вискозиметрами, которые бывают нескольких видов и отличаются не только по названию, но и по принципу действия. А это означает, что далеко не каждый вискозиметр универсален и подходит на все виды применений и сред. Причем хороший вискозиметр это зачастую не дешевое удовольствие и не каждая лаборатория может себе такое позволить. Поэтому на производстве часто случается так, что в нужный момент вискозиметра не оказывается под рукой. Что же нам делать в таком случае? Переходим к способу 2.
Поэтому на производстве часто случается так, что в нужный момент вискозиметра не оказывается под рукой. Что же нам делать в таком случае? Переходим к способу 2.
Можно использовать уже готовые таблицы данных вязкости или таблицы, позволяющие самостоятельно произвести в них расчет. Они обычно составляются для наиболее широко известных применений, таких как например сметана, шоколад, битум, полиол и других, измеренных при определенных внешних условиях сред. Это вполне очевидный и логичный способ. Однако, иногда случается так, что требуемой нам жидкости нет ни в одной из таких таблиц, или есть, но при других климатических условиях. Тогда нам остается вернуться к варианту с вискозиметром или же попробовать определить вязкость органолептическим способом оценки, иными словами на глаз.
В этом случае в помощь своим сотрудникам и коллегам мы хотим показать видео, на котором представлена линейка изменений вязкости жидкости, разделенная на наиболее популярные ступени.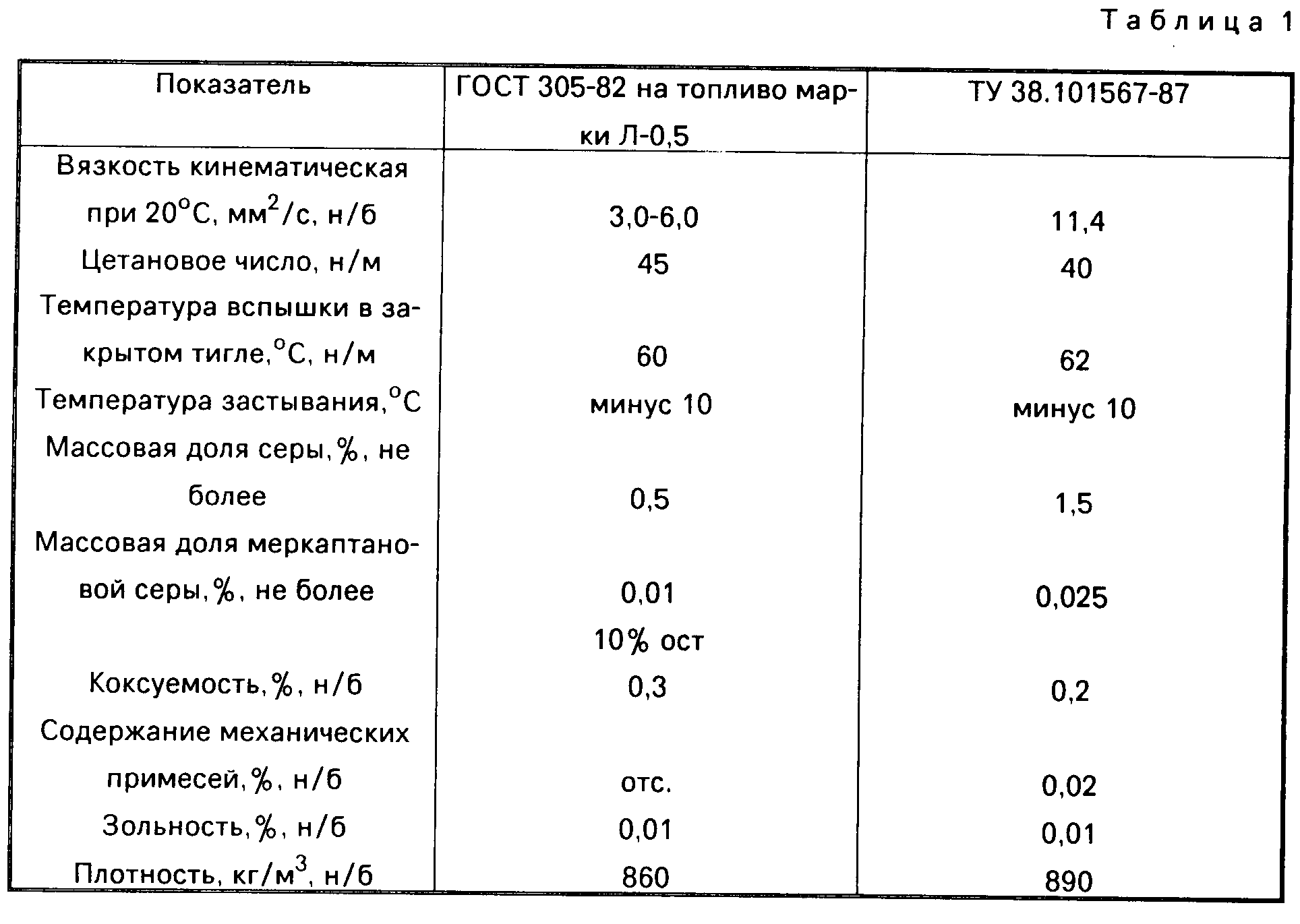 Этот способ может оказаться не настолько точен, как способ №1 и не подойдет в случае, если мы ни разу не видели исследуемую нами жидкость, как способ №2, но зато этот способ довольно удобен при работе с жидкостями, которые мы сами можем увидеть и потрогать, а потом сравнить увиденную вязкость с линейкой вязких сред, представленных на видео. Желаем удачи и спасибо за внимание!
Этот способ может оказаться не настолько точен, как способ №1 и не подойдет в случае, если мы ни разу не видели исследуемую нами жидкость, как способ №2, но зато этот способ довольно удобен при работе с жидкостями, которые мы сами можем увидеть и потрогать, а потом сравнить увиденную вязкость с линейкой вязких сред, представленных на видео. Желаем удачи и спасибо за внимание!
Эмалированное оборудование — Таблица вязкости жидкостей
Таблица вязкости распространенных жидкостей
Вязкость представляет собой способность любой жидкости течь. Вязкость жидкости является мерой ее устойчивости к сдвигающей силе. Это находит свое отражение в начальном и последующем этапах течения. Например, жидкости с высокой вязкостью требуется большая мощность для потока, чем жидкости с низкой вязкостью. Вязкость жидкости связана с температурой.
Стандартными единицами измерения вязкости являются пуаз (П), сантипуаз (сП), а также паскаль-секунда (Па·с). Преобразование между этими единицами:
1 П = 100 сП, 1 сП = 1 мПа·с, 1000 мПа·с = 1 Па·с
Вода имеет вязкость 1 сП и течет очень легко. Вязкость распространенных субстанций указана ниже:
Вязкость распространенных субстанций указана ниже:
Вода: 1 сП
Молоко: 3 сП
Растительное масло: 34 сП
Томатный соус: 176 сП
Глицерин: 880 сП
Меласса: 1760 сП
Клей: 3000 сП
Сироп: 8640 сП
Сметана: 15200 сП
| Жидкость | Абсолютная вязкость(сП) | Температура(℃) | Жидкость | Абсолютная вязкость(сП) | Температура(℃) |
| Вода | 1 | 20 | Грушевый сироп | 4000 | 70 |
| Воздух | 0.0178 | 20 | Концентрированный апельсиновый сок30 брикс | 630 | 21 |
| Алкоголь | 1.2 | 20 | Концентрированный апельсиновый сок30 брикс | 91 | 79 |
| Хлортетрациклин | 0. 9 9 |
20 | Концентрированный апельсиновый сок50 брикс | 2410 | 21 |
| Бензол | 0.6 | 20 | Соус для салата | 1300-2600 | 19 |
| Эфир | 0.2 | 20 | Кетчуп | 1000 | 29 |
| Йогурт | 152 | 40 | Томатная паста 30% | 195 | 19 |
| Яйцо | 150 | 4 | Дрожжевая суспензия | 20 | 19 |
| Молоко | 3 | 18 | Поваренное масло | 65 | 21 |
| Молочная сыворотка (48%сахара) | 180-1500 | 38 | Микстура от кашля | 190 | 29 |
| Сливки(жирность 30%) | 14 | 16 | Моющее средство | 1470 | 20 |
| Сливки(жирность 40%) | 48 | 16 | Крем для лица | 10000 | 21 |
| Сливки(жирность 50%) | 112 | 16 | Масло для волос | 5000 | 21 |
| Сливки(жирность 50%) | 55 | 32 | Эмульсия | 200 | 21 |
| Пиво | 1. 1 1 |
4.5 | Шампунь | 3000 | 35 |
| Шоколад | 17000 | 49 | Мыльный раствор | 82 | 60 |
| Шоколадное молоко | 280 | 49 | Клей | 3000 | 22 |
| Глюкоза | 4300-8600 | 75-85 | Глицерин | 1500 | 20 |
| Сок | 55-75 | 19 | Средний инвертный сироп | 2400 | 20 |
| Мед | 3000 | 20 | 180# тяжелое масло | 180 | 20 |
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings. ADD_COLLECTION_DESCRIPTION}}
ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article. content_lang.display}}
content_lang.display}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Коэффициент кинематической вязкости воды при температуре 25. Определение вязкости жидкости. Динамическая вязкость воды в зависимости от температуры
Вода H 2 O представляет собой ньютоновскую жидкость и ее течение описывается законом вязкого трения Ньютона, в уравнении которого коэффициент пропорциональности называется коэффициентом вязкости, или просто вязкостью.
Вязкость воды зависит от температуры. Кинематическая вязкость воды равна 1,006·10 -6 м 2 /с при температуре 20°С.
В таблице представлены значения кинематической вязкости воды в зависимости от температуры при атмосферном давлении (760 мм.рт.ст.). Значения вязкости даны в интервале температуры от 0 до 300°С. При температуре воды свыше 100°С, ее кинематическая вязкость указана в таблице на линии насыщения.
Кинематическая вязкость воды изменяет свою величину при нагревании и охлаждении. По данным таблицы видно, что с ростом температуры воды ее кинематическая вязкость уменьшается . Если сравнить вязкость воды при различных температурах, например при 0 и 300°С, то очевидно ее уменьшение примерно в 14 раз. То есть вода при нагревании становится менее вязкой, а высокая вязкость воды достигается если воду максимально охладить.
Значения коэффициента кинематической вязкости при различных температурах необходимы для вычисления величины числа Рейнольдса, которое соответствует определенному режиму течения жидкости или газа.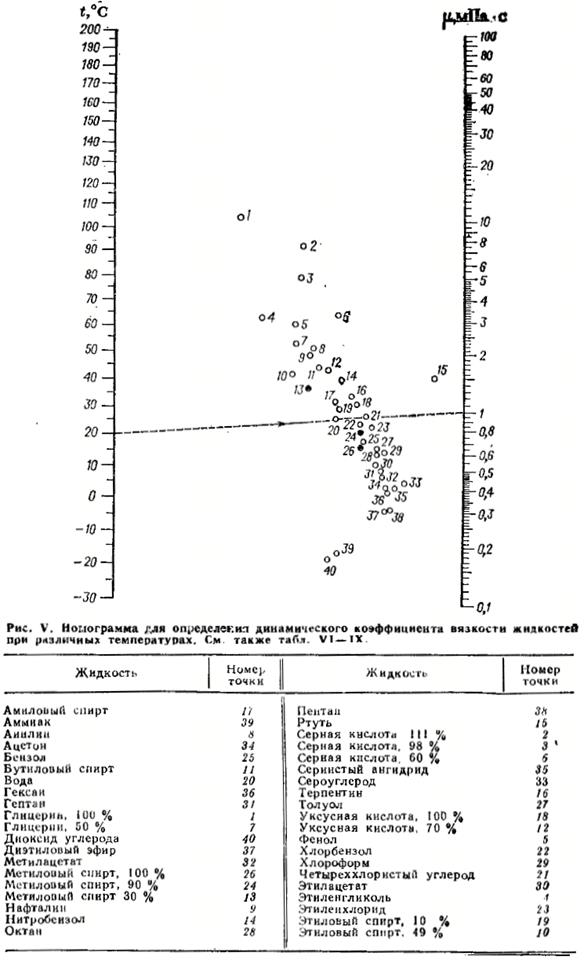
Если сравнить вязкость воды с вязкостью других ньютоновских жидкостей, например с , или с , то вода будет иметь меньшую вязкость. Менее вязкими, по сравнению с водой, являются органические жидкости – , бензол и сжиженные газы, например такие, как .
Динамическая вязкость воды в зависимости от температуры
Кинематическая и динамическая вязкость связаны между собой через значение плотности. Если кинематическую вязкость умножить на плотность, то получим величину коэффициента динамической вязкости (или просто динамическую вязкость).
Динамическая вязкость воды при температуре 20°С равна 1004·10 -6 Па·с. В таблице даны значения коэффициента динамической вязкости воды в зависимости от температуры при нормальном атмосферном давлении (760 мм.рт.ст.). Вязкость в таблице указана при температуре от 0 до 300°С.
Динамическая вязкость при нагревании воды уменьшается , вода становится менее вязкой и при достижении
Вода — это жидкость, без которой невозможна жизнь на земле. Но многие не знают, что она имеет много свойств, несколько видов и особенностей. Одна из них — вязкость, которая используется не только в физике, но и в других сферах знаний и жизни человека. Это такие отрасли, как медицина, косметология, кулинария, автомобильная промышленность. Еще один вид этой характеристики — условная вязкость — активно используется в нефтедобывающей промышленности, химии и физике.
Но многие не знают, что она имеет много свойств, несколько видов и особенностей. Одна из них — вязкость, которая используется не только в физике, но и в других сферах знаний и жизни человека. Это такие отрасли, как медицина, косметология, кулинария, автомобильная промышленность. Еще один вид этой характеристики — условная вязкость — активно используется в нефтедобывающей промышленности, химии и физике.
Что за явление — динамическая вязкость воды?
Растягиваясь, жидкое вещество претерпевает сопротивление. Аналогично происходит при сдвиге. Такое явление зависит от той скорости, которую развивают частицы жидкости при движении различных пластов воды. При воздействии пласта, передвигающегося быстрее, на пласт, движущийся более медленно, на первый план выступает ускоряющая сила. При обратном явлении действует тормозящая. Обе силы действуют в направлении к поверхностям пластов воды по касательной.
Отличительной особенностью является вязкость воды, сопротивляющаяся перемещению частиц в отношении друг друга. Она подразделяется на объемную и тангенциальную. Объёмная сопротивляется растяжению, она начинает действовать при распространении в воде различных звуковых волн. Тангенциальная вязкость способна оказывать сопротивление сдвигающему усилию.
Она подразделяется на объемную и тангенциальную. Объёмная сопротивляется растяжению, она начинает действовать при распространении в воде различных звуковых волн. Тангенциальная вязкость способна оказывать сопротивление сдвигающему усилию.
Характерным свойством воды является текучесть, с которой мы сталкиваемся постоянно. Вязкость жидкости обратно пропорциональна ее текучести. Между отдельными молекулами возникает сила трения, и чтобы сдвинуть их с места, необходимо приложить усилие. Такое явление получило в науке название «динамическая вязкость воды», которую можно увеличить, если в воде растворить какие-либо вещества. Это могут быть различные соли. Динамическую вязкость воды еще называют абсолютной, ее можно узнать с помощью произведения плотности жидкости на ее кинематическое сопротивление.
Такая пониженная текучесть потока, где линейная скорость под воздействием давления сдвига в 1 ньютон на метр квадратный имеет градиент один метр в секунду на одном метре расстояния, перпендикулярного к плоскости сдвига, является единицей измерения абсолютной (динамической) вязкости. Ее измеряют при помощи коэффициента динамической вязкости (μ, η). Например, в морской воде, где присутствуют неорганические соединения, сопротивление воды намного выше, чем у пресной. Это можно почувствовать, даже плавая в ней: если сравнить воду Азовского и Средиземного моря, то во втором варианте человек быстрее научится плавать, так как там вода более соленая.
Ее измеряют при помощи коэффициента динамической вязкости (μ, η). Например, в морской воде, где присутствуют неорганические соединения, сопротивление воды намного выше, чем у пресной. Это можно почувствовать, даже плавая в ней: если сравнить воду Азовского и Средиземного моря, то во втором варианте человек быстрее научится плавать, так как там вода более соленая.
Что представляет собой кинематическая вязкость воды?
В физике известно два вида жидкости — ньютоновская и неньютоновская. Течение первого вида подлежит описанию согласно законам вязкого трения Ньютона. При этом, соответственно, меняется название коэффициента пропорциональности. Кинематическая вязкость воды при 20 градусах по Цельсию составляет 1,006*10 6 м 2 /с.
Существуют специализированные таблицы со значениями кинематического сопротивления жидкости. Они изменяются при разных показателях температуры при атмосферном давлении 760 мм.рт.ст. Значения, в которых выражена вязкость воды, представлены в них в диапазоне температуры от 0 до 350 °С. Если нагреть эту жидкость больше 100 °С, ее кинематическое сопротивление дается на линии насыщения. Эти значения важны при различных температурах. Без них не обойтись при вычислении величины числа Рейнольдса, которое соответствует определенному режиму течения жидкости или газа.
Если нагреть эту жидкость больше 100 °С, ее кинематическое сопротивление дается на линии насыщения. Эти значения важны при различных температурах. Без них не обойтись при вычислении величины числа Рейнольдса, которое соответствует определенному режиму течения жидкости или газа.
При сравнительном анализе разных жидкостей, подчиненных закону Ньютона, например, крови или масел, доказано, что вода имеет меньшую вязкость. Она обладает большими показателями сопротивления в сравнении с органическими жидкостями.
Уравнение кинематической вязкости воды
Мера кинематического сопротивления жидкости — это коэффициент кинематической вязкости воды. Его, как и любую физическую величину, также можно вычислить. Он выражен отношением динамической вязкости к плотности:
ν = μ/ρ, где
- μ — динамическая вязкость в Н*с/м 2 ;
- ρ — плотность в кг/м 3 ;
- ν — кинематическое сопротивление в м 2 /c.
Естественно то, что вязкость меняется, как и агрегатные состояния вещества. Такие научные данные используются в авиа- и судостроении и некоторых других отраслях промышленности.
Такие научные данные используются в авиа- и судостроении и некоторых других отраслях промышленности.
Что происходит с водой при повышении температуры?
Затрудненная текучесть жидкости меняется с увеличением или уменьшением температуры, то есть коэффициент кинематической вязкости воды и динамический показатель не являются стабильными. Следовательно, коэффициенты сопротивления соленой и пресной воды разные.
Так как все значения этих коэффициентов невозможно запомнить, есть специализированные таблицы, где определена вязкость воды при температуре различных уровней. Данными пользуются в теории и на практике.
Как определить вязкость жидкости?
Вискозиметр специализируется на измерении этой характеристики воды с помощью таких методов:
- метод падающего шарика;
- истечение жидкости через капилляр;
- определение сопротивления с помощью ротационных вискозиметров.
Определяя коэффициент вязкости воды, на практике больше используют относительные методики, а не абсолютные, что позволяет пренебречь в расчетах константами приборов. Измерения сначала выполняют для стандартной жидкости, а потом для исследуемой.
Измерения сначала выполняют для стандартной жидкости, а потом для исследуемой.
От чего зависит вязкость?
Эта характеристика зависит от природы вещества. Если по форме различные частицы жидкости отличаются от сферической, при этом изменяя коэффициент вязкости, то сопротивление такого вещества значительно возрастает и уже не вычисляется согласно уравнению Ньютона. Палочкообразная, листочкообразная форма молекул растворов встречается в разнообразных гелях. Их сопротивление возрастает в связи с тем, что их частицы-мицеллы образуют сетчатую структуру-каркас, внутри которого находится жидкость.
Меняет значение и кинематическая вязкость воды, нагреваясь и охлаждаясь. При повышении температуры она становится меньше. Другими словами, вода при нагревании становится менее сопротивляемой, а при максимальном охлаждении проявляется высокая вязкость воды.
Вопрос:
Здравствуйте! Вы не можете подсказать, нигде не могу найти, какая вязкость у соленой воды плотностью 1,15-1,2 г/см 3 при низких и отрицательных температурах? Например при -20 градусах Цельсия? Заранее спасибо. Руслан
Руслан
Ответ:
Здравствуйте, уважаемый, Руслан!
Динамический коэффициент вязкости воды в сильной степени зависит от температуры, но почти не зависит от давления. Значение этого коэффициента для пресной воды, полученное опытным путем для t°С = 0°С, μ = 1,793·10 3 Па·с. При расчете динамического коэффициента вязкости применяют эмпирическую формулу Пуазейля:
μ = 0,000183/(1 + 0,0337t + 0,000221t 2),
где t — температура воды.
Динамический коэффициент вязкости соленой воды незначительно отличается от коэффициента вязкости пресной воды. Например, при t = 20°С и S = 25‰ он равен 1,052·10 -3 Па·с, а для пресной воды — 1,003·10 -3 Па·с, т. е. больше примерно на 5%.
Следует отметить, что во многие расчетные формулы входит отношение динамического коэффициента вязкости μ к плотности жидкости ρ, носящее название кинематического коэффициента вязкости (кинематическая вязкость):
ν = μ/ρ
Значения коэффициентов вязкости существенно уменьшаются с повышением температуры.
Вязкость жидкостей может быть определена и вискозиметром. Существует несколько типов таких приборов. В самом простом полевом вискозиметре, основанном на принципе истечения, в воронку наливается, например, исследуемый раствор объемом 500 см 3 , вязкость которого следует установить. Измеряются температура и время истечения из воронки исследуемого раствора Т р; затем наливается в воронку дистиллированная вода при такой же температуре (обычно 20°С) и определяется время ее истечения Т в. Отношение
Есть относительная вязкость (для вязких жидкостей она всегда больше 1).
Вязкость воды уменьшается при увеличении температуры весьма существенно: так, при увеличении температуры воды от 0 до 100 0 С вязкость уменьшается примерно в 8 раз. При нормальном атмосферном давлении для определения кинематического коэффициента вязкости воды в зависимости от температуры составлена таблице.
Значение v м 2 /с для воды в зависимости от температуры
| t°C | 0 | 2 | 4 | 6 | 8 |
| 0 | 179 | 167 | 157 | 147 | 138 |
| 10 | 131 | 124 | 117 | 112 | 106 |
| 20 | 101 | 96 | 92 | 87 | 84 |
| 30 | 80 | 75 | 72 | 69 | 67 |
| 40 | 66 | 62 | 60 | 58 | 56 |
| 50 | 56 | 52 | 51 | 49 | 48 |
Кроме того, вязкость жидкости зависит и от давления.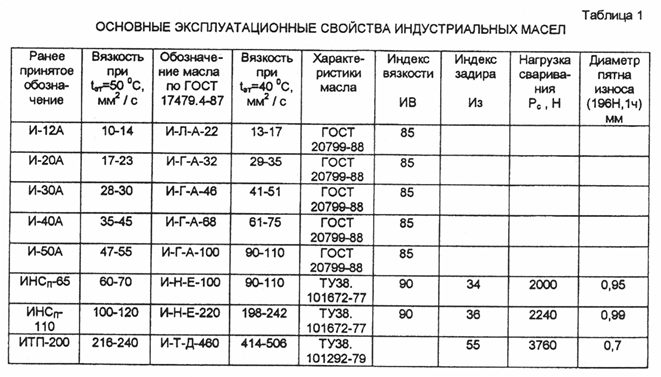 При давлении до 2·10 7 Па изменение вязкости воды незначительно и часто в расчетах не учитывается.
При давлении до 2·10 7 Па изменение вязкости воды незначительно и часто в расчетах не учитывается.
Справочные данные по зависимости вязкости воды от температуры приведены в следующих справочниках:
Ривкин С.Л. Теплофизические свойства воды www.oglibrary.ru/data/demo/6263/62630003.html
Справочник химика Никольского Б.П. lib.mexmat.ru/books/12114
Физические свойства воды
Плотность воды при её различной температуре
| Температура | Плотность |
| о С | кг/м 3 |
| 0 | 999,9 |
| 5 | 1000 |
| 10 | 999,7 |
| 20 | 998,2 |
| 30 | 995,7 |
| 40 | 992,2 |
| 50 | 988,1 |
| 60 | 983,2 |
| 70 | 977,8 |
| 80 | 971,8 |
| 90 | 965,3 |
| 100 | 958,4 |
Динамическая и кинематическая вязкость воды при её различной температуре
| Температура | Динамическая вязкость | Кинематическая вязкость |
| о С | (Н. c / м 2) x 10 -3 c / м 2) x 10 -3 | (м 2 / с) x 10 -6 |
| 0 | 1,787 | 1,787 |
| 5 | 1,519 | 1,519 |
| 10 | 1,307 | 1,307 |
| 20 | 1,002 | 1,004 |
| 30 | 0,798 | 0,801 |
| 40 | 0,653 | 0,658 |
| 50 | 0,547 | 0,658 |
| 60 | 0,467 | 0,475 |
| 70 | 0,404 | 0,413 |
| 80 | 0,355 | 0,365 |
| 90 | 0,315 | 0,326 |
| 100 | 0,282 | 0,294 |
Основные физические свойства воды при её различной температуре
| Температура | Плотность | Удельная теплоёмкость, C p | Коэффициент температурного линейного расширения | Число Прандтля |
| о С | кг/м 3 | кДж / (кг.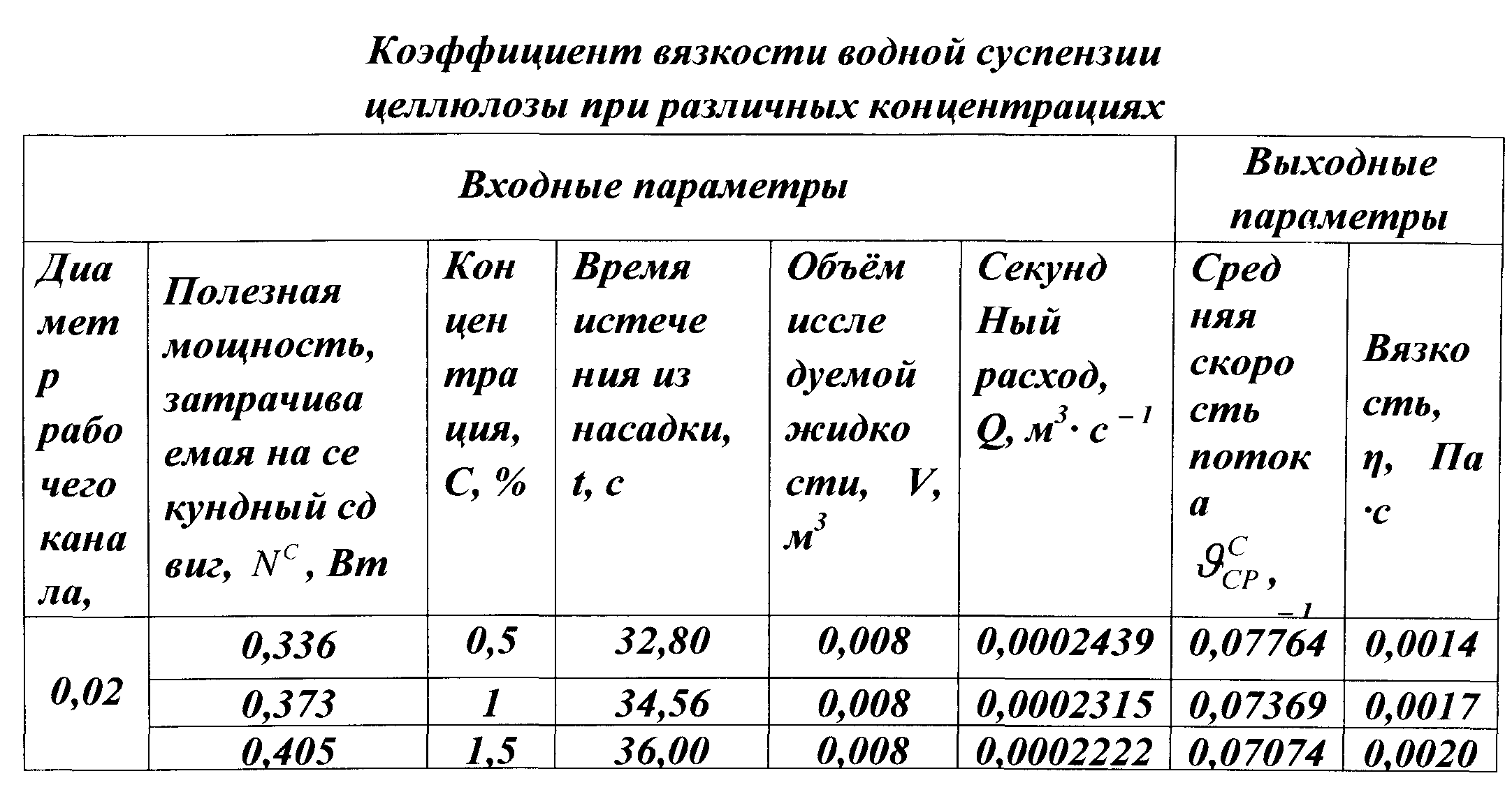 К) К) | (1 / K) x 10 3 | — |
| 0 | 999,9 | 4,217 | -0,07 | 13,67 |
| 20 | 998,2 | 4,182 | 0,207 | 7,01 |
| 40 | 992,1 | 4,179 | 0,385 | 4,34 |
| 60 | 983,2 | 4,185 | 0,523 | 2,99 |
| 80 | 971,8 | 4,197 | 0,643 | 2,23 |
| 100 | 958,4 | 4,216 | 0,752 | 1,75 |
Таблица 15.5
Кинематическая вязкость некоторых жидкостей при 20° (Hadgman C.D., 1965)
Вода препятствует продвижению пловца. В гидродинамике для расчета движения жидкости используют число Рейнольдса. Число Рейнольдса — это безразмерная величина , где — плотность и вязкость жидкости, и — скорость ее движения относительно тела и а — некоторая длина.
Правило, согласно которому строение потока около тел одной и той же формы одинаково, если одинаково число Рейнольдса, неприменимо в тех случаях, когда речь идет о поведении жидкости около ее свободной поверхности.
Число Рейнольдса удобно выражать как величина, называемая кинематической вязкостью.
Во многих случаях трудно измерять силы, которые действуют на тело, движущееся в жидкости. В этой связи для экспериментов используют аэродинамические и гидродинамические трубы.
Лобовое сопротивление. При движении какого-нибудь тела в жидкости, на него действует сила, задерживающая его движение. Эту силу называют лобовым сопротивлением. Величина ее зависит от природы жидкости и от размеров, формы и скорости движущегося тела.
Как показали эксперименты в аэродинамических трубах, лобовое сопротивление тела или различных тел одной и той же формы можно определить по формуле где Д — лобовое сопротивление, р — плотность жидкости, и — скорость движения жидкости относительно тела, А — характеристическая площадь и С д — величина, называемая коэффициентом лобового сопротивления, которая зависит от формы тела и от числа Рейнольдса.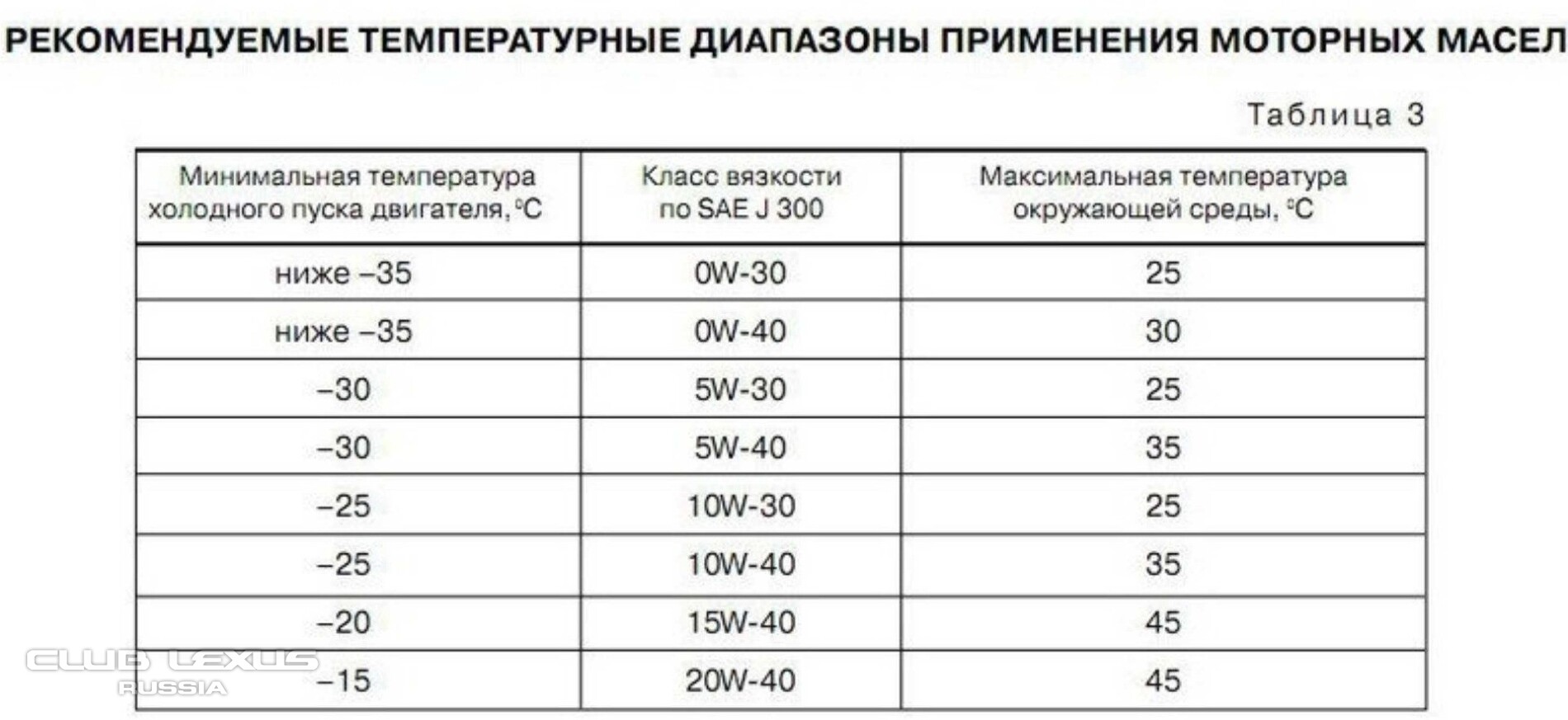
К сожалению, не существует единого определения А, которое было бы удобным при любой форме тела. Используются следующие площади:
1) лобовая площадь, т. е. площадь проекции тела на плоскость, перпендикулярно направлению потока. В случае цилиндра, имеющего высоту h и радиус г, лобовая площадь будет равна πr 2 , если ось цилиндра параллельна потоку, и 2rh, если она перпендикулярна ему;
2) площадь наибольшей проекции, т. е. проекции по тому направлению, по которому площадь ее будет наибольшей; эту величину используют, когда имеют дело с обтеканием профиля крыла; по сравнению с лобовой площадью она имеет то преимущество, что не изменяется при наклоне профиля;
3) суммарная поверхность тела. Следует помнить, что в случае тонкой пластинки это будет суммарная площадь обеих ее сторон.
Если есть сомнения, то важно указать, какая именно из этих площадей была использована при вычислении коэффициента С
На рис. 15.34 приведены кривые зависимости коэффициента лобового сопротивления С д от числа Рейнольдса для тел различной формы.
Все коэффициенты были вычислены на основе лобовой площади.
Число Рейнольдса для всех тел, кроме диска, определялось обычным способом по длине, измеренной в направлении потока; для диска же его определяли по диаметру, хотя он расположен перпендикулярно потоку.
В связи с отсутствием работы по лобовому сопротивлению у пловцов, мы приводим данные Т.О. Lang, K.S. Norris (1966), R. Alexander (1968) полученные при изучении дельфинов. Было найдено, что при коротких «бросках» дельфин может развивать скорость до 830 см/с (около 16 узлов), а со скоростью 610 см/с (около 12 узлов) способен плыть примерно в течение 1 мин. Дельфин (Turbiopsgilli) имел длину 191 см, так что число Рейнольдса при первой из этих скоростей составляло 830·191 /0,01 = 1,6·10 7 . Профиль дельфина хорошо обтекаем. Кожа очень гладкая и лишена волос. Все указывает на малую величину лобового сопротивления.
Рис. 15.34. Зависимость коэффициента лобового сопротивления от числа Рейнольдса для диска, расположенного перпендикулярно направлению своего движения; для удлиненного цилиндра, движущегося перпендикулярно своей оси; для шара и для тела обтекаемой формы, движущегося вдоль своей оси (по Р. Александер, 1970)
Александер, 1970)
Попробуем оценить величину лобового сопротивления для дельфина, плывущего со скоростью 830 см/с и мощность, развиваемую его мышцами. Лобовая площадь у дельфина длиной 191 см, вероятно, составляет около 1100 см 2 . Коэффициенты лобового сопротивления для обтекаемых тел при числе Рейнольдса около 1,6-10 7 близки к 0,055. Подставив эти величины в уравнение
Мы найдем, что лобовое сопротивление у нашего дельфина составляет примерно 1 /2 (830) 2 ·1100·0,055 = 2,0-10 7 дин. Мощность равна сопротивлению, умноженному на скорость, т. е. в данном случае 830·2,0·10 7 эрг/с, или 1660 Вт. Однако от мышц требуется большая мощность, так как КПД дельфина при плавании не может достигать 100%; поэтому она едва ли могла быть меньше 2000 Вт. Дельфин весит 89 кг, из которых на долю участвующих в плавании мышц приходится, вероятно, около 15 кг. Таким образом, мощность мышц должна составлять примерно 130 Вт/кг. Это в 3 раза больше максимальной мощности, которую могут развивать мышцы человека при работе на велоэргометре.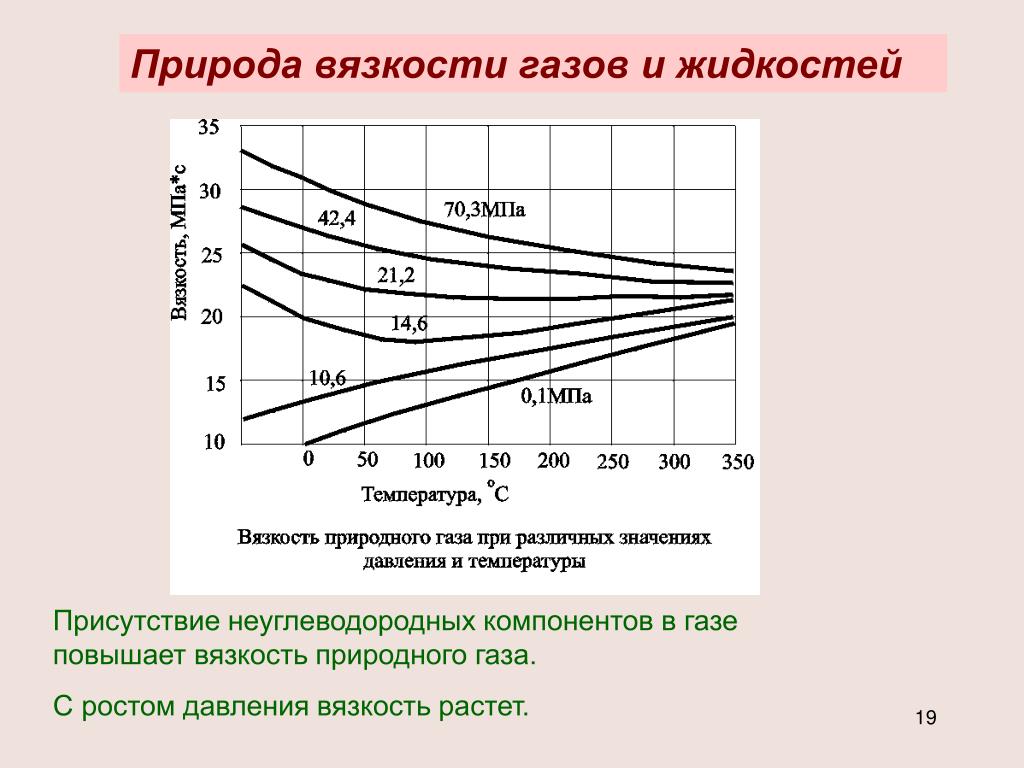
Лобовое сопротивление — не единственная гидродинамическая сила, действующая на тела, которые движутся в жидкости или находятся в потоке. По определению оно имеет то же направление, что и скорость движения жидкости относительно тела. Когда симметричное тело движется вдоль своей оси симметрии, действующая на него гидродинамическая сила направлена прямо и представляет собой лобовое сопротивление. Но когда симметричное тело движется под некоторым углом к оси симметрии, гидродинамическая сила действует под углом к его пути. Ее можно разложить на две составляющие, одна из которых направлена назад и представляет собой лобовое сопротивление, а другая действует под прямым углом к первой.
Энергетика пловца. Когда человек плывет, он сообщает некоторое количество энергии воде, чтобы продвинуться (проплыть) в ней. Это создает волну, которая в конечном счете потеряет всю сообщенную ей энергию в виде тепла, и поверхность воды снова станет спокойной. Затраченная таким образом при плавании энергия представляет собой совершенную работу плюс тепло, потерянное телом пловца.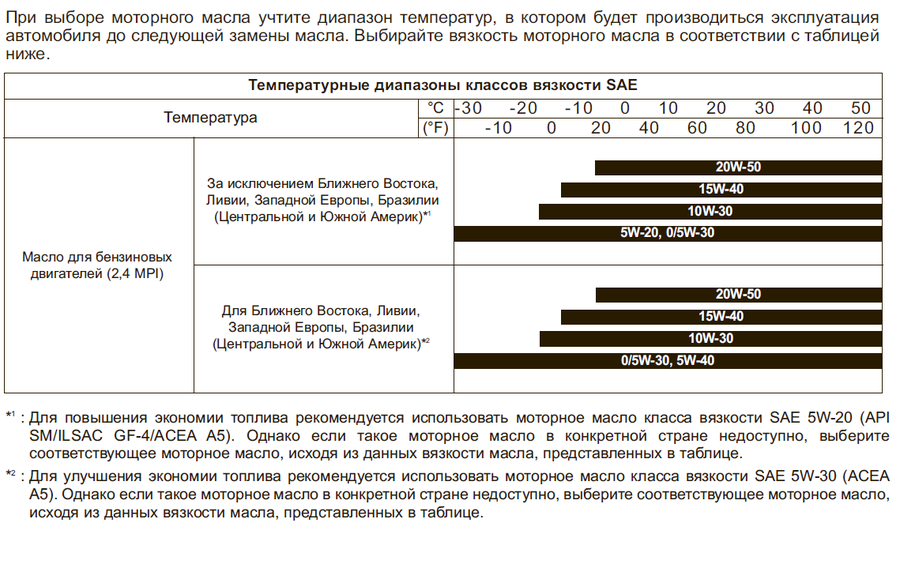
ОПРЕДЕЛЕНИЕ
Вязкостью называют один из видов явлений переноса. Она связана со свойством текучих веществ (газов и жидкостей), сопротивляться перемещению одного слоя относительно другого. Это явление вызывается движением частиц, которые составляют вещество.
Выделяют динамическую вязкость и кинематическую.
Рассмотрим движение газа, обладающего вязкостью как перемещение плоских параллельных слоев. Будем считать, что изменение скорости движения вещества происходит по направлению оси X, которая перпендикулярна к направлению скорости движения газа (рис.1).
В направлении оси Y скорость движения во всех точках одинакова. Значит, скорость является функцией . В таком случае, модуль силы трения между слоями газа (F), которая действует на единицу площади поверхности, которая разделяет два соседних слоя, описывается уравнением:
где — градиент скорости () по оси X. Ось X перепендикулярна направлению движения слоев вещества (рис.1).
Определение
Коэффициент (), входящий в уравнение (1) называется коэффициентом динамической вязкости (коэффициентом внутреннего трения). Он зависит от свойств газа (жидкости). численно равен количеству движения, которое переносится в единицу времени через площадку единичной площади при градиенте скорости равном единице, в направлении перпендикулярном площадке. Или численно равен силе, которая действует на единицу площади при градиенте скорости, равном единице.
Он зависит от свойств газа (жидкости). численно равен количеству движения, которое переносится в единицу времени через площадку единичной площади при градиенте скорости равном единице, в направлении перпендикулярном площадке. Или численно равен силе, которая действует на единицу площади при градиенте скорости, равном единице.
Внутренне трение — причина того, что для течения газа (жидкости) сквозь трубу необходима разность давлений. При этом, чем больше коэффициент вязкости вещества, тем больше должна быть разность давлений для придания заданной скорости течению.
Коэффициент кинематической вязкости обычно, обозначают . Он равен:
где — плотность газа (жидкости).
Коэффициент внутреннего трения газа
В соответствии с кинетической теорией газов коэффициент вязкости можно вычислить при помощи формулы:
где — средняя скорость теплового движения молекул газа, — средняя длина свободного пробега молекулы. Выражение (3) показывает, что при низом давлении (разреженный газ) вязкость почти не зависит от давления, так как Но такой вывод справедлив до момента, пока отношение длины свободного пробега молекулы к линейным размерам сосуда не станет приблизительно равным единице. При увеличении температуры вязкость газов обычно растет, так как
При увеличении температуры вязкость газов обычно растет, так как
Коэффициент вязкости жидкостей
Считая, что коэффициент вязкости определен силами взаимодействия молекул вещества, которые зависят от среднего расстояния между ними, то коэффициент вязкости определяют экспериментальной формулой Бачинского:
где — молярный объем жидкости, А и B — постоянные величины.
Вязкость жидкостей с ростом температуры уменьшается, при увеличении давления растет.
Формула Пуазейля
Коэффициент вязкости входит в формулу, которая устанавливает зависимость между объемом (V) газа, который протекает в единицу времени через сечение трубы и необходимой для этого разностью давлений ():
где — длина трубы, — радиус трубы.
Число Рейнольдса
Характер движения газа (жидкости) определяется безразмерным числом Рейнольдса ():
— величина, которая характеризует линейные размеры тела, обтекаемого жидкостью (газом).Единицы измерения коэффициента вязкости
Основной единицей измерения коэффициента динамической вязкости в системе СИ является:
1Па c=10 пуаз
Основной единицей измерения коэффициента кинематической вязкости в системе СИ является:
Примеры решения задач
ПРИМЕР 1
| Задание | Динамически вязкость воды равна Па с. Какая величина предельного диаметра трубы позволит течению воды остаться ламинарным, если за 1 с через поперечное сечение вытекает объем воды равный ? Какая величина предельного диаметра трубы позволит течению воды остаться ламинарным, если за 1 с через поперечное сечение вытекает объем воды равный ? |
| Решение | Условие ламинарности течения жидкости имеет вид: Где число Рейнольдса найдем по формуле: Скорость течения воды найдем как: В выражении (1.3) — высота водяного цилиндра, имеющего объем : По условию =1 с. Подставим в выражение для числа Рейнольдса скорость (1.4), имеем: Плотность воды при н.у. кг/м 3 . Проведем вычисления, получим: |
| Ответ | м |
ПРИМЕР 2
| Задание | Шарик, имеющий плотность и диаметр d всплывает в жидкости плотности со скоростью . Какова кинематическая вязкость жидкости? |
| Решение | Сделаем рисунок. |
Рассчитать смесь из смесей разной вязкости. Определение вязкости жидкости
Воспользуйтесь удобным конвертером перевода кинематической вязкости в динамическую онлайн. Поскольку соотношение кинематической и динамической вязкости зависит от плотности, то необходимо ее также указывать при расчете в калькуляторах ниже.
Поскольку соотношение кинематической и динамической вязкости зависит от плотности, то необходимо ее также указывать при расчете в калькуляторах ниже.
Плотность и вязкость следует указывать при одинаковой температуре.
Если задать плотность при температуре отличной от температуры вязкости повлечет некоторую ошибку, степень которой будет зависеть от влияния температуры на изменение плотности для данного вещества.
Калькулятор перевода кинематической вязкости в динамическую
Конвертер позволяет перевести вязкость с размерностью в сантистоксах [сСт] в сантипуазы [сП] . Обратите внимание, что численные значения величин с размерностями [мм2/с] и [сСт] для кинематической вязкости и [сП] и [мПа*с] для динамической — равны между собой и не требуют дополнительного перевода. Для других размерностей — воспользуйтесь таблицами ниже.
Динамическая вязкость, [сП]=[мПа*с]
Плотность, [кг/м3]
Если вы используете условную вязкость ее необходимо перевести в кинематическую.
 Для этого воспользуйтесь калькулятором .
Для этого воспользуйтесь калькулятором .Таблицы перевода размерностей вязкости
В случае, если размерность Вашей величины не совпадает с используемой в калькуляторе, воспользуйтесь таблицами перевода.
Выберете размерность в левом столбце и умножьте свою величину на множитель, находящийся в ячейке на пересечении с размерностью в верхней строчке.
Табл. 1. Перевод размерностей кинематической вязкости ν
Табл. 2. Перевод размерностей динамической вязкости μ
Себестоимость добычи нефти
Связь динамической и кинематической вязкости
Вязкость жидкости определяет способность жидкости сопротивляться сдвигу при ее движении, а точнее сдвигу слоев относительно друг друга. Поэтому на производствах, где требуется перекачка различных сред, важно точно знать вязкость перекачиваемого продукта и правильно подбирать насосное оборудование.
В технике встречаются два вида вязкости.
- Кинематическая вязкость чаще используется в паспорте с характеристиками жидкости.

- Динамическая используется в инженерных расчетах оборудования, научно-исследовательских работах и т.д.
Перевод кинематической вязкости в динамическую производят с помощью формулы, указанной ниже, через плотность при заданной температуре:
v — кинематическая вязкость,
n — динамическая вязкость,
p — плотность.
Таким образом, зная ту или иную вязкость и плотность жидкости можно выполнить пересчет одного вида вязкости в другой по указанной формуле или через конвертер выше.
Измерение вязкости
Понятия для этих двух типов вязкости присуще только жидкостям в связи с особенностями способов измерения.
Измерение кинематической вязкости используют метод истечения жидкости через капилляр (например используя прибор Уббелоде). Измерение динамической вязкости происходит через измерение сопротивление движения тела в жидкости (например сопротивление вращению погруженного в жидкость цилиндра).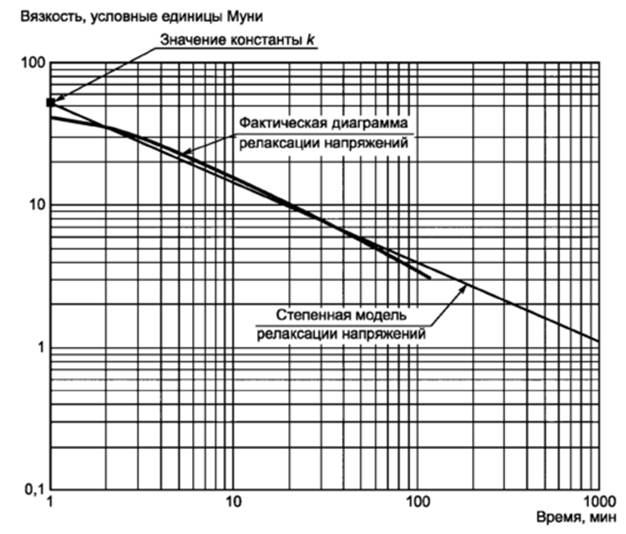
От чего зависит значение величины вязкости?
Вязкость жидкости зависит в значительной мере от температуры. С увеличением температуры вещество становится более текучим, то есть менее вязким. Причем изменение вязкости, как правило, происходит достаточно резко, то есть нелинейно.
Поскольку расстояние между молекулами жидкого вещества намного меньше, чем у газов, у жидкостей уменьшается внутреннее взаимодействие молекул из-за снижения межмолекулярных связей.
Кстати, прочтите эту статью тоже: Асфальт
Форма молекул и их размер, а также взаимоположение и взаимодействие могут определять вязкость жидкости. Также влияет их химическая структура.
Например, для органических соединений вязкость возрастает при наличии полярных циклов и групп.
Для насыщенных углеводородов — рост происходит при «утяжелении» молекулы вещества.
ВАМ БУДЕТ ИНТЕРЕСНО:
Нефтеперерабатывающие заводы России Особенности переработки тяжелой нефти Перевод объемного расхода в массовый и обратно Перевод баррелей нефти в тонны и обратно Трубчатые печи: конструкция и характеристики
Вязкость является важнейшей физической константой, характеризующей эксплуатационные свойства котельных и дизельных топлив, нефтяных масел, ряда других нефтепродуктов. По значению вязкости судят о
возможности распыления и прокачиваемости нефти и нефтепродуктов.
По значению вязкости судят о
возможности распыления и прокачиваемости нефти и нефтепродуктов.
Различают динамическую, кинематическую, условную и эффективную (структурную) вязкость.
Динамической (абсолютной) вязкостью [μ ], или внутренним трением, называют свойства реальных жидкостей оказывать сопротивление сдвигающим касательным усилиям. Очевидно, это свойство проявляется при движении жидкости. Динамическая вязкость в системе СИ измеряется в [Н·с/м 2 ]. Это сопротивление, которое оказывает жидкость при относительном перемещении двух ее слоев поверхностью 1 м 2 , находящихся на расстоянии 1 м друг от друга и перемещающихся под действием внешней силы в 1 Н со скоростью 1 м/с. Учитывая, что 1 Н/м 2 = 1 Па, динамическую вязкость часто выражают в [Па·с] или [мПа·с]. В системе СГС (CGS) размерность динамической вязкости — [дин·с/м 2 ]. Эта единица называется пуазом (1 П = 0,1 Па·с).
Переводные множители для расчета динамической [μ ] вязкости.
| Единицы | Микропуаз (мкП) | Сантипуаз (сП) | Пуаз ([г/см·с]) | Па·с ([кг/м·с]) | кг/(м·ч) | кг·с/м 2 |
| Микропуаз (мкП) | 1 | 10 -4 | 10 -6 | 10 7 | 3,6·10 -4 | 1,02·10 -8 |
| Сантипуаз (сП) | 10 4 | 1 | 10 -2 | 10 -3 | 3,6 | 1,02·10 -4 |
| Пуаз ([г/см·с]) | 10 6 | 10 2 | 1 | 10 3 | 3,6·10 2 | 1,02·10 -2 |
| Па·с ([кг/м·с]) | 10 7 | 10 3 | 10 | 1 3 | 3,6·10 3 | 1,02·10 -1 |
| кг/(м·ч) | 2,78·10 3 | 2,78·10 -1 | 2,78·10 -3 | 2,78·10 -4 | 1 | 2,84·10 -3 |
| кг·с/м 2 | 9,81·10 7 | 9,81·10 3 | 9,81·10 2 | 9,81·10 1 | 3,53·10 4 | 1 |
Кинематической вязкостью [ν ] называется величина, равная отношению динамической вязкости жидкости [μ ] к ее плотности [ρ ] при той же
температуре: ν = μ/ρ.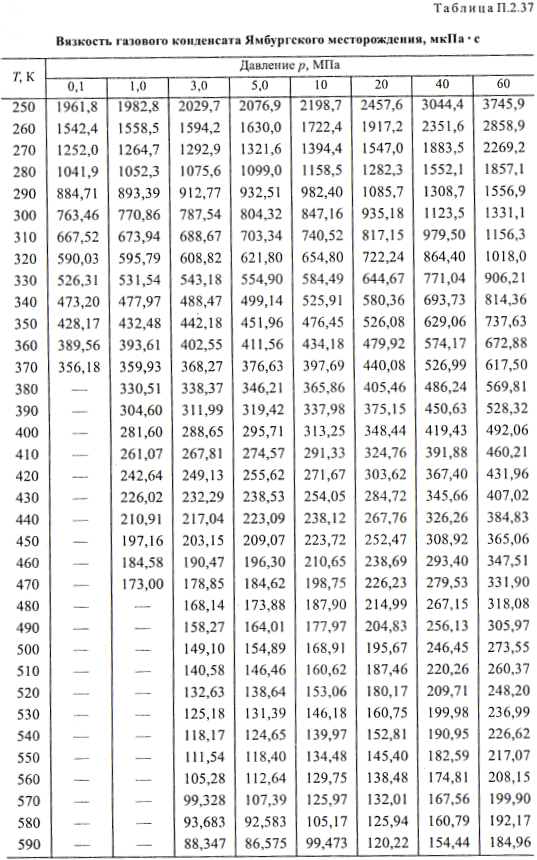 Единицей кинематической вязкости является [м 2 /с] — кинематическая вязкость такой жидкости, динамическая вязкость которой равна 1 Н·с/м 2 и
плотность 1 кг/м 3 (Н = кг·м/с 2). В системе СГС (CGS) кинематическая вязкость
выражается в [см 2 /с]. Эта единица называется стоксом (1 Ст = 10 -4 м 2 /с; 1 сСт = 1 мм 2 /с).
Единицей кинематической вязкости является [м 2 /с] — кинематическая вязкость такой жидкости, динамическая вязкость которой равна 1 Н·с/м 2 и
плотность 1 кг/м 3 (Н = кг·м/с 2). В системе СГС (CGS) кинематическая вязкость
выражается в [см 2 /с]. Эта единица называется стоксом (1 Ст = 10 -4 м 2 /с; 1 сСт = 1 мм 2 /с).
Переводные множители для расчета кинематической [ν ] вязкости.
| Единицы | мм 2 /с (сСт) | см 2 /с (Ст) | м 2 /с | м 2 /ч |
| мм 2 /с (сСт) | 1 | 10 -2 | 10 -6 | 3,6·10 -3 |
| см 2 /с (Ст) | 10 2 | 1 | 10 -4 | 0,36 |
| м 2 /с | 10 6 | 10 4 | 1 | 3,6·10 3 |
| м 2 /ч | 2,78·10 2 | 2,78 | 2,78·10 4 | 1 |
Нефти и нефтепродукты часто характеризуются условной вязкостью , за которую принимается отношение времени истечения через калиброванное отверстие стандартного вискозиметра
200 мл нефтепродукта при определенной температуре [t ] ко времени истечения 200 мл дистиллированной воды при температуре 20°С.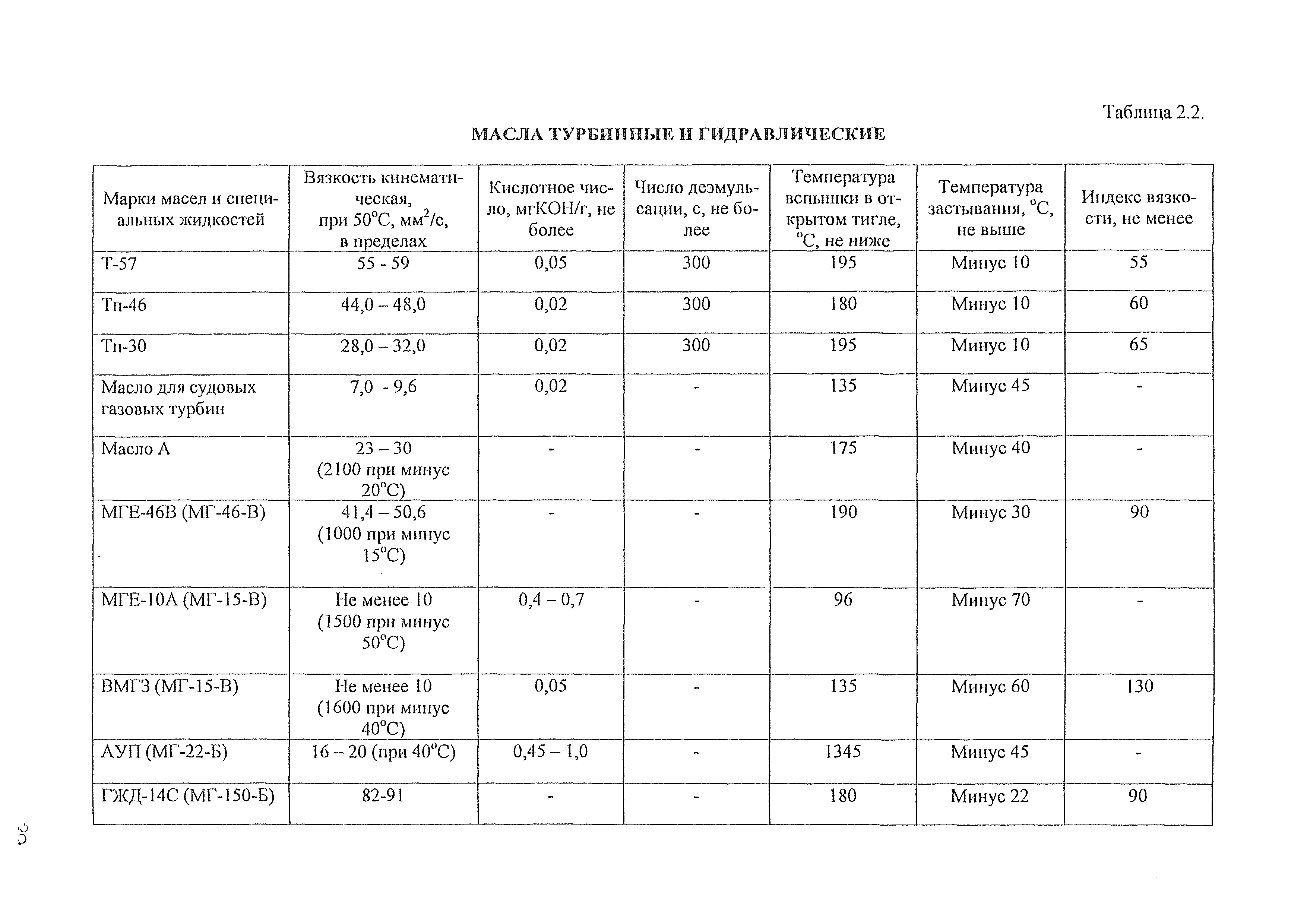 Условная вязкость при температуре [t ] обозначается знаком ВУ,
и выражается числом условных градусов.
Условная вязкость при температуре [t ] обозначается знаком ВУ,
и выражается числом условных градусов.
Условная вязкость измеряется в градусах ВУ (°ВУ) (если испытание проводится в стандартном вискозиметре по ГОСТ 6258-85), секундах Сейболта и секундах Редвуда (если испытание проводится на вискозиметрах Сейболта и Редвуда).
Перевести вязкость из одной системы в другую можно при помощи номограммы .
В нефтяных дисперсных системах в определенных условиях в отличие от ньютоновских жидкостей вязкость является переменной величиной, зависящей от градиента скорости сдвига. В этих случаях нефти и нефтепродукты характеризуются эффективной или структурной вязкостью:
Для углеводородов вязкость существенно зависит от их химического состава: она повышается с увеличением молекулярной массы и температуры кипения. Наличие боковых разветвлений в молекулах алканов и
нафтенов и увеличение числа циклов также повышают вязкость. Для различных групп углеводородов вязкость растет в ряду алканы — арены — цикланы.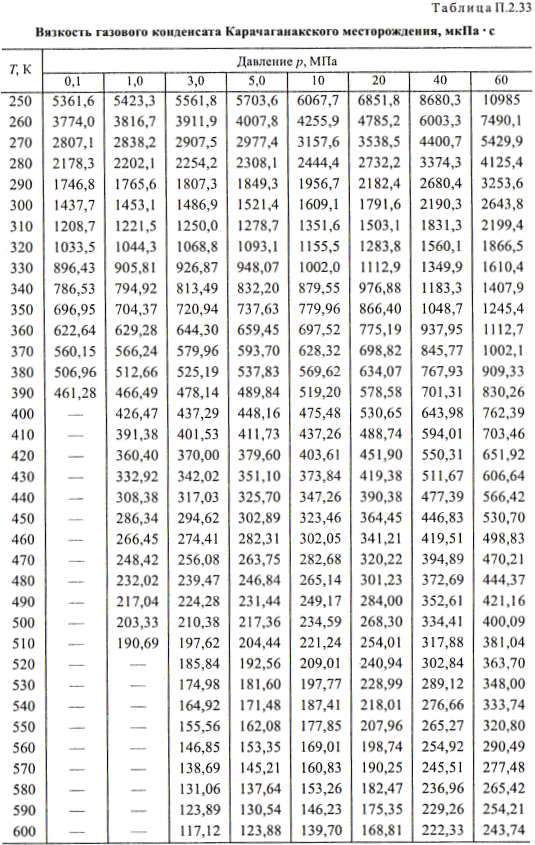
Для определения вязкости используют специальные стандартные приборы — вискозиметры, различающиеся по принципу действия.
Кинематическая вязкость определяется для относительно маловязких светлых нефтепродуктов и масел с помощью капиллярных вискозиметров, действие которых основано на текучести жидкости через капилляр по ГОСТ 33-2000 и ГОСТ 1929-87 (вискозиметр типа ВПЖ, Пинкевича и др.).
Для вязких нефтепродуктов измеряется условная вязкость в вискозиметрах типа ВУ, Энглера и др. Истечение жидкости в этих вискозиметрах происходит через калиброванное отверстие по ГОСТ 6258-85.
Между величинами условной °ВУ и кинематической вязкости существует эмпирическая зависимость:
Вязкость наиболее вязких, структурированных нефтепродуктов определяется на ротационном вискозиметре по ГОСТ 1929-87. Метод основан на измерении усилия, необходимого для вращения внутреннего
цилиндра относительно наружного при заполнении пространства между ними испытуемой жидкостью при температуре t .
Кроме стандартных методов определения вязкости иногда в исследовательских работах используются нестандартные методы, основанные на измерении вязкости по времени падения калибровочного шарика между метками или по времени затухания колебаний твердого тела в испытуемой жидкости (вискозиметры Гепплера, Гурвича и др.).
Во всех описанных стандартных методах вязкость определяют при строго постоянной температуре, поскольку с ее изменением вязкость существенно меняется.
Зависимость вязкости от температуры
Зависимость вязкости нефтепродуктов от температуры является очень важной характеристикой как в технологии переработки нефти (перекачка, теплообмен, отстой и т. д.), так и при применении товарных нефтепродуктов (слив, перекачка, фильтрование, смазка трущихся поверхностей и т. д.).
С понижением температуры вязкость их возрастает. На рисунке приведены кривые изменения вязкости в зависимости от температуры для различных смазочных масел.
Общим для всех образцов масел является наличие областей температур, в которых наступает резкое повышение вязкости.
Существует много различных формул для расчета вязкости в зависимости от температуры, но наиболее употребляемой является эмпирическая формула Вальтера:
Дважды логарифмируя это выражение, получаем:
По данному уравнению Е. Г. Семенидо была составлена номограмма на оси абсцисс которой для удобства пользования отложена температура, а на оси ординат — вязкость.
По номограмме можно найти вязкость нефтепродукта при любой заданной температуре, если известна его вязкость при двух других температурах. В этом случае значение известных вязкостей соединяют прямой и продолжают ее до пересечения с линией температуры. Точка пересечения с ней отвечает искомой вязкости. Номограмма пригодна для определения вязкости всех видов жидких нефтепродуктов.
Для нефтяных смазочных масел очень важно при эксплуатации, чтобы вязкость как можно меньше зависела от температуры, поскольку это обеспечивает хорошие смазывающие свойства масла в широком интервале
температур, т.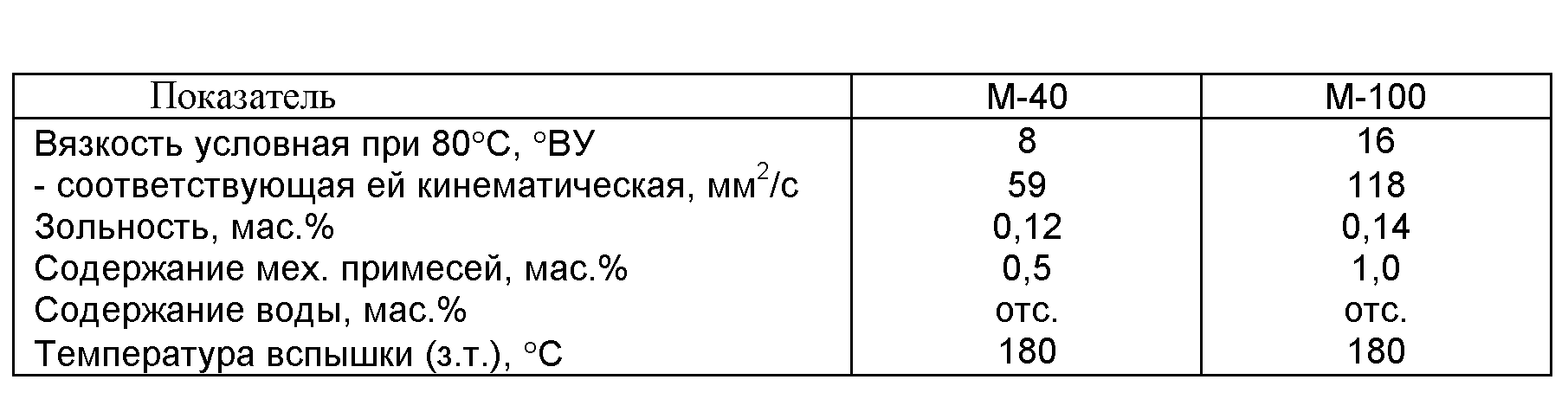 е. в соответствии с формулой Вальтера это означает, что для смазочных масел, чем ниже коэффициент В, тем выше качество масла. Это свойство масел называется индексом вязкости ,
который является функцией химического состава масла. Для различных углеводородов по-разному меняется вязкость от температуры. Наиболее крутая зависимость (большая величина В) для ароматических
углеводородов, а наименьшая — для алканов. Нафтеновые углеводороды в этом отношении близки к алканам.
е. в соответствии с формулой Вальтера это означает, что для смазочных масел, чем ниже коэффициент В, тем выше качество масла. Это свойство масел называется индексом вязкости ,
который является функцией химического состава масла. Для различных углеводородов по-разному меняется вязкость от температуры. Наиболее крутая зависимость (большая величина В) для ароматических
углеводородов, а наименьшая — для алканов. Нафтеновые углеводороды в этом отношении близки к алканам.
Существуют различные методы определения индекса вязкости (ИВ).
В России ИВ определяют по двум значениям кинематической вязкости при 50 и 100°С (или при 40 и 100°С — по специальной таблице Госкомитета стандартов).
При паспортизации масел ИВ рассчитывают по ГОСТ 25371-97, который предусматривает определение этой величины по вязкости при 40 и 100°С. По этому методу согласно ГОСТ (для масел с ИВ меньше 100) индекс вязкости определяется формулой:
Для всех масел с ν 100 ν, ν 1 и ν 3 ) определяют по таблице ГОСТ 25371-97 на основе ν 40 и ν 100 данного масла. Если масло более вязкое (ν 100 > 70 мм 2 /с), то величины, входящие в формулу, определяют по специальным
формулам, приведенным в стандарте.
Если масло более вязкое (ν 100 > 70 мм 2 /с), то величины, входящие в формулу, определяют по специальным
формулам, приведенным в стандарте.
Значительно проще определять индекс вязкости по номограммам .
Еще более удобная номограмма для нахождения индекса вязкости разработана Г. В. Виноградовым. Определение ИВ сводится к соединению прямыми линиями известных величин вязкости при двух температурах. Точка пересечения этих линий соответствует искомому индексу вязкости.
Индекс вязкости — общепринятая величина, входящая в стандарты на масла во всех странах мира. Недостатком показателя индекса вязкости является то, что он характеризует поведение масла лишь в интервале температур от 37,8 до 98,8°С.
Многими исследователями было подмечено, что плотность и вязкость смазочных масел до некоторой степени отражают их углеводородный состав. Был предложен соответствующий показатель, связывающий
плотность и вязкость масел и названный вязкостно-массовой константой (ВМК). Вязкостно-массовая константа может быть вычислена по формуле Ю. А. Пинкевича:
Вязкостно-массовая константа может быть вычислена по формуле Ю. А. Пинкевича:
В зависимости от химического состава масла ВМК его может быть от 0,75 до 0,90, причем, чем выше ВМК масла, тем ниже его индекс вязкости.
В области низких температур смазочные масла приобретают структуру, которая характеризуется пределом текучести, пластичности, тиксотропностью или аномалией вязкости, свойственными дисперсным системам. Результаты определения вязкости таких масел зависят от их предварительного механического перемешивания, а также от скорости истечения или от обоих факторов одновременно. Структурированные масла, так же как и другие структурированные нефтяные системы, не подчиняются закону течения ньютоновских жидкостей, согласно которому изменение вязкости должно зависеть только от температуры.
Масло с неразрушенной структурой имеет значительно большую вязкость, чем после ее разрушения. Если понизить вязкость такого масла путем разрушения структуры, то в спокойном состоянии эта структура восстановится и вязкость примет первоначальное значение. Способность системы самопроизвольно восстанавливать свою структуру называется тиксотропией . С увеличением скорости течения, точнее градиента скорости (участок кривой 1), структура разрушается, в связи с чем вязкость вещества снижается и доходит до определенного минимума. Этот минимум вязкости сохраняется на одном уровне и при последующем возрастании градиента скорости (участок 2) до появления турбулентного потока, после чего вязкость вновь нарастает (участок 3).
Зависимость вязкости от давления
Вязкость жидкостей, в том числе и нефтепродуктов, зависит от внешнего давления. Изменение вязкости масел с повышением давления имеет большое практическое значение, так как в некоторых узлах трения могут возникать высокие давления.
Зависимость вязкости от давления для некоторых масел иллюстрируется кривыми, вязкость масел с повышением давления изменяется по параболе. При давлении Р она может быть выражена формулой:
В нефтяных маслах меньше всего с повышением давления изменяется вязкость парафиновых углеводородов и несколько больше нафтеновых и ароматических. Вязкость высоковязких нефтепродуктов с увеличением давления повышается больше, чем вязкость маловязких. Чем выше температура, тем меньше изменяется вязкость с повышением давления.
При давлениях порядка 500 — 1000 МПа вязкость масел возрастает настолько, что они теряют свойства жидкости и превращаются в пластичную массу.
Для определения вязкости нефтепродуктов при высоком давлении Д.Э.Мапстон предложил формулу:
На основе этого уравнения Д.Э.Мапстоном разработана номограмма , при пользовании которой известные величины, например ν 0 и Р , соединяют прямой линией и отсчет получают на третьей шкале.
Вязкость смесей
При компаундировании масел часто приходится определять вязкость смесей. Как показали опыты, аддитивность свойств проявляется лишь в смесях двух весьма близких по вязкости компонентов. При большой разности вязкостей смешиваемых нефтепродуктов, как правило, вязкость меньше, чем вычисленная по правилу смешения. Приближенно вязкость смеси масел можно рассчитать, если заменить вязкости компонентов их обратной величиной — подвижностью (текучестью) ψ см :
Для определения вязкости смесей можно также пользоваться различными номограммами. Наибольшее применение нашли номограмма ASTM и вискозиграмма Молина-Гурвича . Номограмма ASTM базируется на формуле Вальтера. Номограмма Молина-Гуревича составлена на основании экспериментально найденных вязкостей смеси масел А и В, из которых А обладает вязкостью °ВУ 20 = 1,5, а В — вязкостью °ВУ 20 = 60. Оба масла смешивались в разных соотношениях от 0 до 100% (об.), и вязкость смесей устанавливалась экспериментально. На номограмме нанесены значения вязкости в уел. ед. и в мм 2 /с.
Вязкость газов и нефтяных паров
Вязкость углеводородных газов и нефтяных паров подчиняется иным, чем для жидкостей, закономерностям. С повышением температуры вязкость газов возрастает. Эта закономерность удовлетворительно описывается формулой Сазерленда:
Вязкость определяет внутреннее сопротивление жидкости силе, которая направлена на то, чтобы заставить эту жидкость течь. Вязкость бывает двух видов — абсолютная и кинематическая. Первую обычно используют в косметике, медицине и кулинарии, а вторую — чаще в автомобильной промышленности.
Абсолютная вязкость и кинематическая вязкость
Абсолютная вязкость жидкости, также называемая динамической, измеряет сопротивление силе, заставляющей ее течь. Она измеряется независимо от свойств вещества. Кинематическая вязкость , наоборот, зависит от плотности вещества. Для определения кинематической вязкости абсолютную вязкость делят на плотность этой жидкости.
Кинематическая вязкость зависит от температуры жидкости, поэтому помимо самой вязкости необходимо указывать при какой температуре жидкость приобретает такую вязкость. Вязкость машинного масла обычно измеряют при температурах 40° C (104° F) и 100° C (212° F). Во время замены масла в автомобилях автомеханики часто используют свойство масел становиться менее вязкими при повышении температуры. Например, чтобы удалить максимальное количество масла из двигателя, его предварительно прогревают, в результате масло вытекает легче и быстрее.
Ньютоновские и неньютоновские жидкости
Вязкость изменяется по-разному, в зависимости от вида жидкости. Различают два вида — ньютоновские и неньютоновские жидкости. Ньютоновскими называются жидкости, вязкость которых изменятся независимо от деформирующей ее силы. Все остальные жидкости — неньютоновские. Они интересны тем, что деформируются с разной скоростью в зависимости от сдвигового напряжения, то есть, деформация происходит с большей или, наоборот, меньшей скоростью в зависимости от вещества и от силы, которая давит на жидкость. Вязкость также зависит от этой деформации.
Кетчуп — классический пример неньютоновской жидкости. Пока он в бутылке, почти невозможно заставить его выйти наружу под действием небольшой силы. Если мы, наоборот, приложим большую силу, например, начнем сильно трясти бутылку, то кетчуп легко из нее вытечет. Так, большое напряжение делает кетчуп текучим, а маленькое — почти не влияет на его текучесть. Это свойство присуще только неньютоновским жидкостям.
Другие неньютоновские жидкости, наоборот, становятся более вязкими с увеличением напряжения. Пример такой жидкости — смесь крахмала и воды. Человек может спокойно пробежать через бассейн, ею наполненный, но начнет погружаться, если остановится. Это происходит потому, что в первом случае сила, действующая на жидкость, намного больше, чем во втором. Существуют неньютоновские жидкости и с другими свойствами — например в них вязкость изменяется не только в зависимости от общего количества напряжения, но и от времени, в течение которого на жидкость действует сила. Например, если общее напряжение вызвано большей силой и действует на тело в течение короткого промежутка времени, а не распределено на более длительный отрезок с меньшей силой, то жидкость, например мед, становится менее вязкой. То есть, если интенсивно мешать мед, он станет менее вязким по сравнению с размешиванием его с меньшей силой, но в течение более длительного времени.
Вязкость и смазка в технике
Вязкость — важное свойство жидкостей, которое используется в повседневной жизни. Наука, изучающая текучесть жидкостей, называется реологией и посвящена ряду тем, связанных с этим явлением, включая вязкость, так как вязкость напрямую влияет на текучесть разных веществ. Реология обычно изучает как ньютоновские, так и неньютоновские жидкости.
Индикаторы вязкости моторного масла
Производство машинного масла происходит при строгом соблюдении правил и рецептуры, чтобы вязкость этого масла была именно такой, какая необходима в той или иной ситуации. Перед продажей производители контролируют качество масла, а механики в автосалонах проверяют его вязкость перед тем, как залить в двигатель. В обоих случаях измерения проходят по-разному. При производстве масла обычно измеряют его кинематическую вязкость, а механики, наоборот, измеряют абсолютную вязкость, а потом переводят ее в кинематическую. При этом используют разные устройства для измерения. Важно знать разницу между этими измерениями и не путать кинематическую вязкость с абсолютной, так как они неодинаковы.
Чтобы получить более точные измерения, изготовители машинных масел предпочитают использовать кинематическую вязкость. Измерители кинематической вязкости также намного дешевле измерителей абсолютной вязкости.
Для автомобилей очень важно, чтобы вязкость масла в двигателе соответствовала норме. Чтобы детали автомобиля служили как можно дольше, необходимо по возможности уменьшить трение. Для этого их покрывают толстым слоем моторного масла. Масло должно быть достаточно вязким, чтобы как можно дольше оставаться на трущихся поверхностях. С другой стороны, оно должно быть достаточно жидким, чтобы проходить по масляным каналам без заметного уменьшения скорости потока даже в холодную погоду. То есть, даже при низких температурах масло должно оставаться не очень вязким. К тому же, если масло слишком вязкое, то трение между подвижными деталями будет высоким, что приведет к увеличению расхода топлива.
Моторное масло — это смесь разных масел и добавок, например антивспенивающих и моющих присадок. Поэтому знать вязкость самого масла недостаточно. Необходимо также знать конечную вязкость продукта, и при необходимости изменять ее, если она не соответствует принятым стандартам.
Смена масла
По мере использования, процент добавок в моторном масле уменьшается и само масло становится грязным. Когда загрязнение слишком велико и добавленные в него присадки сгорели, масло становится непригодным, поэтому его необходимо регулярно менять. Если этого не делать, то грязь может засорить масляные каналы. Вязкость масла изменится и не будет соответствовать стандартам, вызывая различные проблемы, например забитые масляные каналы. Некоторые ремонтные мастерские и производители масла советуют менять его каждые 5 000 километров (3 000 миль), но производители автомобилей и некоторые автомеханики утверждают, что замены масла после каждых 8 000 до 24 000 километров (от 5 000 до 15 000 миль) вполне достаточно, если автомобиль исправен и в хорошем состоянии. Замена каждые 5 000 километров подходит для более старых двигателей, и сейчас советы о такой частой замене масла — рекламный ход, заставляющий автолюбителей покупать больше масла и пользоваться услугами сервисных центров чаще, чем это на самом деле необходимо.
По мере того, как конструкция двигателей улучшается, увеличивается и расстояние, которое может проехать автомобиль без замены масла. Поэтому чтобы решить, когда стоит залить в автомобиль новое масло, руководствуйтесь информацией в инструкции по эксплуатации или сайтом производителя автомобиля. В некоторых транспортных средствах также установлены датчики, которые следят за состоянием масла — их тоже удобно использовать.
Как правильно выбрать моторное масло
Чтобы не ошибиться с выбором вязкости, при выборе масла нужно учитывать для какой погоды и для каких условий оно предназначено. Некоторые масла предназначены для работы в холодных или, наоборот, в жарких условиях, а некоторые хороши в любую погоду. Масла также делят на синтетические, минеральные и смешанные. Последние состоят из смеси минеральных и синтетических компонентов. Самые дорогие масла — синтетические, а самые дешевые — минеральные, так как их производство дешевле. Синтетические масла становятся все более популярными благодаря тому, что они дольше служат, и их вязкость остается неизменной в большом интервале температур. Покупая синтетическое моторное масло, важно проверить, будет ли ваш фильтр служить так же долго, как и масло.
Изменение вязкости моторного масла в связи с изменением температуры происходит в разных маслах по-разному, и эта зависимость выражается индексом вязкости, который обычно указывают на упаковке. Индекс равный нулю — для масел, вязкость которых наиболее зависима от температуры. Чем меньше вязкость зависит от температуры, тем лучше, поэтому автомобилисты предпочитают масла с высоким индексом вязкости, особенно в холодном климате, где разница температур между горячим двигателем и холодным воздухом очень большая. На данный момент индекс вязкости синтетических масел выше, чем минеральных. Смешанные масла находятся посредине.
Чтобы вязкость масла дольше оставалась неизменной, то есть, чтобы повысить индекс вязкости, в масло нередко добавляют различные присадки. Часто эти присадки сгорают до рекомендованного срока замены масла, то есть масло становится менее пригодным к употреблению. Водители, использующие масла с такими добавками, вынуждены либо регулярно проверять, достаточна ли концентрация этих добавок в масле, либо часто менять масло, либо довольствоваться маслом со сниженными качествами. То есть, масло с высоким индексом вязкости не только дорогое, но к тому же требует постоянного контроля.
Масло для других транспортных средств и механизмов
Требования к вязкости масел для других транспортных средств часто совпадают с требованиями к автомобильными маслам, но иногда они отличаются. Например, требования для масла, которое используют для велосипедной цепи, другие. Владельцам велосипедов обычно приходится выбирать между невязким маслом, которое легко наносить на цепь, например из аэрозольного распылителя, и вязким, которое хорошо и долго держится на цепи. Вязкое масло эффективно уменьшает силу трения и не смывается с цепи во время дождя, но быстро загрязняется, так как в открытую цепь попадают пыль, сухая трава и другая грязь. С невязким маслом нет таких проблем, но его приходится часто наносить заново, а невнимательные или неопытные велосипедисты иногда не знают этого и портят цепь и шестерни.
Измерение вязкости
Для измерения вязкости используют устройства, называемые реометрами или вискозиметрами. Первые применяют для жидкостей, чья вязкость изменяется в зависимости от окружающих условий, а вторые работают с любыми жидкостями. Некоторые реометры представляют собой цилиндр, который вращается внутри другого цилиндра. В них измеряют силу, с которой жидкость во внешнем цилиндре вращает внутренний цилиндр. В других реометрах жидкость наливают на пластину, помещают в нее цилиндр, и измеряют силу, с которой жидкость действует на цилиндр. Существуют и другие типы реометров, но принцип их работы похож — они измеряют силу, с которой жидкость действует на подвижный элемент этого устройства.
Вискозиметры измеряют сопротивление жидкости, которая перемещается внутри измерительного прибора. Для этого жидкость проталкивают через тонкую трубку (капилляр) и измеряют сопротивление жидкости движению по трубке. Это сопротивление можно узнать, измерив время, которое требуется, чтобы жидкость продвинулась на определенное расстояние в трубке. Время преобразуют в вязкость с помощью вычислений или таблиц, имеющихся в документации для каждого устройства.
Вязкость жидкостей
Динамическая вязкость , или коэффициент динамической вязкости ƞ (ньютоновской), определяется формулой:
η = r / (dv/dr),
где r – сила вязкого сопротивления (на единицу площади) между двумя соседними слоями жидкости, направленная вдоль их поверхности, а dv/dr– градиент их относительной скорости, взятый по направлению, перпендикулярному к направлению движения. Размеренность динамической вязкости ML -1 T -1 , ее единицей в системе СГС служит пуаз (пз) = 1г/см*сек=1дин*сек/см 2 =100 сантипуазам (спз)
Кинематическая вязкость определяется отношением динамической вязкости ƞ к плотности жидкости p. Размерность кинематической вязкости L 2 T -1 , ее единицей в системе СГС служит стокс (ст) = 1 см 2 /сек=100 сантистоксам (сст).
Текучесть φ является величиной, обратной динамической вязкости. Последняя для жидкостей уменьшается с понижением температуры приблизительно по закону φ=А+В/Т, где А и В являются характеристическими постоянными, а Т обозначает абсолютную температуру. Величины А и В для большого количества жидкостей были даны Бэррером.
Таблица вязкость воды
Данные Бингхема и Джексона, выверенные по национальному стандарту в США и Великобритании на 1 июля 1953 года, ƞ при 20 0 С=1,0019 сантипуаза.
Температура, 0 С | Температура, 0 С | ||
Таблица вязкость различных жидкостей Ƞ, спз
Жидкость | |||||||||
Бромбензол | |||||||||
Кислота муравьиная | |||||||||
Кислота серная | |||||||||
Кислота уксусная | |||||||||
Масло касторовое | |||||||||
Масло прованское | |||||||||
Сероуглерод | |||||||||
Спирт метиловый | |||||||||
Спирт этиловый | |||||||||
Углекислота (жидкая) | |||||||||
Углерод четыреххлористый | |||||||||
Хлороформ | |||||||||
Этилацетат | |||||||||
Этилформиат | |||||||||
Эфир этиловый |
Относительная вязкость некоторых водных растворов (таблица)
Концентрация растворов предполагается нормальным, который содержит в 1л один грамм-эквивалент растворенного вещества. Вязкости даны по отношению к вязкости воды при той же температуре.
Вещество | Температура, °С | Относительная вязкость | Вещество | Температура, °С | Относительная вязкость |
Кальций хлористый | |||||
Аммоний хлористый | Кислота серная | ||||
Калий йодистый | Кислота соляная | ||||
Калий хлористый | Натр едкий |
Таблица вязкость водных растворов глицерина
Удельный вес 25°/25°С | Весовой процент глицерина | |||
Вязкость жидкостей при высоких давлениях по Бриджмену
Таблица относительная вязкость воды при высоких давлениях
Давление кгс/см 3 | ||||
Таблица относительная вязкость различных жидкостей при высоких давлениях
Ƞ=1 при 30 ° С и давление 1 кгс/см 2
Жидкость | Температура, ° С | Давление кгс/см 2 | |||
Сероуглерод | |||||
Спирт метиловый | |||||
Спирт этиловый | |||||
Эфир этиловый | |||||
Вязкость твердых тел (ПЗ)
Таблица вязкость газов и паров
Динамическая вязкость газов обычно выражается в микропуазах (мкпз). Согласно кинетической теории вязкость газов должна не зависеть от давления и изменяться пропорционально квадратному корню из абсолютной температуры. Первый вывод оказывается в общем правильным, исключением являются очень низкие и очень высокие давления; второй вывод требует некоторых поправок. Для изменения ƞ в зависимости от абсолютной температуры Т наиболее часто применяется формула:
Газ или пар | Постоянная Сёзерлэнда, С | ||||||||
Закись азота | |||||||||
Кислород | |||||||||
Пары воды | |||||||||
Сернистый газ | |||||||||
Спирт этиловый | |||||||||
Углекислота | |||||||||
Углерода окись | |||||||||
Хлороформ | |||||||||
Таблица вязкость некоторых газов при высоких давлениях (мкпз)
Температура, 0 С | Давление в атмосферах | |||||
Углекислота | ||||||
Для определения кинематической вязкости вискозиметр подбирают таким образом, чтобы время течения нефтепродукта было не менее 200 с.T = Bh(T1 – T2)
- B – коэффициент температурного расширения рабочей жидкости термометра:
- для ртутного термометра – 0,00016
- для спиртового – 0,001
- h – высота выступающего столбика рабочей жидкости термометра, выраженная в делениях шкалы термометра
- T1 – заданная температура в термостате, оС
- T2 – температура окружающего воздуха вблизи середины выступающего столбика, оС.
Определение времени истечения повторяют несколько раз. В соответствии с ГОСТ 33-82 число измерений устанавливают в зависимости от времени истечения: пять измерений – при времени истечения от 200 до 300 с; четыре – от 300 до 600 с и три – при времени истечения свыше 600 с. При проведении отсчетов необходимо следить за постоянством температуры и отсутствием пузырьков воздуха.
Для подсчета вязкости определяют среднее арифметическое значение времени истечения. При этом учитывают только те отсчеты, которые отличаются не более чем на ± 0,3 % при точных и на ± 0,5 % при технических измерениях от среднего арифметического.
Учебная работа по физике «Вязкость жидкости»
Конкурс
«Пермский университет – школьникам: физико-математические науки»
16 летс. Березовка
МБОУ «Березовская СОШ№2»,
9класс
ФИО участника:
Радостев Тимофей Николаевич
Почтовый адрес:
617570 Пермский край,с.Березовка,ул.Труда,4а кв.18
Название работы:
Горизонты науки
Телефон:
89194654115
e-mail:
Научный руководитель:
Дёмина Галина Ивановна
Телефон:
89082630535
e-mail:
«Горизонты науки»
МБОУ «Берёзовская средняя
общеобразовательная школа №2»,
ученик 9 «в» класса.
Руководитель: Дёмина Г.И.
учитель физики высшей кв. кат.
МОУ «Берёзовская средняя
общеобразовательная школа №2».
с. Березовка 2015г.
Оглавление
Введение…………………………………………………………………………………………………….3
Глава 1. Гидродинамика. Уравнение Бернулли .. ……………………….………6
Глава 2. Ламинарное и турбулентное течение жидкости ..…….………….…..10
Глава 3. Коэффициент вязкости. Закон Ньютона ……. ………………………12
Глава 4. Вязкость крови …………………………….……………………..….…14
Глава 5. Неньютоновская жидкость………………………………………….…16
Глава 6. Метод Стокса для определения коэффициента вязкости…………………………………………………………………………..17
Глава 7.Практическая часть……………………………………………….………20
Определение давления жидкости внутри трубки переменного сечения (экспериментальное подтверждение уравнения Бернулли).
Определение коэффициента вязкости глицерина методом Стокса.
Заключение……………………………………………………………………….25
Список литературы……………………………………………………………….27
Введение
Многим известно имя английского ученого – И.Ньютона. Прежде всего, говорят о Ньютоне как о создателе классической механики. Этот человек открыл закон всемирного тяготения, открыл законы разложения белого света и выдвинул корпускулярную теорию света, открыл закон охлаждения нагретого тела, сконструировал один из первых термометров, впервые построил отражательный телескоп.
Именно Ньютон разработал могучий метод математического исследования природы, что оказало огромное влияние на все последующее развитие физики как науки.
При подготовке сообщения о Ньютоне только в одной книге я встретил информацию о том, что он открыл закон сопротивления движению в вязкой жидкости. Меня заинтересовал этот вопрос, и в своей работе я решил изучить закономерности движения жидкости, закон сопротивления движению в вязкой жидкости, подробнее познакомиться со свойством жидкости – ее вязкостью.
Цель работы: изучение закономерностей движения жидкости.
Задачи:
Найти в различных источниках информации законы движения жидкости, сведения о свойствах жидкостей, в частности ее вязкости;
Изучить особенности ньютоновской и неньютоновской жидкостей;
Исследовать явления, происходящие с неньютоновской жидкостью;
Определить экспериментальным способом вязкость жидкости;
Показать практическое проявление движущихся потоков жидкости;
В книге Ф.М. Дягилева «Из истории физики и жизни ее творцов» рассказывается о жизни и творчестве выдающихся физиков. В ней отмечено, что выдающимся трудом И. Ньютона являются «Математические начала натуральной философии». Во второй части «Начал» (иногда так называют) Ньютон рассмотрел силы сопротивления среды при движении в ней тел, гидро- и аэродинамику, простейшие случаи вихревых движений. Эта информация побудила меня изучить движение жидкостей и закономерности, происходящие в ней.
В учебнике И.К. Кикоина «Физика, учебник для 9 класса» раскрывается суть закона Бернулли. В учебнике Г.Я. Мякишева «Физика. Механика.10кл. учебник для углубленного изучения физики» рассмотрены основы гидродинамики: виды движений в жидкости, течение вязкой жидкости, существование силы сопротивления при движении тел в жидкостях. В справочнике школьника Т.И. Трофимовой :Физика от А до Я кратко, но доступно дается материал по вязкости жидкости: определение вязкости жидкости, формула силы внутреннего трения, зависимость вязкости от температуры.
В книге Майорова А.Н. «Физика для любознательных, или о чем не узнаешь на уроке» приведены примеры проявления уравнения Бернулли.
В пособии Г.Е.Кирко «Лабораторные работы» описан метод Стокса для определения коэффициента вязкости.
На сайтах http://www.youtube.com/watch?v=f2XQ97XHjVwhttp://studopedia.ru содержится информация о удивительной жидкости — неньютоновской жидкости.
С движущимися потоками жидкости мы часто встречаемся в технике, быту и в природе. По трубам водопровода течет вода в домах, в машинах подается масло для смазки, по трубам нефтепроводов течет нефть. Кровообращение у человека и животных – это движение крови по трубам – кровеносным сосудам. Даже движение воды в реках можно считать движением жидкости по трубам, если считать русло реки «трубой».
Раздел физики, изучающий движения жидкостей, взаимодействие движущихся жидкостей с твердыми телами называется гидродинамикой.
В общем случае движения жидкости нужно учитывать наличие сил внутреннего трения или вязкости. Вязкость – одно из важнейших явлений, наблюдающихся при движении реальной жидкости. Явления, связанные с вязкостью усложняют исследование движения жидкости. Поэтому полезно вначале отвлечься от усложнений, вносимых ею в картину движения жидкостей и изучить закономерности для идеальной жидкости. Идеальная жидкость — жидкость, вязкостью которой можно пренебречь.
Основным законом гидродинамики является закон (уравнение) Бернулли.
Гидродинамика. Уравнение Бернулли.
Закон (уравнение) Бернулли является следствием закона сохранения энергии для потока идеальной (то есть без внутреннего трения) жидкости:
ρ — плотность жидкости,
v — скорость потока
h — высота, на которой находится рассматриваемый элемент жидкости,
p — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
g — ускорение свободного падения.
Описать движение жидкости трудновато. Хотя гидродинамика основана на трех хорошо знакомых в механике законах сохранения массы, импульса и энергии, их формулировка в данной теме немного сложнее. Например, определение закона сохранения массы обычно выглядит так: масса системы тел остается неизменной. Для жидкости, текущей в трубе, этот закон используется в форме (называемой уравнением неразрывности ):
υS=const
Здесь – υ скорость жидкости, S – площадь сечения трубы, по которой течет жидкость. Сформулировать этот закон можно так: сколько вливается жидкости в трубу, столько должно и выливаться, если условия течения не изменяются. Согласно уравнению неразрывности, скорость жидкости в узких местах трубки больше, чем в широких.
Каково распределение давления в движущейся жидкости? Можно определить его экспериментально. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены стеклянные открытые сверху измерительные трубки. При стационарном течении (движение жидкости называется стационарным, если во всех точках пространства скорости элементов жидкости не меняются со временем) жидкость в каждой измерительной трубке поднимется до определенной высоты. По высоте столба жидкости в измерительных трубках можно судить о её давлении на стенки горизонтальной трубки. Опыт показывает, что в широких местах трубки, давление больше, чем в узких. Но чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:
при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и, наоборот, меньше в тех местах, где скорость течения больше.
Зависимость давления идеальной жидкости от скорости ее стационарного течения и перепада высоты была установлена в математической форме Даниилом Бернулли в 1783 году. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости.
Уравнение Бернулли просто объясняет множество явлений, происходящих в жидкости.
1) Осенью 1912г. океанский пароход «Олимпик» плыл в открытом море, а почти параллельно ему, на расстоянии 100 метров, проходил с большой скоростью другой корабль, гораздо меньший, броненосный крейсер «Гаук». Вдруг произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь неведомой силе, повернулось носом к большому кораблю и , и не слушаясь руля, двинулось прямо на него. «Гаук» врезался носом в бок «Олимпика». Удар был так силен, что. «Гаук» проделал в борту «Олимпика» большую пробоину. Случай столкновения двух кораблей рассматривался в морском суде. Капитана «Олимпика» обвинили в том, что он не дал команду пропустить броненосец. Не сразу поняли, как можно объяснить происшедшее.
Теперь капитаны морских и речных судов прекрасно знакомы с коварным проявлением уравнения Бернулли. Если два корабля идут параллельным курсом слишком близко один к другому, возникает гидродинамическая сила, толкающая их друг к другу, в результате чего может произойти кораблекрушение. Формула Бернулли позволяет понять, почему возникает эта сила: относительная скорость воды между судами будет больше, чем снаружи, давление воды на корабли в пространстве между ними окажется ниже, чем извне. Перепад давлений по разные стороны кораблей создает силу, толкающую их друг к другу.
2) Закон Бернулли позволяет измерять скорость движения жидкости с помощью манометра – прибора для измерения давления.
3)С помощью уравнения Бернулли можно найти скорость истечения идеальной жидкости из отверстия, расположенного в сосуде на глубине h относительно поверхности жидкости. Если сосуд широкий, а отверстие мало, то скорости жидкости в сосуде малы. Ко всему потоку жидкости в целом можно применить уравнение Бернулли. В верхнем сечении у поверхности жидкости давление p 0 равно атмосферному, а скорость υ0 »0. В нижнем сечении «трубки» — в отверстии давление также равно атмосферному.
4)Ярким примером, где применяется уравнение Бернулли в настоящее время, является «брандспойт». Он устроен так, что его края разного диаметра. Большим диаметром брандспойт цепляется к шлангу по которому подается вода . Она проходит через брандспойт и выходит через отверстие с меньшим диаметром. Получается, проходит через трубку с переменным сечением, где и работает закон Бернулли. За счет этого удалось добиться того, что вода выходит из него с большей скоростью и струя бьет на большие расстояния. Что значительно помогает при тушении пожаров.
По видам движение делится на ламинарное и турбулентное.
Наиболее простым является ламинарное (без завихрений) движение жидкостей. Турбулентное движение наиболее часто встречается, но в реальных жидкостях очень сложно. До сих пор нет полной теории его, хотя проблемы турбулентности изучаются уже более ста лет.
Ламинарное и турбулентное течение жидкости.
Ламинарное (слоистое) – движение жидкости, при котором отдельные слои ее скользят друг относительно друга, не перемешиваясь. Турбулентное (вихревое) – движение жидкости, сопровождающееся перемешиванием ее различных слоев с образованием завихрений. Другими словами: если жидкость находится между двумя металлическими пластинами, то течение жидкости называется ламинарным, когда слой жидкости, контактирующий с подвижной металлической пластиной, имеет ту же скорость, что и эта пластина. Слой жидкости, расположенный ниже, перемещается немного медленнее, и скорость каждого последующего слоя немного меньше, чем предыдущего. При этом каждый слой жидкости скользит по-другому, и разные слои не перемешиваются.
В ламинарном потоке каждая частица жидкости следует по пути своей предыдущей частицы. Скорость течения в любой точке жидкости остается постоянной. Линии тока не пересекаются между собой. Энергия, сообщаемая жидкости для поддержания ее течения, используется, главным образом, на преодоление вязких сил между слоями жидкости.
Другой тип течения называется турбулентным. Турбулентное течение неустойчиво. Послойный характер течения жидкости нарушается. В потоке образуются местные завихрения, частицы перемещаются не только параллельно, но и перпендикулярно оси трубки, непрерывно перемешиваясь. Линии тока становятся искривленными. Скорость частиц, пересекающих конкретную точку жидкости, не является постоянной по направлению и величине: она изменяется со временем. Описание турбулентного потока должно быть статистическим: с точки зрения средних величин. Для турбулентного течения необходима большая энергия, чем для ламинарного, поскольку при турбулентном течении существенно возрастает внутреннее трение между частицами жидкости.
Характер течения будет определяться целым рядом факторов: вязкость жидкости, сечение трубы, скорость течения и плотность жидкости.
На любой малый объем жидкости в потоке действует ускоряющая сила F1 и сила вязкого трения F2 . Английский физик Рейнольдс исследовал условия, при которых течение является ламинарным или турбулентным. Переход из ламинарного течения в турбулентное зависит от значения безразмерной величины, называемой числом Рейнольдса. Число Рейнольдса для жидкости, текущей в цилиндрической трубке определяется уравнением: Re = vDρ/η,
где v — средняя скорость потока, D — диаметр трубки, η — вязкость, и ρ — плотность жидкости.
Критическая величина числа Рейнольдса для цилиндрических трубок, при котором ламинарное течение становится турбулентным — 2000 — 2400.
Критическая скорость — скорость жидкости, при превышении которой ламинарное течение переходит в турбулентное. Течение крови в сосудах является ламинарным (за исключением аорты). В аорте наблюдается турбулентное течение крови во время физической работы, которая приводит к существенному увеличению скорости течения крои. Поток крови также может стать турбулентным в артериях при уменьшении площади их поперечного сечения вследствие патологических процессов. Причиной этого феномена является повышение скорости течения крови.
Течение крови в сосудах носит в норме ламинарный характер, небольшая турбулентность наблюдается вблизи клапанов сердца. Турбулентность в крови можно обнаружить по характерным шумам и использовать в диагностике заболеваний.
Если при движении существенным является трение, то вся теория гидродинамики усложняется. При движении жидкости нужно учитывать наличие сил внутреннего трения или вязкости. Вязкость – одно из важнейших явлений, наблюдающихся при движении реальной жидкости. Явления, связанные с вязкостью усложняют исследование движения жидкости.
Коэффициент вязкости. Закон Ньютона.
Вязкость – это одно из явлений переноса, свойство жидкости оказывать сопротивление перемещению одной их части относительно другой.
Всем реальным жидкостям в той или иной степени присуща вязкость, или внутреннее трение. При течении реальной жидкости между ее слоями возникают силы трения. Эти силы получили название сил внутреннего трения или вязкости. Вязкость – это трение между перемещаемыми относительно друг друга слоями жидкости. Силы вязкости (внутреннего трения) направлены по касательной к соприкасающимся слоям жидкости и противодействуют перемещению этих слоев относительно друг друга. Они тормозят слой с большей скоростью и ускоряют медленный слой. Можно указать две основные причины, обусловливающие вязкость:
во-первых, силы взаимодействия между молекулами соприкасающихся слоев, движущихся с различными скоростями;
во-вторых, переход молекул из слоя в слой и связанный с этим перенос импульса.
Вследствие этих причин слои взаимодействуют друг с другом, медленный слой ускоряется, быстрый замедляется. В жидкостях ярче выражена первая причина, в газах – вторая.
Ньютон установил, что сила трения между двумя слоями жидкости прямо пропорциональна площади соприкосновения слоев и величине:
— величина, показывающая, как быстро меняется скорость при переходе от слоя к слою.
Эта формула (1)называется формулой Ньютона для вязкого трения. Коэффициент пропорциональности получил название коэффициента вязкости (внутреннего трения).
Жидкости, для которых выполняется формула Ньютона (1), называют ньютоновскими. Для таких жидкостей коэффициент вязкости зависит только от температуры. К ньютоновским жидкостям можно отнести плазму крови.
Для многих реальных жидкостей соотношение (1) строго не выполняется. Такие жидкости называют неньютоновскими. Для них коэффициент вязкости зависит от температуры, давления и ряда других величин. К таким жидкостям относятся жидкости с крупными сложными молекулами, например, цельная кровь, водный раствор крахмала.
В системе СИ единицей измерения коэффициента вязкости является
(паскаль – секунда),
в СГС – системе коэффициент вязкости измеряется в (пуазах), причем
.
Как отмечено выше, жидкости различают: ньютоновские, неньютоновские. Из биологических к ньютоновским жидкостям относится кроме плазмы крови лимфа.
Закон Ньютона для жидкости применяется в медицине – в лабораториях определяют вязкость крови для выяснения на содержание эритроцитов, общего содержания белка и соотношения его фракций в плазме, а также содержания в крови углекислоты. Повышение вязкости отмечается при сгущении крови и некоторых видах лейкозов (эритремии, миелофиброзах), понижение — при анемиях.
Вязкость крови
Кровь является взвесью клеток крови в жидкости сложного состава, называемой плазмой. Различают красные клетки крови (эритроциты), белые клетки крови (лейкоциты) и тромбоциты. Плазма — водный раствор электролитов, белков, питательных веществ, продуктов метаболизма и т.п. Объем крови в организме составляет почти 7% объема человеческого тела. Эритроциты занимают около 45 % объема крови, а другие клетки крови — менее чем 1%. Относительный объем клеток крови и плазмы определяют с помощью прибора гематокрита. Это же название используют для определения результатов анализа.
Кровь является более плотной и вязкой, чем вода. В среднем относительная вязкость крови составляет почти 4,5 (3,5-5,4). Относительная вязкость плазмы — 2,2 (1,9 — 2,6). Вязкость крови измеряется в лаборатории с помощью специального прибора — медицинского вискозиметра. Кровь является неньютоновской жидкостью. Но при такой скорости течения, которая поддерживается в сосудах кровеносной системы, вязкие свойства крови можно рассматривать, как для ньютоновских жидкостей. А плазма крови – ньютоновская жидкость.
Вязкость крови зависит, главным образом, от концентрации эритроцитов и меньше — от концентрации белков плазмы. Она зависит также от скорости течения крови. Если скорость течения крови уменьшается, эритроциты собираются в специфические скопления, так называемые монетные столбики. Это приводит к повышению вязкости крови. Такой феномен может наблюдаться в мелких кровеносных сосудах, где скорость течения крови небольшая.
Однако существует физиологический механизм, который способствует уменьшению вязкости крови в небольших сосудах, называемый эффектом Фареуса-Линдквиста. Этот эффект объясняется ориентацией эритроцитов вдоль оси сосуда. Эритроциты, формируя цилиндрический осевой ток, скользят по слою окружающей их плазмы крови.
Вязкость крови здорового человека , при патологии колеблется от , что сказывается на скорости оседания эритроцитов. Вязкость венозной крови больше, чем артериальной.
Кроме практического применения вязкости в жидкости меня удивило поведение неньютоновской жидкости.
Неньютоновская жидкость
Можно ли ходить по воде? С точки зрения физики невозможно, но это только в том случае, если речь не идет о неньютоновской жидкости. Что это за жидкость и почему по ней можно ходить, я бы хотел рассказать и объяснить в своей работе.
Ньютоновская жидкость (названная так в честь Исаака Ньютона) — вязкая, подчиняющаяся в своём течении закону вязкого трения Ньютона, жидкость. Неньютоновская жидкость — это особенная, чрезвычайно непонятная и удивительная субстанция. Загадочность такой жидкости заключается в том, что при сильном воздействии на нее, она сопротивляется словно твердое тело, в то же время, при медленном – приобретает жидкие свойства. В отличие от однородной ньютоновской, она имеет неоднородную структуру и состоит из крупных молекул. Ньютоновские и неньютоновские жидкости в последнее время вызывают активный интерес не только ученых, но и простых людей. Это связано с тем, что неньютоновская жидкость легко изготавливается своими руками и подходит для домашних опытов
В своей НИЛ я решил провести опыт с неньютоновской жидкостью, и для этого я:
смешал крахмал (250 гр.) и воду (100гр.) в глубокой тарелочке, для того чтобы увидеть удивительные свойства неньютоновской жидкости
Перемешал ингредиенты до образования однородной массы.
После этого из полученной жидкости я попытался скатать маленький шарик. Тут я заметил, что в том случае, если катать шарик очень быстро, то он будет тверже и прочнее. Если прекратить скатывать такой шарик, то он растечется по руке.
Если аккуратно опустить палец в неньютоновскую жидкость, то он без сопротивления войдет во внутрь нее, т.е. она ведет себя как жидкость; но если резко ударить кулаком по ее поверхности, то он встретит твердый отпор.
Это все объясняется тем, что частицы крахмала набухают в воде и между ними формируется физические контакты в виде хаотических сплетенных групп молекул. Эти прочные связи называются зацеплениями. При резком воздействии прочные связи не дают молекулам сдвинуться с места, и система реагирует на внешние воздействия, как упругая пружина. При медленном же воздействии молекулы успевают растянуться и распутаться, сетка рвется и молекулы равномерно расходятся. Если в опыте взять более большой объем этой жидкости и пробежаться по ней человеку, то он теоретически не утонет и продолжит движение по ней, как по твердому телу.
Итак, я могу сделать такое умозаключение, что по поверхности жидкости можно не только ходить, но и даже танцевать. Главное помнить, что неньютоновская жидкость- твердая только тогда, когда есть движение. Стоит остановиться, сразу утонешь. Итак, по жидкости ходить возможно!
Наша кровь — это тоже типичная неньютоновская жидкость. Она представляет собой суспензию эритроцитов, лейкоцитов и других элементов в плазме. А это значит, что вязкость в различных участках сосудистой системы может изменяться.
Сила жидкого трения (сила сопротивления) возникает и при движении твердого тела в жидкости. Благодаря тому, что сила сопротивления растет с увеличением скорости, любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов, начинает двигаться равномерно. Такое движение было предложено использовать для определения коэффициента вязкости.
Метод Стокса для определения коэффициента вязкости
Английским физиком и математиком Стоксом было установлено, что сила вязкого трения Fс, действующая в жидкости на движущееся тело, при небольших скоростях прямо пропорциональна скорости, т.е.
где r — коэффициент сопротивления, зависящий от размеров и формы тела, а также от вязкости среды, в которой оно движется.
Для твёрдого тела шарообразной формы радиуса R, движущегося в жидкости с коэффициентом вязкости, коэффициент сопротивления
r = 6.
Тогда по закону Стокса для модуля силы сопротивления, действующей на шарообразное тело, можно записать выражение
Fc=6
Метод Стокса позволяет определить вязкость жидкости.
На шар B массой m, объёмом V, падающий в жидкости с коэффициентом вязкости , действуют три силы: сила тяжести выталкивающая сила (сила Архимеда) и сила сопротивления (рис.1).
Сила тяжести рассчитывается по формуле
Fт= mg=V·
Рис.1
где плотность шара, g – ускорение свободного падения.
Силу Архимеда можно рассчитать, как
здесь mж – масса жидкости, вытесненной шаром, плотность этой жидкости. Сила сопротивления Fc вычисляется по формуле (22). Так как сила и постоянны, а сила возрастает с увеличением скорости движения шара, то с некоторого момента времени эти три силы могут уравновесить друг друга. Движение шара станет равномерным. В векторной форме закон движения шара запишется в виде
, или через модули сил этот закон можно записать таким образом: Fт= Fа+ Fс.
Подставив в последнее уравнение выражения для сил и получим
откуда после соответствующих преобразований получается выражение
или, учитывая, что где D- диаметр шара, последнюю формулу можно записать в виде
Практическая часть
Экспериментальное подтверждение уравнения Бернулли.
Для определения давления жидкости внутри трубки переменного сечения я решил использовать медицинские шприцы различной вместимости. Чтобы узнать давление в каждом из участков конструкции я врезал вертикально вверх трубки с небольшим диаметром, в роли которых использовал тоже шприцы. Когда жидкость протекала по моей конструкции, во врезанные трубки тоже попадала вода. И уже наглядно было видно, как изменяется давление в зависимости от диаметра трубки, по которой течет жидкость. В горизонтальном шприце с самым большим сечением столбик воды в вертикальной трубке поднимался на большую высоту, что означает – давление здесь больше. В узких местах трубы высота столбика воды меньше, чем в широких, следовательно скорость движения воды больше.
2. Определение коэффициента вязкости методом Стокса.
Приборы и принадлежности: мензурка, дробинки, микрометр, секундомер, линейка, термометр, резинки (кольцевые метки).
Цель работы: определение вязкости жидкости и характера ее изменения при увеличении температуры.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Измерить расстояние l между кольцевыми метками на цилиндре с исследуемой жидкостью (верхняя метка соответствует положению шара, при котором скорость его становится постоянной).
2. Микрометром измерить диаметры D пяти шаров (дробинок), данные занести в таблицу.
3. Для каждого шара определить время падения ti и скорость падения Vi= l/t между метками. Результаты занести в таблицу.
4. Рассчитать коэффициент вязкости жидкости по движению каждого из шаров. Для этого формулу перепишем в виде
, где к -постоянная в условиях опыта величина
Значение занести в таблицу, вычислить среднее арифметическое значение коэффициента вязкости :
Поскольку коэффициент вязкости зависит от температуры, то эксперимент по его определению проводил при различной температуре: в учебной аудитории, на холоде и в бане.
Выполнение работы.
Определение вязкости при комнатной температуре.
Определил температуру в комнате термометром. Результат t=220C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты записал в таблицу;
Далее нашел величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м3, а плотность глицерина 1260 кг/м3. В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.
Таблица результатов измерений и вычислений при t=220С
опытаDi, м
ti, с
Vi, м/c
Ŋi, 10-3Па·с
1
0,004
3
0,28
1568
2
0,004
2,96
0,29
1513
3
0,004
2,89
0,294
1493
4
0,004
3,12
0,27
1626
5
0,004
2,92
0,291
1508
Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=220С. ŋср = 1568+1513+1493+1626+1508/5= 1541 10-3Па·с
Затем я сравнил результат эксперимента со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 200С равен 1480 •10-3Па·с. Результат в ходе эксперимента мною был получен 1541• 10-3Па·с, но у меня температура была чуть больше, значит можно заявить, что коэффициенты очень близки по значению.
Определение вязкости на холоде.
Определил температуру на улице термометром. Результат t=00C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты можно увидеть в таблице;
Далее найдем величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м3, а плотность глицерина 1260 кг/м3. В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.
Таблица результатов измерений и вычислений при t=00c
опытаDi, м
ti, с
Vi, м/c
Ŋi, 10-3Па·с
1
0,004
23
0,0369
11901
2
0,004
22,92
0,037
11862
3
0,004
23,5
0,036
12195
4
0,004
22,81
0,0372
11802
5
0,004
23,2
0,0366
11996
Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=00С. ŋср = 11901+11862+12195+11802+11996/5= 11951 10-3Па·с
Затем я решил сравнить свой результат со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 00С = 12100 10-3Па·с, мой же результат равен 11951 10-3Па·с. Отсюда следует, что результаты близки по значению. Поэтому опыт проделан правильно.
Определение вязкости в бане
Определил температуру в бане термометром. Результат t=600C;
Для каждого шара определил время падения ti и скорость падения Vi между метками. Результаты можно увидеть в таблице;
Далее нашел величину k по формуле. Плотности тела и исследуемой жидкости я узнал в табличном справочнике, где плотность дроби 6300 кг/м3, а плотность глицерина 1260 кг/м3. В итоге k=2744. Затем уже рассчитал коэффициент вязкости жидкости по движению каждого из шаров также по формуле. Результаты вычислений вы также можете увидеть в таблице ниже.
Таблица результатов измерений и вычислений при t=600c
опытаDi, м
ti, с
Vi, м/c
Ŋi, 10-3Па·с
1
0,004
1,94
0,438
100
2
0,004
2,2
0,386
113
3
0,004
2
0,425
103
4
0,004
1,87
0,45
97
5
0,004
2,13
0,39
112
Также, в конце своего опыта я рассчитал среднее арифметическое значение коэффициента вязкости при t=00С. ŋср = 100+113+103+97+112/5= 105 10-3Па·с
Затем я решил сравнить свой результат со значением из табличного справочника. В справочном материале я нашел, что коэффициент вязкости глицерина при 600С = 102 10-3Па·с, мой же результат равен 105 10-3Па·с. Отсюда следует, что результаты близки по значению. Поэтому опыт проделан правильно.
Коэффициент вязкости жидкости сильно зависит от температуры помещения, где проводится опыт.
Вывод: Чем больше температура жидкости , тем меньше коэффициент ее вязкости и наоборот.
Заключение
Изучение движения жидкостей имеет важное значение для практического применения. Движение жидкости подчиняется закону (уравнению) Бернулли. Уравнение Бернулли связывает давление внутри жидкости с площадью поперечного сечения потока жидкости и скорость движения жидкости. Формула Бернулли позволяет понять, почему возникает гидродинамическая сила и позволяет измерить скорость движения жидких тел. Уравнение Бернулли позволяет понять сущность многих явлений. Например, почему есть вероятность сталкивания двух барж, кораблей, проплывающих близко друг к другу.
Течение жидкостей может быть ламинарным и турбулентным.
Если при движении существенным является трение, то вся теория гидродинамики усложняется. Поэтому при движении жидкости необходимо учитывать наличие сил внутреннего трения или вязкости. Из-за вязкости давление в жидкости уменьшается вдоль потока даже в горизонтально расположенной трубе постоянного сечения. Вязкость возникает, потому что силы взаимодействия между соприкасающимися слоями движутся с различными скоростями и переход молекул из слоя в слой связан с переносом импульса.
Сила жидкого трения (сила сопротивления) возникает и при движении твердого тела в жидкости. Благодаря тому, что сила сопротивления растет с увеличением скорости, любое тело в вязкой среде при действии на него какой-либо постоянной силы, например силы тяжести, в конце концов начинает двигаться равномерно. Это учитывается в методе Стокса для определения коэффициента вязкости жидкостей.
С помощью метода Стокса я измерил вязкость глицерина.
Вязкость жидкости зависит от ее температуры. Чем больше температура жидкости, тем меньше коэффициент ее вязкости, и наоборот.
Выполняя работу, я узнал, какие жидкости являются ньютоновскими, какие неньютоновскими.
Ньютоновские жидкости имеют широкое применение в практике и имеют немаловажное значение, неньютоновские же жидкости используются в основном ради забавы и для интересных опытов.
Знания этого раздела применяются в медицине – в лабораториях определяют вязкость крови для выяснения на содержание эритроцитов, общего содержания белка и соотношения его фракций в плазме, а также содержания в крови углекислоты. Повышение вязкости отмечается при сгущении крови и некоторых видах лейкозов (эритремии, миелофиброзах), понижение — при анемиях.
Выполняя исследовательскую работу, я понял, что выбрал именно ту тему, которая мне интересна. И выполнял ее с увлечением. Я расширил свой кругозор, и теперь могу своим сверстникам рассказать о законе сопротивления движению в вязкой жидкости Ньютона, который в школьной программе основной школы не изучается.
Я выполнил задачи, которые ставил перед собой.
Применения знаний этого раздела в различных областях современной науки и техники, биологии и медицины являются, безусловно, актуальными.
Список литературы
И.К. Кикоин «Физика – учебник для 9 класса»: Просвещение, 1990.
Г.Я. Мякишев «Физика. Механика, учебник для 10 класса» – М.: Дрофа, 2013.
Майоров А.Н. «Физика для любознательных, или о чем не узнаешь на уроке»: Академия, Ко, 1999.
Г.Е.Кирко Лабораторные работы
Т.И. Трофимова. Физика от А до Я. – 2-е изд.,-М.:Дрофа,2007.-299с.
Ф.М. Дягилев. Из истории физики и жизни ее творцов: книга для учащихся. – М.:Просвещение,1986.-255с.
Интернет — ресурсы
Жидкости с динамической вязкостью
Абсолютная или динамическая вязкость некоторых распространенных жидкостей при температуре 300 K указаны ниже:
| Жидкость | Абсолютная вязкость | |||||
|---|---|---|---|---|---|---|
| (Н · м / м 2 , Па · с ) | (сантипуаз, сП) | (10 -4 фунт / с · фут) | ||||
| Уксусная кислота | 0,001155 | 1,155 | 7.76 | |||
| Ацетон | 0,000316 | 0,316 | 2,12 | |||
| Спирт этил (этанол) | 0,001095 | 1,095 | 7,36 | |||
| Спирт метил (метанол) | 0,0006 | 3,76 | ||||
| Спирт пропил | 0,00192 | 1,92 | 12,9 | |||
| Бензол | 0,000601 | 0.601 | 4,04 | |||
| Кровь | 0,003 — 0,004 | |||||
| Бром | 0,00095 | 0,95 | 6,38 | |||
| Дисульфид углерода | 0,00036 | 0,36 | 2,428360 Углерод Тетрахлорид | 0,00091 | 0,91 | 6,11 |
| Касторовое масло | 0,650 | 650 | ||||
| Хлороформ | 0.00053 | 0,53 | 3,56 | |||
| Декан | 0,000859 | 0,859 | 5,77 | |||
| Додекан | 0,00134 | 1,374 | 9,23 | |||
| Эфир | 0,000223 | 0,000223 | ||||
| Этиленгликоль | 0,0162 | 16,2 | 109 | |||
| Трихлорфторметановый хладагент R-11 | 0.00042 | 0,42 | 2,82 | |||
| Глицерин | 0,950 | 950 | 6380 | |||
| Гептан | 0,000376 | 0,376 | 2,53 | |||
| 0,00029 0,00029 0,00029 | ||||||
| Керосин | 0,00164 | 1,64 | 11,0 | |||
| Льняное масло | 0,0331 | 33.1 | 222 | |||
| Ртуть | 0,0015 | 1,53 | 10,3 | |||
| Молоко | 0,003 | |||||
| Октан | 0,00051 | 0,51 | 3,43 | |||
| 8,0 | 54 | |||||
| Пропан | 0,00011 | 0,11 | 0,74 | |||
| Пропилен | 0.00009 | 0,09 | 0,60 | |||
| Пропиленгликоль | 0,042 | 42 | ||||
| Толуол | 0,000550 | 0,550 | 3,70 | |||
| Скипидар | 0,001375 900,24 | |||||
| Вода, пресная | 0,00089 | 0,89 | 6,0 | |||
Жидкости — температура и динамическая вязкость
- Уксусная кислота
Ацетон
Анилин
Бензол
Бромбензол
Дисульфоксид углерода
N-Бутилуглерод
Тетрахлорид углерода
Хлороформ
Диэтиловый эфир
- Этанол
Этилацетат
Этилформиат
N-гексан
n-гексадекан.
Ртуть
Метанол
Нитробензол
N-Октан
Масло касторовое
Масло оливковое
N-Пентан
N-Пропан
Серная кислота
Толуол
Вязкость, поверхностное натяжение, удельная плотность
Данная таблица предоставлена в качестве информационной службы диверсифицированных предприятий.
В этой таблице указана вязкость и поверхностное натяжение различных растворителей и других жидкостей.Аналогичный таблица, которая также включает параметры растворимости Хансена и поверхность компоненты напряжения, можно увидеть здесь . Если вас беспокоят проблемы с формулировкой, связанные с поверхностным смачивание растворимость, и вязкость control, вы можете обратиться к обеим таблицам. Каждого можно отсортировать по столбцу — просто щелкните заголовок столбца, чтобы изменить порядок эта таблица для печати.
Если есть дополнительные растворители или другие жидкости, которые, по вашему мнению, следует добавить в эту коллекцию, особенно если вы можете предоставить данные с цитатами — пожалуйста , напишите нам по электронной почте , чтобы сообщить нам об этом.
Вязкость, поверхностное натяжение, удельная плотность и молекулярный вес выбранных жидкостей
распечатать это порядок сортировки (только таблица и ссылки — откроется в новом окне браузера)
| Имя (1) | Молекулярная формула | CAS № (2) | Мол. Вес. (3) | Удельная плотность (4) | Поверхностное натяжение (5) | Вязкость (6) | |
|---|---|---|---|---|---|---|---|
| сП | CS | ||||||
| Бром | Br 2 | 7726-95-6 | 159.81 | 3,214 | 41,0 | 0,94 | 0,29 |
| Тетрахлорметан (четыреххлористый углерод) | CCl 4 | 56-23-5 | 153,82 | 1,583 | 26,3 | 0,91 | 0,57 |
| Трихлорметан (хлороформ) | CHCl 3 | 67-66-3 | 119.38 | 1,480 | 26,7 | 0,54 | 0,36 |
| Дихлорметан (хлористый метилен, DCM) | CH 2 Класс 2 | 75-09-2 | 84,93 | 1,318 | 27,8 | 0,41 | 0,31 |
| Дииодметан (йодистый метил) | CH 2 I 2 | 75-11-6 | 267.84 | 3.306 | 50,8 (7) | 2,6 (8) | 0,78 |
| Метановая кислота (муравьиная кислота) | CH 2 O 2 | 64-18-6 | 46,03 | 1,214 | 37,7 | 1,61 | 1,32 |
| Формамид (метаномид) | CH 3 NO | 75-12-7 | 45.04 | 1,129 | 57,0 | 3,34 | 2,96 |
| Нитрометан | CH 3 НЕТ 2 | 75-52-5 | 61,04 | 1,129 | 36,3 | 0,63 | 0,56 |
| Метанол (метиловый спирт) | СН 4 О | 67-56-1 | 32.04 | 0,787 | 22,1 | 0,54 | 0,69 |
| Трихлорэтилен (ТХЭ, трихлорэтилен) | С 2 HCl 3 | 79-01-6 | 131,39 | 1.458 | 28,7 | 0,55 | 0,38 |
| 1,1,1-трихлорэтан (метилхлороформ) | C 2 H 3 Класс 3 | 71-55-6 | 133.40 | 1,330 | 25,0 | 0,79 | 0,59 |
| Ацетонитрил (нитрил этана) | C 2 H 3 N | 75-05-8 | 41,05 | 0,779 | 28,7 | 0,37 | 0,47 |
| 1,2-дихлорэтан (этилендихлорид) | C 2 H 4 Класс 2 | 107-06-2 | 98.96 | 1,246 | 32,6 | 0,78 | 0,63 |
| Уксусная кислота (этановая кислота) | C 2 H 4 O 2 | 64-19-7 | 60,05 | 1.043 | 27,0 | 1,06 | 1.02 |
| Этанол (этиловый спирт) | C 2 H 6 O | 64-17-5 | 46.07 | 0,787 | 22,0 | 1,07 | 1,36 |
| Диметилсульфоксид (ДМСО) | C 2 H 6 OS | 67-68-5 | 78,13 | 1.095 | 42,9 | 1,99 | 1,82 |
| Этиленгликоль | C 2 H 6 O 2 | 107-21-1 | 62.07 | 1,111 | 48,4 | 16,1 | 14,5 |
| 2-аминоэтанол (этаноламин) | C 2 H 7 НЕТ | 141-43-5 | 61,08 | 1.014 | 48,3 | 21,1 | 20,8 |
| Акрилонитрил (этенилнитрил) | C 3 H 3 N | 107-13-1 | 53.06 | 0.801 | 26,7 | 0,34 (9) | 0,42 |
| Эпихлоргидрин (хлорметилоксиран) | C 3 H 5 ClO | 106-89-8 | 92,52 | 1,174 | 36,3 | 1,07 | 0,91 |
| Ацетон (пропанон) | C 3 H 6 O | 67-64-1 | 58.08 | 0,786 | 23,0 | 0,31 | 0,39 |
| Метилацетат | C 3 H 6 O 2 | 79-20-9 | 74,08 | 0,927 | 24,5 | 0,36 | 0,39 |
| N, N-диметилформамид (ДМФ) | C 3 H 7 НЕТ | 68-12-2 | 73.09 | 0,945 | 34,4 | 0,79 | 0,84 |
| 1-пропанол ( n -пропанол, n -пропиловый спирт) | C 3 H 8 O | 71-23-8 | 60,10 | 0.802 | 20,9 | 1,95 | 2,43 |
| 2-пропанол (изопропиловый спирт) | C 3 H 8 O | 67-63-0 | 60.10 | 0,783 | 23,3 | 2,04 | 2,61 |
| 2-метоксиэтанол (монометиловый эфир этиленгликоля) | C 3 H 8 O 2 | 109-86-4 | 76,10 | 0,960 | 42,8 | 1,7 (12) | 1,8 |
| Диметоксиметан (метилаль) | C 3 H 8 O 2 | 109-87-5 | 76.10 | 0,854 | 18,8 | 0,33 (14) | 0,39 |
| 1,2-пропандиол (пропиленгликоль) | C 3 H 8 O 2 | 57-55-6 | 76,10 | 1.033 | 45,6 | 40,4 | 39,1 |
| Глицерин | C 3 H 8 O 3 | 56-81-5 | 92.09 | 1,257 | 76,2 | 934 | 743 |
| Пропиленкарбонат | C 4 H 6 O 3 | 108-32-7 | 102,09 | 1.200 (10) | 40,9 (10) | 2,50 (10) | 2,08 |
| 2-бутанон (метилэтилкетон) | C 4 H 8 O | 78-93-3 | 72.11 | 0,799 | 24,0 | 0,41 | 0,51 |
| Тетрагидрофуран | C 4 H 8 O | 109-99-9 | 72,11 | 0,880 | 26,7 | 0,46 | 0,52 |
| 1,4-диоксан | C 4 H 8 O 2 | 123-91-1 | 88.11 | 1.029 | 32,9 | 1,18 | 1,15 |
| Этилацетат (этилэтаноат) | C 4 H 8 O 2 | 141-78-6 | 88,11 | 0,894 | 23,2 | 0,42 | 0,47 |
| Морфолин | C 4 H 9 НЕТ | 110-91-8 | 87.12 | 0,997 | 38,8 | 2,02 | 2,03 |
| 1-бутанол ( n -бутиловый спирт) | C 4 H 10 O | 71-36-3 | 74,12 | 0.806 | 25,0 | 2,54 | 3,15 |
| 2-бутанол ( сек -бутанол) | C 4 H 10 O | 78-92-2 | 74.12 | 0.805 | 22,6 | 3,10 | 3,85 |
| Диэтиловый эфир (этоксиэтан) | C 4 H 10 O | 60-29-7 | 74,12 | 0,708 | 16,7 | 0,22 | 0,31 |
| 2-метилпропиловый спирт (изобутанол) | C 4 H 10 O | 78-83-1 | 74.12 | 0,797 | 22,6 | 3,95 (15) | 4,96 |
| 1,3-бутандиол | C 4 H 10 O 2 | 107-88-0 | 90,12 | 1,002 | 47,1 | 98,3 (17) | 98,1 |
| 1,2-диметоксиэтан (DME (диметиловый эфир этиленгликоля) | C 4 H 10 O 2 | 110-71-4 | 90.12 | 0,865 | 20,0 | 1,1 (16) | 1,3 |
| 2-этоксиэтанол (моноэтиловый эфир этиленгликоля) | C 4 H 10 O 2 | 110-80-5 | 90,12 | 0,925 | 28,8 | 2,1 (11) | 2,3 |
| Диэтиленгликоль | C 4 H 10 O 3 | 111-46-6 | 106.12 | 1,114 | 55,1 | 30,2 | 27,1 |
| Диметилэтаноламин (2- (диметиламино) этанол) | C 4 H 11 НЕТ | 108-01-0 | 89,14 | 0,882 | 51,6 | 4,08 (17) | 4,63 |
| Пиридин | C 5 H 5 N | 110-86-1 | 79.10 | 0,979 | 36,7 | 0,88 | 0,90 |
| 2-фуранметанол (фурфуриловый спирт) | C 5 H 6 O 2 | 98-00-0 | 98,10 | 1,127 | 53,3 | 4,62 (17) | 4,10 |
| Метилметакрилат | C 5 H 8 O 2 | 80-62-6 | 100.12 | 0,937 | 24,2 | 0,57 (18) | 0,61 |
| N-метил-2-пирролидин | C 5 H 9 НЕТ | 872-50-4 | 99,13 | 1.025 | 44,6 | 1,67 (17) | 1,63 |
| Изопропилацетат (изопропилэтаноат) | C 5 H 10 O 2 | 108-21-4 | 102.13 | 0,871 | 22,3 | 0,52 (17) | 0.60 |
| Пропилацетат (пропилэтаноат) | C 5 H 10 O 2 | 109-60-4 | 102,13 | 0,883 | 23,9 | 0,54 | 0,61 |
| 1,2-дихлорбензол | C 6 H 4 Класс 2 | 95-50-1 | 147.00 | 1,301 | 35,7 | 1,32 | 1.01 |
| Бензол | C 6 H 6 | 71-43-2 | 78,11 | 0,873 | 28,2 | 0.60 | 0,69 |
| Анилин | C 6 H 7 N | 62-53-3 | 93,13 | 1.018 | 42,4 | 3,85 | 3,78 |
| Циклогексанон | C 6 H 10 O | 108-94-1 | 98,14 | 0,942 | 34,4 | 2,02 | 2,14 |
| Циклогексан | С 6 В 12 | 110-82-7 | 84,16 | 0.773 | 24,7 | 0,89 | 1,15 |
| Циклогексанол | C 6 H 12 O | 108-93-0 | 100,16 | 0,960 | 33,4 | 57,5 | 59,9 |
| 4-Метил-2-пентанон (метилизобутилкетон) | C 6 H 12 O | 108-10-1 | 100.16 | 0,796 | 23,5 | 0,55 | 0,69 |
| Бутилацетат | C 6 H 12 O 2 | 123-86-4 | 116,16 | 0,876 | 24,8 | 0,69 | 0,79 |
| 2-метилпропилэтаноат (изобутилацетат) | C 6 H 12 O 2 | 110-19-0 | 116.16 | 0,869 | 23,0 | 0,68 | 0,78 |
| 2-бутоксиэтанол (монобутиловый эфир этиленгликоля) | C 6 H 14 O 2 | 111-76-2 | 118,17 | 0,896 | 26,6 | 6,4 (13) | 7,1 |
| Триэтаноламин | C 6 H 15 НЕТ 3 | 102-71-6 | 149.19 | 1,120 | 51,5 | 609 | 543 |
| Бензонитрил | C 7 H 5 N | 100-47-0 | 103,12 | 1,001 | 38,8 | 1,27 | 1,27 |
| Бензальдегид | C 7 H 6 O | 100-52-7 | 106.12 | 1.040 | 38,3 | 1,4 (15) | 1,4 |
| Толуол | C 7 H 8 | 108-88-3 | 92,14 | 0,865 | 27,9 | 0,56 | 0,65 |
| Бензиловый спирт | С 7 В 8 0 | 100-51-6 | 108.14 | 1.041 | 36,8 | 5,47 | 5,25 |
| 3-метилфенол (м-крезол) | C 7 H 8 O | 108-39-4 | 108,14 | 1.030 | 35,8 | 12,9 | 12,5 |
| 2-гептанон (метил n -амилкетон) | C 7 H 14 O | 110-43-0 | 114.19 | 0,811 | 26,1 | 0,71 | 0,88 |
| n -Гептан | С 7 В 16 | 142-82-5 | 100,20 | 0,682 | 19,8 | 0,39 | 0,57 |
| Стирол (фенилэтен) | C 8 H 8 | 100-42-5 | 104.15 | 0,900 | 32,0 | 0,70 | 0,78 |
| Ацетофенон (1-фенилэтанон) | C 8 H 8 O | 98-86-2 | 120,15 | 1.024 | 39,0 | 1,68 | 1,64 |
| Этилбензол | С 8 В 10 | 100-41-4 | 106.17 | 0,865 | 28,6 | 0,63 | 0,73 |
| o -Ксилол | С 8 В 10 | 95-47-6 | 106,17 | 0,876 | 29,6 | 0,76 | 0,87 |
| p -ксилол | С 8 В 10 | 106-42-3 | 106.17 | 0,861 | 27,9 | 0.60 | 0,70 |
| Феноксиэтанол (монофениловый эфир этиленгликоля) | C 8 H 10 O 2 | 122-99-6 | 138,16 | 1,11 (17) | – | 20,3 (17) | 18,3 |
| Октановая кислота (каприловая кислота) | C 8 H 16 O 2 | 124-07-2 | 144.21 | 0,903 | 27,9 | 5,02 | 5,56 |
| 2-этил-1-гексанол | C 8 H 18 O | 104-76-7 | 130,23 | 0,830 | 27,7 | 6,27 | 7,55 |
| Изофорон | C 9 H 14 O | 78-59-1 | 138.21 | 0,920 | 35,5 | 2,33 | 2,53 |
| 1-бромнафталин | C 10 H 7 Br | 90-11-9 | 207.07 | 1.478 | 44,4 | – | – |
| Дибутилфталат | C 16 H 22 O 4 | 84-74-2 | 278.34 | 1.043 | 37,4 | 16,6 | 15,9 |
| гексадекан | С 16 В 34 | 544-76-3 | 226,44 | 0,770 | 27,1 | – | – |
| Диоктилгександиоат (диоктиладипат) | C 22 H 42 O 4 | 103-23-1 | 370.57 | 0,92 (19) | – | 13,7 (19) | 14,9 |
| Бис (2-этилгексил) фталат (BEHP, диоктилфталат) | C 24 H 38 O 4 | 117-84-0 | 390,56 | 0,980 | 31,1 | 80 (20) | 82 |
| Вода | H 2 O | 7732-18-5 | 18.02 | 0,999 | 72,7 | 0,89 | 0,89 |
| Перекись водорода | H 2 O 2 | 7722-84-1 | 34,02 | 1.449 | 74,0 | 1,25 (15) | 0,86 |
| Гидразин | H 4 N 2 | 302-01-2 | 32.04 | 0,950 | 66,9 | 0,88 | 0,93 |
| Меркурий | рт. Ст. | 7439-97-6 | 200,59 | 13,630 | 474,4 | 1,53 | 0,11 |
| Тетрахлорид кремния | SiCl 4 | 10026-04-7 | 169,90 | 1.645 | 18,8 | 99,4 | 60,4 |
(1) Выбор номенклатуры — один из самых сложных задачи по составлению любой таблицы химических данных, особенно содержащей различные углеводороды, которые стали широко известны ненаучным имена. Обычно мы использовали IUPAC (Международный союз чистых и прикладных Химия) номенклатура в качестве основного наименования; широко используемые синонимы также включены — иногда они отображаются как основное имя, в зависимости от по обычному использованию.В очень редких случаях обозначение ИЮПАК носит технический характер, и не получили широкого распространения в промышленности, поэтому не были включены в эту таблицу. полностью. Всегда лучше ссылаться на CAS (Chemical Abstracts Service). числа, чтобы убедиться, что оценивается правильный материал.
(2) Теплофизические свойства химических веществ и углеводородов , Карл Л. Яу, Уильям Эндрю, Норвич, Нью-Йорк, 2008, если не указано иное.
(3) Регистрационный номер службы химических рефератов: Справочник CRC по химии и физике, 85-е издание , Дэвид Р.Lide, ed., CRC Press, Boca Raton, FL, 2004, если не указано иное.
(4) г / мл при 25 o C (298,15 K): Теплофизические свойства отдела химикатов и углеводородов , Карл Л. Яу, Уильям Эндрю, Норвич, NY, 2008, если не указано иное.
(5) дин / см при 25 o C (298,15 K): Теплофизический Свойства химикатов и углеводородов , Карл Л. Яу, Уильям Эндрю, Норвич, штат Нью-Йорк, 2008 г., если не указано иное.
(6) Вязкость при 25 o C (298,15 K): Справочник CRC of Chemistry and Physics, 85th Edition , David R. Lide, ed., CRC Press, Бока-Ратон, Флорида, 2004 г., если не указано иное. cP — это аббревиатура от сантипуаз, стандартная единица измерения вязкости. cs — это сокращение для сантистока, который является мерой, используемой в чашечных испытаниях на вязкость; это равно сантипуаз, деленный на удельную плотность.
(7) http: // www.surface-tension.de/LIQUIDS составляет 50,9 дин / см @ 20 o C (293,15 К).
(8) @ 25 o C: http://www.heavyliquids.com/product_LST/org.htm.
(9) @ 25 o C: Химия акрилонитрила , American Cyanamid Co., 1951, стр. 11-19.
(10) @ 25 o C: http://www.huntsman.com/performance_products/Media/JEFFSOL_Alkylene_Carbonates_(brochure).pdf.
(11) @ 20 o C: http://www.advancepetro.com/egmee.htm.
(12) @ 20 o C: http://www.advancepetro.com/egmme.htm.
(13) @ 20 o C: http://www.advancepetro.com/egmbe.htm.
(14) @ 30 o C: http://www.lcy.com.tw/msds/en/LCY020E.pdf.
(15) @ 20 o C: http://www.wikipedia.org/wiki.
(16) @ 20 o C: http://www.alibaba.com/product-gs/209
(17) @ 20 o C: http://solvdb.ncms.org/common01.idc.
(18) @ 25 o C: http://www.methylmethacrylate.eu.
(19) @ 20 o C: https://fscimage.fishersci.com/msds/54816.htm.
(20) @ 20 o C: http: // www.alibaba.com/product-free/11745259/Dioctyl_Phthalate_Dop_.html.
InnoCal Solutions — Таблица значений вязкости
См. Значения вязкости 16 распространенных жидкостей
Прочтите таблицу значений.
Запросить ценовое предложение
Значения вязкости| сантипуаз * (сП) | Сантистоксов (сСт) | Saybolt Second Универсальный (SSU) | Типичная жидкость |
| 1 | 1 | 31 | Вода |
| 3.2 | 4 | 40 | Молоко |
| 12,6 | 15,7 | 80 | Мазут № 4 |
| 16,5 | 20,6 | 100 | Крем |
| 34,6 | 43,2 | 200 | Масло растительное |
| 88 | 110 | 500 | SAE 10 масло |
| 176 | 220 | 1000 | Томатный сок |
| 352 | 440 | 2000 | Масло SAE 30 |
| 880 | 1100 | 5000 | Глицерин |
| 1561 | 1735 | 8000 | Масло SAE 50 |
| 1760 | 2200 | 10 000 | Мед |
| 3000 | 4500 | 20 000 | Клей |
| 5000 | 6250 | 28 000 | Майонез |
| 8640 | 10 800 | 50 000 | Меласса B |
| 15 200 | 19 000 | 86 000 | Сметана |
| 17,640 | 19 600 | 90 000 | Масло SAE 70 |
Запросить ценовое предложение
Вязкость жидкости — обзор
8.2.2 Неньютоновские жидкости
Было показано, что существует простая взаимосвязь между ньютоновскими и многими неньютоновскими данными энергопотребления в ламинарном режиме с использованием корреляции Метцнера и Отто 8 , основанной на расчетах кажущейся вязкости для смесителей. В основе метода лежит предположение, что существует средняя скорость сдвига для смесителя, которая описывает потребляемую мощность, и что эта скорость сдвига прямо пропорциональна скорости вращения рабочего колеса:
(8,10) γA = KsN
, где k с — постоянная скорости сдвига смесителя.Средняя скорость сдвига γ˙ A определяет кажущуюся вязкость для прогнозирования мощности неньютоновских жидкостей. Кажущаяся вязкость определяется по вискозиметрическим данным при соответствующей скорости сдвига и используется непосредственно в обычном ньютоновском силовом числе — корреляции числа Рейнольдса (силовая кривая). Чтобы проверить эту гипотезу, производятся измерения числа мощности — характеристик числа Рейнольдса для ньютоновских жидкостей и числа мощности — характеристик скорости рабочего колеса для неньютоновских жидкостей. Для измеренного значения потребляемой мощности для неньютоновской жидкости число мощности и соответствующее число Рейнольдса можно рассчитать по кривой ньютоновской мощности.Затем, используя определение числа Рейнольдса для неньютоновской жидкости, например:
(8,11) Re = ND2pμa
μ , можно определить . Скорость сдвига, соответствующая этой кажущейся вязкости, может быть определена из данных кажущейся вязкости — скорости сдвига неньютоновской испытательной жидкости, см. , рис. 8.4, . Константа скорости сдвига смесителя, k s , затем может быть определена из уравнения (8.10). Значения k s , определенные Метцнером и Отто 8 , были относительно постоянными для диапазона скоростей рабочего колеса и свойств жидкости, и среднее значение можно было использовать для прогнозирования неньютоновских данных о потреблении энергии.Использование средней скорости сдвига и кажущейся вязкости также показывает потенциал для прогнозирования потребления энергии для тиксотропных жидкостей. 9
Рисунок 8.4. Определение скорости сдвига (k s ) по экспериментальным данным, (а) неньютоновская потребляемая мощность; (б) Ньютоновское энергопотребление; (c) неньютоновская вискозиметрия
Для жидкостей по степенному закону k s может быть включено в уравнение степенного числа — числа Рейнольдса. Для жидкости со степенным законом:
(8.12) τ = K (γ˙A) n
и кажущаяся вязкость:
(8,13) μa = τγ˙A = K (γ˙A) n − 1
Если γ˙A = k с N , тогда:
(8.14) μa = K (ksN) n − 1
Это значение μ a может быть включено в число Рейнольдса:
(8.15) Re = ND2ρμa = N2 − nD2ρK (ks ) n − 1
Уравнение числа мощности (8.5) для ламинарного потока может быть переписано как:
(8.16) Po = KP [N2 − nD2pK (ks) n − 1] −1
, где значение K p действительно для ньютоновских и неньютоновских жидкостей.Важно отметить наличие константы скорости сдвига смесителя в уравнении числа мощности, и корреляции, которые не включают эту константу или какой-либо эквивалент, должны быть тщательно проверены перед применением.
Простая концепция средней скорости сдвига смесителя широко использовалась в лабораторных и промышленных работах, и в большинстве случаев предполагалось, что константа скорости сдвига, k s , зависит только от типа рабочего колеса. Продолжаются исследования возможного влияния 10 показателя текучести и упругих свойств, а также процедур, необходимых для описания потребляемой мощности для жидкостей дилатанта 11 .Следует отметить, что во всех аспектах прогнозирования мощности и анализа данных модели степенного закона (уравнение 8.12) следует использовать только с осторожностью. Кажущаяся изменчивость k s может быть связана с неправильным использованием уравнений степенного закона; при проведении расчетов следует убедиться, что средние представляющие интерес скорости сдвига (γ˙ A = k s N ) лежат в пределах диапазона степенных вискозиметрических данных.
Предполагается и, по-видимому, успешно, что константа скорости сдвига, k s , не зависит от размера оборудования (нет проблем с масштабированием) и небольших отклонений в геометрии оборудования.
Для рабочих колес, диаметр которых меньше диаметра резервуара, были измерены следующие константы скорости сдвига, k s
Турбинные двигатели с 6 лопастями = 11,52 лопастных лопастных двигателя ks = 103 лопастных гребных винта = 10
Для спиральных лент и анкеров зазор стенки сильно влияет на константу скорости сдвига:
(8,17) для лент Ks = 34−114 (CD) для 0,026 (8,18) для анкеров ks = 33−172 ( CT) для 0.02 Приведенные выше константы скорости сдвига получены на основе измерений мощности, выполненных в ламинарном режиме. Они не действуют строго для переходного и турбулентного течения. Однако в турбулентной области рассеяние мощности определяется инерционными эффектами и не зависит от вязкости. Таким образом, нет необходимости оценивать среднюю скорость сдвига в турбулентном потоке для прогнозирования кажущейся вязкости и, следовательно, потребляемой мощности, см. Уравнение (8.9). Скорости сдвига и напряжения, относящиеся к турбулентному потоку, обсуждаются далее в этой главе. Некоторое типичное потребление энергии для резервуаров с мешалкой приведено ниже 12 , что дает приблизительное представление о величине потребляемой мощности для определенных задач. Эти значения предназначены только для использования в качестве практических значений и не исключают необходимости выполнять правильные расчеты размеров с использованием соответствующих кривых мощности. Следует иметь в виду, что потребляемая мощность, рассчитываемая по кривым мощности, дает меру энергии, рассеиваемой в жидкости. Он не указывает на то, эффективно ли рассеивается эта мощность.Кроме того, он не содержит потерь, которые возникают в двигателе / редукторе / подшипниках, которые необходимо учитывать при выборе привода. Стоит отметить, что расчет требуемой мощности требует знания скорости крыльчатки, и именно это значение трудно определить, например: Какая скорость крыльчатки необходима для смешивания содержимого танка в заданное время? Какая скорость рабочего колеса потребуется для достижения желаемой скорости массообмена при контакте газа и жидкости? Ответы на подобные вопросы требуют подробного рассмотрения механизмов перемешивания / массопереноса, и они рассматриваются в следующих главах.В настоящей главе мы разработали метод расчета потребляемой мощности в однофазной системе, если известна скорость рабочего колеса. Можно распространить описанную выше процедуру на определенные многофазные приложения, в которых необходимо оценить потребляемую мощность. В случае систем жидкость / жидкость с низкой вязкостью, которые встречаются при экстракции растворителем, и для крупных твердых частиц, взвешенных в жидкостях с низкой вязкостью при низких концентрациях, операция, вероятно, будет проводиться в турбулентной области.В таких случаях можно использовать кривые однофазной мощности, при этом средняя плотность используется как для числа мощности, так и для числа Рейнольдса. Однако такой подход не должен использоваться для систем газ / жидкость, где прогнозы, основанные на средних значениях плотности, могут привести к значительному завышению требований к мощности. Это подробно рассматривается в главе 15. Наконец, для систем жидкость / жидкость, которые образуют стабильные эмульсии, и для систем твердое / жидкое с высокими концентрациями, вероятно, будут встречаться неньютоновские свойства.В таких случаях следует использовать уравнения 8.10–8.18. Абсолютная вязкость многих жидкостей относительно не изменяется с давлением, но очень чувствительна к температуре. Для изотермического течения вязкость во многих случаях можно считать постоянной. Изменения температуры воздуха и воды в зависимости от температуры при атмосферном давлении показаны на рисунках 1.8 и 1.9. Некоторые распространенные материалы (чистые и смешанные) имеют выражения, дающие оценку.\ frac {3} {2} \] Где \ (\ mu \) вязкость при температуре на входе, Т \ (\ mu_ {0} \) эталонная вязкость при эталонной температуре, \ (T_ {i0}) \ (T_ {in} \) температура на входе в градусах Кельвина \ (T_ {i0} \) эталонная температура в градусах Кельвина \ (Suth \) Константа Сазерленда (представлена в таблице 1.1) Пример 1.3 Рассчитайте вязкость воздуха при 800K на основе уравнения Сазерленда. Используйте данные, приведенные в таблице 1.2} \ right] \) Низкая мощность суспендирование легких твердых частиц, смешивание жидкостей с низкой вязкостью 0,2 кВт / м 3 Средняя мощность небольшая теплопередача, диспергирование газа, контакт жидкость / жидкость, суспендирование средней плотности твердые тела 0.6 кВт / м 3 Высокая мощность суспендирование тяжелых твердых частиц, эмульгирование, диспергирование газа 2 кВт / м 3 Очень высокая мощность замеса пасты, теста 4 кВт / m 3 1.5.4: Оценка вязкости
Таблица 1.2} \ right] \)
Рис. 1.10. Вязкость жидких металлов как функция температуры.
Жидкие металлы
Жидкий металл можно рассматривать как ньютоновскую жидкость для многих приложений. Кроме того, многие алюминиевые сплавы ведут себя как ньютоновская жидкость до тех пор, пока не появится первое затвердевание (при условии термодинамических свойств в установившемся состоянии).Даже при затвердевании (мягкая зона) поведение металла можно оценить как ньютоновский материал (дальнейшее чтение можно сделать в книге этого автора « Основы проектирования литья под давлением »). На рис. 1.10 показаны несколько жидких металлов (из The Reactor Handbook, Vol. Atomic Energy Commission, AECD-3646, Типография правительства США, Вашингтон, округ Колумбия, май 1995 г., стр. 258.)
Общие графики вязкости
В случае « обычных » жидкостей, для которых информация ограничена, Хоуген и др. Предложили использовать график, аналогичный графику сжимаемости.На этом графике, если одна точка хорошо задокументирована, можно оценить другие точки. Кроме того, этот график также показывает тенденции. На рисунке 1.11 относительная вязкость \ (\ mu_ {r} = \ mu / \ mu_ {c} \) представлена как функция относительной температуры \ (T_ {r} \). \ (\ mu_ {c} \) — вязкость в критическом состоянии, а \ (\ mu \) — вязкость в любом заданном состоянии. Проведены линии постоянного относительного давления \ (P_ {r} = P / P_ {c} \). Для практических целей нижнее давление составляет \ (\ sim1 [бар] \).
Таблица 1.2} \ right] \)
Критическое давление можно оценить тремя способами.2] \]
Рис. 1.11. Пониженная вязкость как функция пониженной температуры.
Рис. 1.12. Пониженная вязкость как функция пониженной температуры.
Вязкость смесей
В общем, вязкость жидкой смеси должна оцениваться экспериментально. Даже для однородной смеси нет серебряной пули для оценки вязкости. В этой книге для аналитического выражения обсуждается только смесь газов с низкой плотностью.2 \)
Здесь,
\ (n \) количество химических компонентов в смеси
\ (x_ {i} \) — мольная доля компонента \ (i \)
\ mu_ {i} вязкость компонента \ (i \)
Нижний индекс \ (i \) следует использовать для индекса \ (j \).
Безразмерный параметр \ (\ phi_ {ij} \)
равно единице, когда \ (i = j \). Вязкость смеси сильно нелинейно зависит от долей компонентов.
Пример 1.{\ circ} C \).
Решение 1.5
В следующей таблице приведены известные подробности
Сводная таблица 1.
| Компонент | Молекулярный вес, \ (M \) | Дробь, \ (x \) | Вязкость, \ (\ mu \) |
| \ (О_2 \) | 32. | 0,2 | 0,0000203 |
| \ (Н_2 \) | 28. | 0,8 | 0.00001754 |
Сводка таблицы 2.
| i | j | \ (М_и / М_j \) | \ (\ mu_i / \ mu_j \) | \ (\ Phi_ {ij} \) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1,0 | 1,0 | 1,0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 1,143 | 1,157 | 1,0024 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 1 | 0.2} \ right] \). Теоретически при очень низком давлении вязкость зависит только от температуры с « простой » молекулярной структурой. Для газов с очень длинной молекулярной структурой или сложной структурой эти формулы неприменимы. Для некоторых смесей двух жидкостей было замечено, что при низком напряжении сдвига в вязкости преобладает жидкость с высокой вязкостью, а при высоком напряжении сдвига преобладает жидкость с жидкостью с низкой вязкостью. Более высокая вязкость преобладает при низком напряжении сдвига.{n} \, x_i \, {\ mu_c} _i \] Пример 1.6 Рис. 1.13 Концентрирующие цилиндры с вращающимся внутренним цилиндром. с радиусом 0,101 [м] и длиной цилиндров 0,2 [м]. Принято, что момент 1 [\ (N \ times m \)] необходим для поддержания угловой скорости 31,4 оборота в секунду (эти числа представляют собой только академический вопрос, а не реальную ценность реальной жидкости). Оцените вязкость жидкости, используемой между цилиндрами.} Решение 1.6 Момент или крутящий момент передается через жидкость на внешний цилиндр. Контрольный объем вокруг внутреннего цилиндра показывает, что момент является функцией площади и напряжения сдвига. Расчет напряжения сдвига можно оценить как линейный между двумя концентрическими цилиндрами. Скорость на внутренней поверхности цилиндров равна \ [\ label {концентрические цилиндры: Ui} U_i = r \, \ omega = 0,1 \ times 31,4 [рад / секунда] = 3,14 [м / с] \] Скорость на внешней поверхности цилиндра равно нулю. Градиент скорости можно считать линейным, следовательно, \ [\ label {concylinders: dUdr} \ dfrac {dU} {dr} \ cong \ dfrac {0.{\ circ}} {3} \] Пример 1.8 Рис. 1.14 Вращающийся диск в установившемся режиме. Краевыми эффектами можно пренебречь. Указанный зазор равен \ (\ delta \), а скорость вращения равна \ (\ omega \). Напряжение сдвига можно считать линейным.} Решение 1.8 В этом случае напряжение сдвига является функцией радиуса \ (r \), и необходимо разработать выражение. Кроме того, дифференциальная площадь также увеличивается и является функцией \ (r \).4} {2 \, \ delta} \] Авторы и авторство
Вязкость и удельный вес — Продукция Force EngineeredВязкость — Свойство жидкости, которая сопротивляется любой силе, способствующей течению. Это свидетельство сцепления между частицами жидкости, которое заставляет жидкость оказывать сопротивление, аналогичное трению.Повышение температуры обычно снижает вязкость; наоборот, снижение температуры обычно увеличивает вязкость. Потери на трение в трубе увеличиваются с увеличением вязкости. Удельный вес — Прямое отношение веса любой жидкости к весу воды при 62 градусах F. Вода при 62 градусах F весит 8,33 фунта на галлон и обозначается как 1,0 sp. гр. Удельный вес жидкости не влияет на характеристику центробежного насоса. Он просто влияет на мощность, необходимую для вращения насоса с необходимой скоростью.Поправка на требования к HP для жидкостей с удельным весом, отличным от 1,0, рассчитывается с использованием .
Таблица преобразования вязкостиВлияние вязкости — Вязкие жидкости имеют тенденцию увеличивать HP насоса, снижать эффективность, уменьшать производительность и напор и увеличивать трение в трубе.
* Пуасы и сантипуазы даны для масла.8 спец. Отношение: сантистоксы x удельный вес = сантипуазТаблицы удельного веса
* На основе веса одного галлона воды при 60 ° F в воздухе 3,328 фунта.
Приблизительная вязкость и удельный вес обычных жидкостей
* Приведенные значения являются средними значениями, фактическая вязкость может быть больше или меньше указанного значения. Справочные значения и справочные корреляции для теплопроводности и вязкости жидкостей2.1. ТеплопроводностьТеплопроводность жидкости λ оказалась одним из самых сложных теплофизических свойств для точного измерения. Важно помнить, что теплопроводность, λ ( T , P ), является зависящей от состояния константой пропорциональности в законе Фурье, связывающем тепловой поток с бесконечно малым градиентом температуры.Только в 1951 г. было сделано какое-либо предложение относительно стандартных эталонных значений для этого свойства жидкости. В то время Riedel 1 предложил принять теплопроводность жидкого толуола (жидкости, которая может быть легко получена с высокой степенью чистоты) в качестве эталонного значения при 293,15 К и 0,1 МПа. Сложность, присущая измерению теплопроводности как жидкостей, так и газов, возникает из-за невозможности разделить процессы, связанные с переносом тепла: теплопроводность, конвекцию и излучение.Отсутствие гравитационного поля (например, космические измерения) может смягчить конвективный тепловой поток, а лучистый тепловой поток обычно не представляет проблемы при низких температурах. В 1986 году, в связи с быстрым развитием измерения теплопроводности, в первую очередь жидкостей в жидкой фазе, Ньето де Кастро и др. . 2 предложил полную переоценку исходных значений теплопроводности. Работа проводилась под эгидой Подкомитета по транспортным свойствам (с 2001 года известного как Международная ассоциация транспортных свойств, IATP) Международного союза теоретической и прикладной химии, IUPAC. Переоценка проводилась в форме критического анализа экспериментальных измерений теплопроводности ряда важных жидкостей, что позволило характеризовать имеющиеся данные как первичные или вторичные в соответствии с их оценочной неопределенностью. Следующие рекомендации использовались как средство идентификации первичных данных: 2
Используются только первичные данные, когда это необходимо, для определения эталонной корреляции или для разработки рекомендуемых эталонных значений. Эти рекомендации по оценке литературных данных о транспортных свойствах продолжали служить руководством для дальнейшей работы IATP как по справочным данным, так и по корреляциям. 2.1.1. Эталонные значения теплопроводности жидкостейТолуол и вода были предложены в качестве эталонных жидкостей по теплопроводности. Ньето де Кастро и др. . 2 рекомендовал в 1986 году следующие справочные значения, которые действуют и сегодня: для толуола при 298,15 К и 0,1 МПа, λ = 0,1311 ± 0,0026 Вт · м − 1 · K − 1. (1) а для воды при 298,15 К и 0,1 МПа λ = 0,6067 ± 0.0122 Вт · м − 1 · K − 1. (2) Об этих расширенных неопределенностях сообщалось с доверительной вероятностью 95%. Температурная зависимость теплопроводности жидкого толуола при 0,1 МПа была представлена 2 следующими уравнениями, действующими и сегодня, где T * = (T / 298,15 K) и λ * = (λ (T) / λ (298,15 K)): диапазон температур 230 K ≤ T ≤ 360 K, λ * = 1,68182 — 0,682022 T * (3) , и расширенный диапазон 189 K ≤ T ≤ 360 K, λ * = 1.45210 — 0,224229 T * — 0,225873 T * 2 (4) . Учитывая неопределенность первичных экспериментальных данных, относительная расширенная неопределенность теплопроводности по формуле. (3) составляет 2,2% и из уравнения. (4) составляет 2,6% при уровне достоверности 95%. В случае воды рекомендация IAPWS 2012 г. 4 предложила следующее уравнение как функцию температуры, действительное при 0,1 МПа, в диапазоне температур 273,15 K ≤ T ≤ 383.15 К, так как λ (T) / 1 мВт м − 1K − 1 = 1,663Tr − 1,15−1,7781Tr − 3,4 + 1,1567Tr − 6−0,432115Tr − 7,6 (5) где T r = T / (300 K). Коэффициент теплопроводности с расширенной относительной неопределенностью из этого уравнения составил 1,5% при уровне достоверности 95%. Другие эталонные значения теплопроводности жидкости и ограниченные корреляции имеют немного большую погрешность, например n -гептан, 2 и бензол. 5 2.1.2. Справочные значения теплопроводности газовЗа последние два десятилетия был достигнут значительный прогресс в установлении справочных значений теплопроводности благородных газов при низких плотностях. Это в основном результат теоретических достижений в ab-initio определении поверхностей потенциальной энергии межмолекулярных пар для благородных газов, что стало возможным благодаря быстрому увеличению вычислительной мощности. Cencek и др. . 6 разработал наиболее точную на сегодняшний день поверхность потенциальной энергии пар и использовал ее для расчета термофизических свойств гелия в состоянии разбавленного газа в диапазоне температур от (1 до 104) K с погрешностями почти на два порядка меньше. чем у самых точных измерений. Расчеты Cencek и др. . 6 приводят к следующему эталонному значению теплопроводности гелия при 25 ° C, 0,1 МПа, λ He = 0.155 000 8 ± 0,000 001 5 Wm −1 K −1 . Май и др. . 7, 8 показали, что для благородных газов отношение теплопроводности к вязкости может быть очень точно рассчитано с использованием современной парной потенциальной функции ab-initio с классической кинетической теорией. Таким образом, комбинируя эталонные экспериментальные отношения вязкости с точными ( λ / η ) отношениями, рассчитанными с использованием потенциалов Hellmann и соавторов, 9–12 , ab-initio свойства гелия могут быть использованы для определения рекомендуемых значений для теплопроводность неона, аргона, криптона и ксенона при 25 ° C, 0.1 МПа, который мы представляем. Границы ошибки соответствуют расширенной ( k = 2) неопределенности с доверительным интервалом 95%. ТАБЛИЦА 1.Контрольные значения теплопроводности выбранных газов при 25 ° C и 0,1 МПа основаны на экспериментальных соотношениях вязкости с точными ( λ / η ) соотношениями.
Свойства переноса разбавленного газа, оцененные из abinitio парные потенциальные функции строго оцениваются в пределах нулевой плотности.Для сравнения с экспериментом значения, полученные из теории, должны быть скорректированы, чтобы соответствовать давлению, при котором проводилось измерение, с использованием начальной зависимости этого транспортного свойства от плотности. Эта начальная зависимость плотности зависит от температуры и может быть оценена с помощью теории соответствующих состояний Rainwater-Friend; 13 такими поправками можно пренебречь при 0,1 МПа для гелия при 25 ° C. Значения λ Ne , λ Ar , λ Kr и λ Xe при 25 ° C, перечисленные в, уже применяли эту корректировку с использованием начальной зависимости плотности от Bich. и др. ., 9 , что составляет примерно 0,04%, 0,23%, 0,41% и 0,71% соответственно. Примечательно, что современные справочные значения для благородных газов при 25 ° C и 0,1 МПа, перечисленные выше, отличаются от значений теплопроводности благородных газов (), рекомендованных Кестином и др. . 14 в 1980 году менее чем на 0,42%. Это по существу находится в пределах расширенной относительной неопределенности, оцененной Кестином и др. . 14 (0,6% в диапазоне 25–200 ° C и 1% в диапазоне 200–500 ° C при уровне достоверности 95%).Мы рекомендуем использовать значения, представленные выше, для теплопроводности газов при 298,15 К и 0,1 МПа. При более высоких температурах его можно использовать напрямую для получения теплопроводности газа. ТАБЛИЦА 2.Значения, рекомендованные Кестином и др. . № 14 в 1980 г. для теплопроводности благородных газов при 0,1 МПа. Они согласуются с современными эталонными значениями, привязанными к свойствам гелия, рассчитанным ab initio на уровне неопределенности, оцененном Кестином и др. . 14
Для более высоких давлений, до 30 МПа и температуры 27,5 ° C, теплопроводность газообразного аргона представлена уравнением 14 (с поправкой на текущее действующее уравнение состояния аргона 15 ) λ = 17,743 + 21,440 × 10−3ρ + 28,321 × 10−6ρ2 (6) где λ измеряется в мВт · м −1 K −1 и ρ в кг · м -3 . Широкий диапазон эталонных корреляций для этих газов даст немного разные значения при оценке в фиксированных точках этих эталонных значений. При 25 ° C и 0,1 МПа корреляции в базе данных 16 NIST REFPROP версии 10 дают (0,15531 и 0,017745) Вт м −1 K −1 для гелия 17 и аргона 18 соответственно. По сравнению с, мы отмечаем разницу в 0,2% и 0,4% соответственно для этих благородных газов. Хотя эти сравнения указывают на взаимное согласие в пределах заявленных неопределенностей, они служат для повторного подчеркивания нескольких моментов.Контрольные значения часто более точны, чем контрольные корреляции, и контрольные значения предпочтительнее для калибровок, когда их достаточно. Даты и источники, связанные с конкретным эталонным значением и эталонной корреляцией, являются важными факторами при выборе лучшего источника для приложения. 2.2. ВязкостьВ этой работе мы рассматриваем только динамическую ньютоновскую вязкость — коэффициент линейного отклика на бесконечно малую скорость сдвига. 2.2.1. Контрольные значения вязкости жидкостейВязкость воды является одним из наиболее важных стандартов вискозиметрии, и Международная ассоциация свойств воды и пара (IAPWS) поддерживает текущие международные консенсусные стандарты для жидкости. В соответствии с эталонной корреляцией IAPWS, ISO / TR 3666: 199819 предоставляет международно согласованное стандартное значение вязкости жидкой воды при 20 ° C и атмосферном давлении (0,101 325 МПа): согласованное эталонное значение составляет Это значение имеет расширенную относительную неопределенность, равную 0.17% (при доверительной вероятности 95%). Эталонное значение в значительной степени основано на экспериментальном значении 1,0019 мПа с, сообщенном Swindells et al . 20 в 1952 году, что также было основой ISO / TR 3666: 1977. Стандартное значение, приведенное в уравнении (7), объясняет разницу между температурными шкалами ITS-48 и ITS-90. Справочное уравнение 2009 IAPWS 21 для жидкой воды при 0,1 МПа от 253,15 К до 383,15 К η / 1 мкПа · с = 280,68Tr − 1,9 + 511.45Tr − 7,7 + 61.131Tr − 19,6 + 0,45903Tr − 40,0 (8) с T r = T / (300 K). Расширенная относительная неопределенность этого уравнения составляет 1,5% при уровне достоверности 95%. Эта эталонная корреляция дает значение 1,0016 мПа с при 20 ° C и 0,1 МПа, что соответствует стандартному эталонному значению ISO / TR 3666: 199819. В недавней статье 22 была предложена эталонная корреляция для толуола. В конкретном диапазоне от 263 до 273 К и 0.1 МПа предложенные значения вязкости имели погрешность 0,7% (при уровне достоверности 95%). Следующее уравнение соответствует этим значениям с погрешностью менее 0,1%. η / 1 мкПа · с = 47,53−304,968Tr + 75,285Tr2 — 838,095Tr3 + 353,120Tr4 (9) где в данном случае T r = T / T c и T c — критическая температура толуола 22 (= 591,75 K). 2.2.2. Эталонные значения вязкости газовВ случае вязкости газов теоретические достижения, обсуждаемые в разделе 2.1.2, позволяют рассчитывать теплофизические свойства гелия при низких плотностях и приводят к наиболее точно известному стандарту вязкости с относительной неопределенность около 10 −5 при температуре окружающей среды. 6 Путем объединения контрольных значений отношений вязкости, полученных из измерений, с исходной вязкостью гелия, вязкости H 2 , CH 4 , Ne, N 2 , C 2 H 6 , Ar, C 3 H 8 , Kr, Xe и SF 6 также можно определить при 25 ° C и 0.1 МПа (с использованием начальных зависимостей плотности, представленных Berg и Moldover 23 ) и перечислены в. Таблица 3.Эталонные значения вязкости 11 газов при 25 ° C и 0,1 МПа 23 и их расширенная неопределенность при уровне достоверности 95%, U ( η ).
Эталонные значения вязкости благородных газов при давлении 0,1 МПа и температурах до 500 ° C, рекомендованные Wakeham et al . 24 показаны в.Эти значения отличаются от значений вязкости, перечисленных для благородных газов при 25 ° C и 0,1 МПа, менее чем на 0,33%, что в основном согласуется с оценками неопределенности, представленными Wakeham et al . 24 (0,2% в диапазоне 25-200 ° C и 0,4% в диапазоне 200-500 ° C). В принципе, неопределенность этих значений может быть уменьшена в несколько раз путем объединения контрольных значений, перечисленных в, с отношением вязкости газа при температуре T к вязкости при 25 ° C, рассчитанной с использованием парного потенциала abinitio , 9 , 10 вместе с небольшой поправкой на начальную зависимость плотности из Bich et al . 11 ТАБЛИЦА 4.Справочные значения вязкости благородных газов при 0,1 МПа. 24
Наконец, отметим, что программа NIST REFPROP 16 , обсуждаемая в следующем разделе, использует множество индивидуальных широких корреляций от разных авторов, разработанных в разное время для расчета значений вязкости и не обязательно воспроизводит рекомендуемые значения с точностью до указанной неопределенности в. Для калибровки прибора значения в предпочтительнее значений, найденных в корреляциях в REFPROP 16 , и всегда следует проверять, есть ли новые рекомендации. Вязкость газа при несколько более высоких давлениях с погрешностями, сравнимыми с погрешностями, достигаемыми в настоящее время при 0,1 МПа, в принципе, может быть получена с использованием адаптации метода двухкапиллярного вискозиметра, как описано Berg et al . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Н. БОБЫЛЁВ «ФИЗИЧЕСКИЕ СВОЙСТВА НАИБОЛЕЕ ИЗВЕСТНЫХ ХИМИЧЕСКИХ ВЕЩЕСТВ» РХТУ им. Менделеева 2004г.
Н. БОБЫЛЁВ «ФИЗИЧЕСКИЕ СВОЙСТВА НАИБОЛЕЕ ИЗВЕСТНЫХ ХИМИЧЕСКИХ ВЕЩЕСТВ» РХТУ им. Менделеева 2004г.