Как расшифровать цифры: 10 популярных кодов и шифров

Содержание

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры
Цифровые шифры
Как расшифровать код или шифр?

Стандартные шифры

ROT1

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Лбл еёмб, рспдсбннйту?

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh.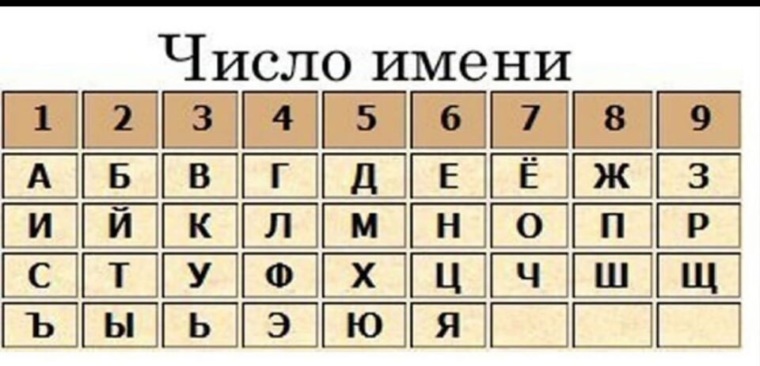

Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

def split_len(seq, length):
   return [seq[i:i + length] for i in range(0, len(seq), length)]
def encode(key, plaintext):
   order = {
      int(val): num for num, val in enumerate(key)
   }
ciphertext = ''

for index in sorted(order.keys()):
   for part in split_len(plaintext, len(key)):
      try:ciphertext += part[order[index]]
         except IndexError:
            continue
   return ciphertext
print(encode('3214', 'HELLO'))

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

•−−   −•− −−− −• −•−• •   ••• − •− − −••− ••   • ••• − −••−   −•• • −−−− •• ••−• •−• •− − −−− •−• −•−−

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Иербэй йюк ёурбэй нтчйхйцтаъ энщхуж

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для

(k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

зюм иэлруй южжуглёнъ

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

110100001001101011010000101111101101000010110100

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите.

Только нижний регистр.

Попробуйте определить, что здесь написано:

15-6-2-16-13-30-26-16-11 17-18-10-14-6-18

Шифрование публичным ключом

Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать.

Примеры шифраторов и дешифраторов:

Адаптированный перевод «10 codes and ciphers»

Шифр цифрами расшифровка. Шифрование цифрами

Пожалуй, шифр Цезаря один из самых простейших способов шифрования данных. Он использовался Цезарем еще до нашей эры для тайной переписки. И если предложить любому человеку придумать свой алгоритм шифровки, то он, наверняка, «придумает» именно такой способ, ввиду его простоты.

Шифр Цезаря часто называют шифром сдвига . Давайте разберемся, как шифровать данные с помощью этого метода криптографии.

Шифр Цезаря онлайн

Сервис предназначен для шифрования любого текста, используя для этого шифр сдвига (Цезаря). Шифруются только русские буквы, все остальные символы остаются без изменения.

Как шифровать

Предположим, что мы хотим зашифровать слово Россия. Рассмотрим, как для этого можно использовать шифр Цезаря. Для начала, вспомним русский алфавит и пронумеруем буквы по-порядку.

Итак, наше слово Россия. Попробуем его зашифровать. Для этого нам нужно определиться с шагом шифрования. Шаг шифрования или сдвиг — это число, которое указывает на сколько позиций мы будем смещаться влево или вправо по алфавиту. Часто сдвиг называют ключом . Его можно выбрать произвольно. В нашем примере выберем шаг равный 7. Таким образом каждую букву шифруемого слова мы будем смещать вправо (в сторону конца алфавита) на 7 позиций. Буква Р у нас имеет номер 18. Прибавим к 18 наш шаг и получим 25. Значит в зашифрованном слове вместо буквы Р будет буква с номером 25 — Ч. Буква о превратится в букву х. Буква с — в ш и так далее. В итоге после шифрования слово Россия превратится в Чхшшпё.

Р -> Ч
о -> х
с -> ш
с -> ш
и -> п
я -> ё

Задавая шаг шифрования можно зашифровать любой текст.

Как расшифровать

Во-первых, вы можете воспользоваться специально созданным калькулятором на этой странице. В поле для текста вводите зашифрованный текст, а наш сервис дешифрует его, используя все возможные варианты сдвига. На выходе вы получите все полученные результаты и вам останется только выбрать правильный. К примеру, у вас есть зашифрованный шифром Цезаря текст — «З шчхцж аьмцчн хлцчкнцен». Вставляем его в калькулятор и получаем варианты дешифрования, среди которого видим «Я помню чудное мгновенье» со сдвигом 24.

Ну и, естественно, вы можете произвести дешифровку вручную. Но такая расшифровка займет очень много времени.

Моих воспоминаний с детских лет + воображения хватило ровно на один квест: десяток заданий, которые не дублируются.
Но детям забава понравилась, они просили еще квесты и пришлось лезть в инет.

В этой статье не будет описания сценария, легенд, оформления. Но будет 13 шифров, чтобы закодировать задания к квесту.

Шифр №1. Картинка

Рисунок или фото, которое напрямую указывает место, где спрятана следующая подсказка, или намек на него: веник +розетка = пылесос
Усложнение: сделайте паззл, разрезав фото на несколько частей.

Шифр 2. Чехарда.

Поменяйте в слове буквы местами: ДИВАН = НИДАВ

Шифр 3.

Греческий алфавит. Закодируйте послание буквами греческого алфавита, а детям выдайте ключ:

Шифр 4. Наоборот.

Пишете задание задом наперед:

каждое слово:
Етищи далк доп йонсос
или все предложение, или даже абзац:
етсем морком момас в — акзаксдоп яащюуделС. итуп монрев ан ыВ

Шифр 5. Зеркально.

(когда я делала квест своим детям, то в самом начале выдала им «волшебный мешочек»: там был ключ к «греческому алфавиту», зеркало, «окошки», ручки и листы бумаги, и еще всякая ненужная всячина для запутывания. Находя очередную загадку, они должны были сами сообразить, что из мешочка поможет найти отгадку)

Шифр 6. Ребус.

Слово кодируется в картинках:

Шифр 7. Следующая буква.

Пишем слово, заменяя все буквы в нем на следующие по алфавиту (тогда Я заменяется на А, по кругу). Или предыдущие, или следующие через 5 букв:).

ШКАФ = ЩЛБХ

Шифр 8. Классика в помощь.

Я брала стихотворение (и говорила детям, какое именно) и шифр из 2х цифр: № строки № буквы в строке.

Пример:

Пушкин «Зимний вечер»

Буря мглою небо кроет,
Вихри снежные крутя;
То, как зверь, она завоет,
То заплачет, как дитя,
То по кровле обветшалой
Вдруг соломой зашумит,
То, как путник запоздалый,
К нам в окошко застучит.

21 44 36 32 82 82 44 33 12 23 82 28

прочитали, где подсказка? 🙂

Шифр 9. Темница.

В решетку 3х3 вписываете буквы:

Тогда слово ОКНО шифруется так:

Шифр 10. Лабиринт.

Моим детям такой шифр пришелся по душе, он непохож на остальные, потому что не столько для мозгов, сколько на внимание.

Итак:

на длинную нитку/веревку цепляете буквы по порядку, как они идут в слове. Затем веревку растягиваете, закручиваете и всячески запутываете между опорами (деревьями, ножками итд). Пройдя по нитке, как по лабиринту, от 1й буквы до последней, дети узнают слово-подсказку.

А представьте, если обмотать таким образом одного из взрослых гостей!
Дети читают — Следующая подсказка на дяде Васе.
И бегут ощупывать дядю Васю. Эх, если он еще и щекотки боится, то весело будет всем!

Шифр 11. Невидимые чернила.

Восковой свечкой пишете слово. Если закрасить лист акварелью, то его можно будет прочитать.
(есть и другие невидимые чернила.. молоко, лимон, еще что-то.. Но у меня в доме оказалась только свечка:))

Шифр 12. Белиберда.

Гласные буквы остаются без изменений, а согласные меняются, согласно ключу.
например:
ОВЕКЬ ЩОМОЗКО
читается как — ОЧЕНЬ ХОЛОДНО, если знать ключ:
Д Л Х Н Ч
З М Щ К В

Шифр 13. Окошки.

Детям понравилось неимоверно! Они потом этими окошками весь день друг другу послания шифровали.
Итак: на одном листе вырезаем окошки, столько, сколько букв в слове. Это трафарет, его прикладываем к чистому листу и «в окошках» пишем слово-подсказку. Затем трафарет убираем и на оставшемся чистом месте листа пишем много разных других ненужных букв. Прочитать шифр можно, если приложить трафарет с окошками.
Дети сначала впали в ступор, когда нашли лист, испещренный буквами.

Потом крутили туда-сюда трафарет, его же нужно еще правильной стороной приложить!

Шифр 14. Карта, Билли!

Нарисуйте карту и отметьте (Х) место с кладом.
Когда я делала своим квест первый раз, то решила что карта — это им очень просто, поэтому нужно ее сделать загадочней (потом выяснилось, что детям хватило бы и просто карты, чтобы запутаться и бежать в противоположном направлении)…

Это схема нашей улицы. Подсказки здесь — номера домов (чтоб понять, что это вообще наша улица) и хаски. Такая собака живет у соседа напротив.
Дети не сразу узнали местность, задавали мне наводящие вопросы..
Тогда в квесте участвовало 14 детей, поэтому я их обьединила в 3 команды. У них было 3 варианта этой карты и на каждом помечено свое место. В итоге, каждая команда нашла по одному слову:
«ПОКАЖИТЕ» «СКАЗКУ» «РЕПКА»
Это было следующее задание:). После него остались уморительные фото!
На 9ти летие сына не было времени выдумывать квест и я его купила на сайте MasterFuns . . На свой страх и риск, потому что описание там не очень.
Но нам с детьми понравилось, потому что:

недорого (аналог где-то 4х долларов за комплект)
быстро (заплатила — скачала-распечатала — на все про все минут 15-20)
заданий много, с запасом. Ихотя мне не все загадки понравились, но там было из чего выбрать, и можно было вписать свое задание
все оформлено в одном, монстерском, стиле и это придает празднику эффект. Помимо самих заданий к квесту, в комплект входят: открытка, флажки, украшения для стола, приглашения гостям. И все -в монстрах! 🙂
помимо 9ти летнего именинника и его друзей, у меня есть еще 5тилетняя дочка. Задания ей не по силам, но для нее и подружки тоже нашлось развлечение — 2 игры с монстрами, которые тоже были в наборе. Фух, в итоге — все довольны!

Человек – социальное существо. Мы учимся взаимодействовать с другими, наблюдая за их реакцией на наши действия с первых дней жизни. При любом взаимодействии мы используем то, что искусствоведы называют «культурными кодами». А ведь культурные коды – самые сложные в дешифровке, здесь нет специальной программы, которая подскажет, что может значить приподнятая бровь или беспричинные, казалось бы, слёзы; нет однозначного ответа; более того, даже сам «кодирующий» может не знать, что он имел в виду под своим действием! Наука понимать окружающих – это то, что мы постигаем всю жизнь, и чем лучше развито это умение, тем, как правило, гармоничнее складывается общение с окружающими и любая деятельность, в которой нужны согласованные действия.

Изучение криптографии в обеих её ипостасях (шифровка и дешифровка) позволяет научиться находить связь между шифрованным, запутанным, непонятным посланием и смыслом, который в нём таится. Проходя исторический путь от шифра Юлия Цезаря до RSA-ключей, от розеттского камня до эсперанто, мы учимся воспринимать информацию в непривычном нам виде, разгадываем загадки, привыкаем к многовариантности. И главное – учимся понимать: как разных, непохожих на нас людей, так и математико-лингвистические механизмы, которые лежат в основе каждого, абсолютно каждого послания.

Итак, приключенческий рассказ о криптографии для детей, для всех, у кого есть дети, и для всех, кто когда-нибудь был ребёнком.

Трепещут на ветру флаги, ржут разгорячённые кони, бряцают доспехи: это Римская империя обнаружила, что в мире ещё есть кто–то, кого они не завоевали. Под командованием Гая Юлия Цезаря находится огромная армия, которой надо быстро и точно управлять.

Шпионы не дремлют, враги готовятся перехватить посланников императора, чтобы узнать все его блестящие планы. Каждый кусок пергамента, попадающий не в те руки – это вероятность проиграть сражение.

Но вот захвачен посланник, злоумышленник разворачивает записку… и ничего не понимает! «Наверное, – чешет он в затылке, – это на каком–то неизвестном языке…». Рим торжествует, его планы в безопасности.

Что же такое шифр Цезаря? Самый простой его вариант – это когда мы вместо каждой буквы ставим следующую по алфавиту: вместо «а» – «б», вместо «е» – «ж», а вместо «я» – «а». Тогда, например, «Я люблю играть» станет «А мявмя йдсбуэ». Давайте посмотрим на табличку, сверху в ней будет буква, которую шифруем, а снизу – на которую заменяем.

Алфавит как бы «сдвинут» на одну букву, правда? Поэтому этот шифр ещё называют «шифром сдвига» и говорят «используем шифр Цезаря со сдвигом 10» или «со сдвигом 18». Это значит, что надо «сдвинуть» нижний алфавит не на 1, как у нас, а, например, на 10 – тогда у нас вместо «а» будет «й», а вместо «у» – «э».

Сам Цезарь использовал этот шифр со сдвигом 3, то есть его таблица шифрования выглядела вот так:

Точнее, она бы так выглядела, если бы Цезарь жил в России. В его случае алфавит был латинский.

Такой шифр достаточно легко взломать, если вы профессиональный шпион или Шерлок Холмс. Но он до сих пор подходит для того, чтобы хранить свои маленькие секреты от посторонних глаз.

Вы и сами можете устроить свой маленький домашний заговор. Договоритесь о своём числе сдвига, и вы сможете оставлять друг другу шифрованные записки на холодильнике о сюрпризе на чей-нибудь день рождения, отправлять шифрованные сообщения и, может быть, если случится длинная разлука, даже писать друг другу тайные, кодированные письма!

Но вся история криптографии – это история борьбы между искусством зашифровывать послания и искусством их расшифровывать. Когда появляется новый способ закодировать сообщение, находятся те, кто пытаются этот код взломать.

Что такое «взломать код»? Это значит – придумать способ его разгадать, не зная ключа и смысла шифра. Шифр Цезаря тоже когда-то был взломан – так называемым «методом частотного анализа». Посмотрите на любой текст – гласных в нём гораздо больше, чем согласных, а «о» гораздо больше, чем, например, «я». Для каждого языка можно назвать самые часто и редко используемые буквы. Надо только найти, какой буквы больше всего в зашифрованном тексте. И скорее всего это будет зашифрованная «о», «е», «и» или «а» – самые часто встречающиеся буквы в русских словах. А как только ты знаешь, какой буквой обозначили, например, «а», ты знаешь, и на сколько «сдвинут» шифрованный алфавит, а значит, можешь расшифровать весь текст.

Когда разгадку кода Цезаря узнал весь мир, криптографам пришлось придумать что-нибудь помощнее. Но, как часто бывает, люди не стали изобретать что–то совсем новое, а усложнили уже имеющееся. Вместо того, чтобы шифровать все буквы по одному и тому же сдвинутому алфавиту, в тайных посланиях их стали использовать несколько. Например, первую букву шифруем по алфавиту со сдвигом 3, вторую – со сдвигом 5, третью – со сдвигом 20, четвертую – снова со сдвигом 3, пятую – со сдвигом 5, шестую – со сдвигом 20 и так далее, по кругу. Такой шифр называют полиалфавитным (то есть многоалфавитным). Попробуйте, так ваш шифр уже может разгадать только тот, кто посвящён в тайны криптографии!

Казалось бы, злоумышленники должны были запутаться и тайны должны были навсегда остаться тайнами. Но если шифр один раз был взломан, то и любые более сложные его варианты тоже будут однажды взломаны.

Давайте представим, что кто–то зашифровал послание двумя алфавитами. Первая буква – со сдвигом 5, вторая – со сдвигом 3, третья – снова 5, четвертая снова 3 – как на табличке ниже.

Мы можем разделить все зашифрованные буквы на две группы: буквы, зашифрованные со сдвигом 5 (1, 3, 5, 7, 9, 11, 13, 15, 17, 19) и буквы, зашифрованные со сдвигом 3 (2, 4, 6, 8, 10, 12, 14, 16, 18, 20). И внутри каждой группы искать, какие буквы встретились нам чаще остальных – так же, как в шифре Цезаря, только мороки побольше.

Если шифровщик использовал три алфавита, то мы разделим буквы на три группы, если пять – то на пять. А дальше снова идет в ход тот же самый частотный анализ.

Можно задать вопрос – откуда дешифраторы знали, что алфавитов три, а не, например, пять? На самом деле они не знали. И перебирали все возможные варианты. Поэтому дешифровка занимала гораздо больше времени, но все же была возможной.

В криптографии сообщение, которое надо передать, называется «открытым текстом», а зашифрованное сообщение – «шифрованным текстом». И правило, по которому текст зашифрован, называется «ключом шифра».

Незаметно подкрался XX век. Человечество всё больше надеется на машины: поезда заменяют повозки, радио появляется почти в каждом доме, и уже встали на крыло первые самолеты. И шифровку тайных планов в конце концов тоже передают машинам.

Во время Второй мировой войны было изобретено очень много машин для шифрования сообщений, но все они опирались на идею того, что полиалфавитный шифр можно ещё больше запутать. Запутать настолько, что, хотя по идее его и можно будет разгадать, на практике это ни у кого не получится. Запутать настолько, насколько это способна сделать машина, но не способен человек. Самая известная из таких шифровальных машин – «Энигма», использовавшаяся Германией.

theromanroad.files.wordpress.com

Но, пока самой главной тайной Германии была конструкция «Энигмы», самой главной тайной её противников было то, что к середине войны все страны уже «Энигму» разгадали. Если бы об этом стало известно в самой Германии, они бы начали придумывать что-то новое, но до конца войны они верили в идеальность своей шифровальной машины, а Франция, Англия, Польша, Россия читали тайные немецкие сообщения как открытую книгу.

Всё дело в том, что польский ученый Мариан Реевский однажды подумал о том, что раз придумали машину для шифровки сообщений, то можно придумать и машину для расшифровки, и первый свой образец называл «Бомба». Не из-за «взрывного» эффекта, как можно было бы подумать, а в честь вкусного, круглого пирожного.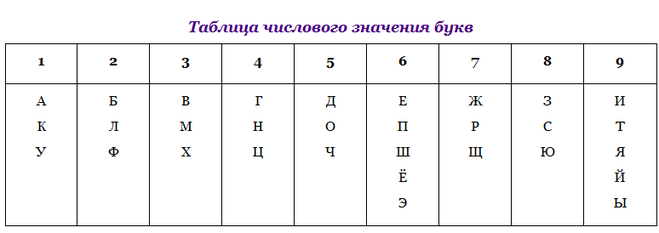

Потом математик Алан Тьюринг построил на его основе машину, которая полностью расшифровывала код «Энигмы», и которую, между прочим, можно считать первым прародителем наших современных компьютеров.

Самый сложный код за всю Вторую мировую придумали американцы. На каждый боевой корабль США был откомандирован… индеец. Их язык был настолько непонятен и малоизучен, звучал так странно, что дешифровщики не знали, как и подступиться, и флот США безбоязненно передавал информацию на языке индейского племени чокта.

Вообще, криптография – это же не только о том, как загадать загадку, но и о том, как её разгадать. Не всегда такие загадки специально придумывают люди – иногда их подбрасывает сама история. И одной из главных загадок для криптографов долгое время была загадка древнеегипетского языка.

Никто не знал, что же значат все эти иероглифы. Что египтяне имели в виду, рисуя птиц и скарабеев. Но в один счастливый день французская армия обнаружила в Египте «Розеттский камень».

На этом камне была надпись – одна и та же, на древнегреческом, египетском буквенном (демотический текст) и египетском иероглифическом. Историки того времени хорошо знали древнегреческий, поэтому что же написано на камне они узнали быстро. Но главное, что, зная перевод, они смогли раскрыть тайны древнего египетского языка. Демотический текст был расшифрован достаточно быстро, а вот над иероглифами историки, лингвисты, математики, криптографы ломали голову долгие годы, но в конце концов всё-таки разгадали.

И это была большая победа криптографов – победа над самим временем, которое надеялось спрятать от людей их историю.

Но среди всех этих разгаданных шифров есть три особенных. Один – это метод Диффи – Хеллмана. Если маленькое сообщение зашифровать этим методом, то, чтобы его расшифровать, надо взять все компьютеры в мире и занять их этим на много-много лет. Именно он используется сегодня в Интернете.

Второй – это квантовое шифрование. Оно, правда, ещё не совсем придумано, зато, если люди сделают квантовые компьютеры такими, как о них мечтают, то такой шифр будет знать, когда его пытаются расшифровывать .

А третий особенный шифр – это «книжный шифр». Его удивительность в том, что им просто что-то зашифровать и непросто – расшифровать. Два человека выбирают одну и ту же книгу, и каждое слово из своего письма в ней ищут и заменяют тремя цифрами: номер страницы, номер строки и номер слова в строке. Это очень просто сделать, правда? А разгадать совсем не просто: откуда шпиону знать, какую книгу вы выбрали? И самое главное, компьютеры в этом деле тоже особо не помогут. Конечно, если подключить очень много умных людей и очень много мощных компьютеров, такой шифр не устоит.

Но есть главное правило безопасности. Её, этой безопасности, должно быть столько, чтобы зашифрованное послание не стоило тех огромных усилий, которые надо потратить на её расшифровку. То есть чтобы злодею – шпиону пришлось потратить столько сил, чтобы разгадать ваш код, сколько он не готов тратить на то, чтобы узнать ваше сообщение. И это правило работает всегда и везде, как в дружеских школьных переписках, так и в мире настоящих шпионских игр.

Криптография – это искусство загадывать и разгадывать загадки. Искусство сохранить тайны, и искусство их раскрывать. С криптографией мы учимся понимать друг друга и придумываем, как сохранить что-то важное для себя в безопасности. А чем лучше мы умеем и то и другое, тем спокойнее и деятельнее может быть наша жизнь.

Воспользоваться старой и малоизвестной системой записи. Даже римские цифры не всегда бывает легко прочитать, особенно с первого взгляда и без справочника. Мало кто сможет «с лёта» определить, что в длинной строчке MMMCDLXXXIX скрывается число 3489.

С римской системой счисления знакомы многие, поэтому ее нельзя назвать надежной для шифрования. Гораздо лучше прибегнуть, например, к греческой системе, где цифры также обозначаются буквами, но букв используется намного больше. В надписи ОМГ, которую легко принять за распространенное в интернете выражение эмоций, может быть спрятано записанное по-гречески число 443. Буква «О микрон» соответствует числу 400, буквой «Мю» обозначается 40, ну а «Гамма» заменяет тройку.

Недостаток подобных буквенных систем в том, что они зачастую требуют экзотических букв и знаков. Это не составляет особого труда, если ваш шифр записан ручкой на бумаге, но превращается в проблему, если вы хотите отправить его, скажем, по электронной почте. Компьютерные шрифты включают в себя греческие символы, но их бывает сложно набирать. А если вы выбрали что-то еще более необычное, вроде старой кириллической записи или египетских числовых , то компьютер просто не сможет их передать.

Для таких случаев можно рекомендовать простой способ, которым в России в старые времена пользовались все те же бродячие торговцы — коробейники и офени. Для успешной торговли им было жизненно необходимо согласовывать между собой цены, но так, чтобы об этом не узнал никто посторонний. Поэтому коробейники и разработали множество хитроумных способов шифровки.

С цифрами они обходились следующим образом. Вначале нужно взять слово в котором есть десять различных букв, например «правосудие». Затем буквы нумеруются от единицы до нуля. «П» становится знаком для единицы, «в» — для четверки, и так далее. После этого любое число можно записывать буквами вместо цифр по обычной десятичной системе. Например, год 2011 записывается по системе офеней как «реепп». Попробуйте сами , спрятано в строчке «а,пвпоирс».

«Правосудие» — не единственное слово русского языка, подходящее для этого метода. «Трудолюбие» годится ничуть не хуже: в нем также десять неповторяющихся букв. Вы вполне можете и самостоятельно поискать другие возможные основы.

Не зря историю Египта считают одной из самых таинственных, а культуру одной из высокоразвитых. Древние египтяне, не в пример многим народам, не только умели возводить пирамиды и мумифицировать тела, но владели грамотой, вели счет, вычисляли небесные светила, фиксируя их координаты.

Десятичная система Египта

Современная десятичная появилась чуть более 2000 лет назад, однако египтяне владели ее аналогом еще во времена фараонов. Вместо громоздких индивидуальных буквенно-знаковых обозначений числа они использовали унифицированные знаки – графические изображения, цифры. Цифры они делили на единицы, десятки, сотни и т.д., обозначая каждую категорию специальным иероглифом.

Как такового правила цифр не было, то есть их могли в любом порядке, например, справа налево, слева направо. Иногда их даже составляли в вертикальную строку, при этом направление чтения цифрового ряда задавалось видом первой цифры – вытянутая (для вертикального чтения) или сплюснутая (для горизонтального).

Найденные при раскопках древние папирусы с цифрами свидетельствуют, что египтяне уже в то время рассматривали различные арифметические , проводили исчисления и при помощи цифр фиксировали результат, применяли цифровые обозначения в области геометрии. Это значит, что цифровая запись была распространенной и общепринятой.

Цифры нередко наделялись магическим и знаковым значением, о чем свидетельствует их изображение не только на папирусах, но и на саркофагах, стенах усыпальниц.

Вид цифры

Цифровые иероглифы были геометричны и состояли только из прямых. Иероглифы выглядели достаточно просто, например цифра «1» у египтян обозначалась одной вертикальной полоской, «2» — двумя, «3» — тремя. А вот некоторые цифры, написанные , не поддаются современной логике, примером служит цифра «4», которая изображалась как одна горизонтальная полоска, а цифра «8» в виде двух горизонтальных полосок. Самыми сложными в написании считались цифры девять и шесть, они состояли из характерных черт под разным наклоном.

Долгие годы египтологи не могли расшифровать эти иероглифы, полагая, что перед ними буквы или слова.

Одними из последних были расшифрованы и переведены иероглифы, обозначающих массу, совокупность. Сложность была объективной, ведь некоторые цифры изображались символично, к примеру, на папирусах человек, изображенный с поднятыми , обозначал миллион. Иероглиф с изображением жабы означал тысячу, а личинки — . Однако вся система написания цифр была систематизированной, очевидно – утверждают египтологи – что иероглифы упрощались. Вероятно, их написанию и обозначению обучали даже простой народ, потому как обнаруженные многочисленные торговые грамоты мелких лавочников были составлены грамотно.

Во дворе здания ЦРУ в Лэнгли стоит S-образная медная плита с зашифрованным текстом. Это самый известный элемент скульптуры «Криптос», её авторы — скульптор Джеймс Санборн и Эд Шейдт, отставной глава криптографического отдела ЦРУ. Они придумали шифр, разгадать который трудно, но вполне реально. По крайней мере, им так казалось.

По замыслу авторов, «Криптос» олицетворяет процесс сбора информации. Шифр «Криптоса» — 869 символов, поделённых на четыре части. Создатели предполагали, что на решение первых трёх частей уйдёт около семи месяцев, на решение всей задачи — примерно семь лет. 23 года спустя полной расшифровки всё ещё нет. «Криптосом» занимаются любители (с 2003 года на Yahoo! существует группа из примерно 1500 человек) и профессионалы (из ЦРУ и АНБ) — их задачу осложняют намеренные ошибки, допущенные Санборном и Шейдтом (частично чтобы запутать людей, частично из эстетических соображений).
Считается, что Санборн — единственный человек на планете, знающий разгадку «Криптоса». Скульптор рассказывает, что люди, помешанные на созданном им шифре, звонят и говорят ужасные вещи: «Они называют меня прислужником дьявола, ведь у меня есть секрет, которым я ни с кем не делюсь». Санборн говорит, что в случае его смерти ответ обязательно перейдет к кому-то другому, но добавляет, что не совершенно не расстроится, если правильное решение навсегда останется тайной.

Убийца, про которого всё ещё ничего не известно, отправлял в калифорнийские газеты зашифрованные письма, обещая, что в них найдутся ключи к установлению его личности. Первое послание Зодиака (август 1969-го) состояло из трёх частей и 408 символов, быстрее всех его расшифровала обычная калифорнийская семейная пара. Смысл письма сводился к тому, что убивать людей гораздо интереснее, чем животных, ведь человек — самое опасное существо на планете. «Я попаду в рай, где те, кого я убил, станут моими рабами», — гласила записка. Эта была последняя успешная попытка расшифровать криптограмму Зодиака. Тайной остаётся содержание открытки с кодом из 340 знаков, пришедшей три месяца спустя в редакцию San Francisco Chronicle. «Можете напечатать его на первой странице? Мне ужасно одиноко, когда меня не замечают», — просил убийца в сопутствующем письме. Именно этот шифр изображён на постере фильма Дэвида Финчера «Зодиак».

Через несколько дней Зодиак прислал ещё одно письмо, в котором зашифровал свое имя, — оно также осталось неразгаданным. Затем было письмо, в котором убийца угрожал взорвать школьный автобус. К нему он приложил карту и шифр — с их помощью якобы можно было найти бомбу, что планируется использовать для теракта. С этим шифром тоже никто не справился, но и взрыв не произошёл. Попытки разгадать коды Зодиака продолжаются. В 2011-м криптограф-любитель Кори Старлипер заявил, что расшифровал сообщение из 340 символов, и нашёл в нём признание Артура Ли Аллена, когда-то проходившего главным подозреваемым по делу Зодиака, но отпущенного за неимением доказательств. Про Старлипера написали многие газеты, но быстро выяснилось, что его метод не выдерживает никакой критики.

Фестский диск. Считается, что иероглифические надписи на Фестском диске предположительно принадлежат минойской цивилизации, жившей на острове Крит. Глиняный диск с иероглифами, нанесенными на него с двух сторон в виде спирали, обнаружили в 1908 году. Специалисты определили, что на диске есть 45 разных иероглифов, и некоторые из них похожи на знаки, используемые в раннедворцовый период.

Памятник пастуха 18 века в графстве Стаффордшир, Англия. На нем есть странная последовательность букв DOUOSVAVVM – код, который не удается расшифровать уже более 250 лет. Автор этого шифра неизвестен, некоторые полагают, что этот код может быть подсказкой, оставленной рыцарями-тамплиерами относительно местонахождения Святого Грааля. Многие из величайших умов пытались расшифровать этот код и потерпели неудачу, включая Чарльза Диккенса и Чарльза Дарвина.

Линейное письмо. Также было найдено на Крите и названо в честь британского археолога Артура Эванса. В 1952 году Майкл Вентрис расшифровал линейное письмо B, которое использовалось для шифровки микенского языка – самого древнего из известных вариантов греческого. Но линейное письмо A разгадано лишь частично, при этом разгаданные фрагменты написаны на каком-то не известном науке языке, не связанном ни с одним из известных языков.

В 1933 году генералу Вану из Шанхая, Китай, были выданы семь золотых слитков . На слитках были выгравированы рисунки, надписи на китайском языке и криптограммы, частично латинскими буквами. Предположительно, это сертификаты, выданные американским банком. В надписях на китайском языке говорится о сделке, сумма которой превышает 300 миллионов долларов США.

Джон Бирн (John F. Byrne) придумал метод шифрования чаошифр в 1918 году. Бирн считал его очень простым, но все же сложным для расшифровки, и в течение 40 лет он безуспешно пытался заинтересовать американское правительство своим изобретением. Он даже предложил награду тому, кто сможет разгадать его шифр, но за наградой никто так и не обратился. Только в прошлом году его семья передала все бумаги относительно шифра в музей, и специалистам удалось разобраться в его методе.

Сигнал «Wow!» — сильный узкополосный космический радиосигнал, зарегистрированный доктором Джерри Эйманом 15 августа 1977 г. во время работы на радиотелескопе «Большое Ухо» в Университете штата Огайо. Под этим названием Сигнал и запечатлен в истории «Программы по Поиску Внеземных цивилизаций», как до сих пор нерасшифрованный.

Британские математики по-своему участвовали в подводных боях Второй мировой. На полпути между Оксфордом и Кембриджем, в городке Милтон-Кинс, в разгар войны было устроено нечто вроде института, где Алан Тьюринг и другие ученые-знаменитости трудились над взломом кода, который в Германии применяли для связи с подлодками. Немецкие шифровщики использовали аппарат, похожий на печатную машинку с двумя клавиатурами: одна обычная, другая с лампочками. Когда радистка ударяла пальцем по клавише, лампочка вспыхивала под какой-нибудь другой буквой. Эту букву и следовало дописать к шифрованной версии сообщения. Не имея ни одного образца «Энигмы» под рукой, Тьюринг сумел понять принцип работы машины и построить свой дешифратор на основе одних логических рассуждений. Британский историк Хинсли даже заявил, что прорыв в криптоанализе приблизил конец Второй мировой на два, если не на четыре года. На исключительную роль, которую сыграл взлом кода «Энигма» в победе над нацистами, ссылалась и королева Великобритании Елизавета Вторая, когда посмертно помиловала математика несколько месяцев назад. В 1952 году Тьюринга приговорили к химической кастрации за гомосексуализм, после чего ученый покончил жизнь самоубийством.

Йотунвиллур. Рунических надписей — считанные тысячи: на порядки меньше текстов, чем оставила после себя классическая античность. И то речь обычно о коротких обрывочных фразах на дощечках или на камнях. Йонас Нордби, аспирант-лингвист из университета Осло, сосредоточил внимание на 80 зашифрованных: если пытаться прочесть их как есть, выйдет бессмыслица. Девять, как оказалось, используют довольно простой, по меркам современной криптографии, алгоритм — автор исследования называет его Jotunvillur: руну заменяют той, название которой («имя руны») оканчивается на нужную букву. Зачем так скрытничать, понятно в отдельных случаях. Одна из надписей на дощечках, прочитанных Нордби, гласит «Поцелуй меня». Если учесть, что и адресат, и отправитель сообщения должны были как минимум уметь читать, то, вероятно, оба были мужчинами.

В годы Второй мировой войны британская армия нередко использовала голубей для передачи зашифрованных посланий. В 2012 году житель графства Суррей (юг Англии) нашёл в трубе своего дома останки птицы, к лапе которой был прикреплён контейнер с сообщением. Текст предназначался некоему XO2 и был подписан «W Stot Sjt». Изучив сообщение, эксперты Британского центра правительственной связи пришли к выводу, что без доступа к книгам кодов, использованных при создании шифра, найти правильное решение практически невозможно. «Подобные сообщения создавались так, чтобы их могли прочитать только отправитель и получатель. Если мы не узнаем хоть что-то о том, кто написал это письмо или кому оно предназначалось, мы не сможем его расшифровать», — заявил анонимный работник Центра правительственной связи в интервью BBC.

1 декабря 1948 года на пляже Сомертон в Аделаиде нашли труп человека . На теле не было следов насилия, всё, что при нём оказалось, — сигареты, коробок спичек, пачка жвачки, расчёска, билет на автобус и билет на поезд. Патологоанатом, проводивший вскрытие, не сумел определить точную причину его смерти, но предположил, что жертву, скорее всего, отравили ядом, следы которого исчезают из организма уже через несколько часов. Полтора месяца спустя полиция обнаружила на вокзале Аделаиды чемодан, по всей видимости, принадлежавший убитому. Внутри лежали разные инструменты и одежда с оторванными ярлыками — в том числе брюки с секретным карманом, в котором нашли вырванный из книги клочок бумаги с надписью «Tamam Shud». Нужной книгой оказалось чрезвычайно редкое издание сборника поэзии Омара Хайяма. На последней странице карандашом был написан шифр, разгадать который не могут уже больше 60 лет. В 1978-м Министерство обороны Австралии выступило с заявлением: это может быть шифр, это может быть бессмысленный набор символов, сказать точно невозможно. С 2009-го попытки расшифровать криптограмму ведутся в университете Аделаиды. Исследователи пришли к выводу, что это действительно некий шифр, но решения до сих пор нет ни у шифра, ни у самого дела «Таман Шуд» — одной из самых известных тайн в истории Австралии.

В первом издании книги Codes and Ciphers («Коды и шифры») английского картографа и криптографа русского происхождения Александра Д’Агапеева был напечатан шифр, до сих пор остающийся неразгаданным. Уже после выхода книги автор признался, что забыл правильный ответ. В следующих изданиях «Кодов и шифров» криптограммы не было. Доказано, что в основе шифра Д’Агапеева действительно лежит некая система (то есть это не просто беспорядочный набор символов), однако он оказался слишком сложен. В начале 1950-х журнал The Cryptogram объявил награду за расшифровку кода, но правильный ответ всё ещё не найден.

14 июля 1897-го знаменитый английский композитор Эдвард Элгар отправил записку Дорабелле — так он называл свою подругу Дору Пенни. «Мисс Пенни», — гласила надпись на одной стороне карточки. На другой был трехстрочный шифр из 87 символов. Дора не смогла расшифровать послание, и оно пролежало в ящике её стола 40 лет, прежде чем его перепечатали в книге воспоминаний Пенни об Элгаре. Расшифровывая письмо композитора, одни пытались обойтись простейшим методом замены символов на буквы, другие приходили к выводу, что здесь вообще скрыты не слова, а мелодия. У одних получались сообщения, в которых не понятно абсолютно ничего, у других — предельно лиричные тексты, полные мечтательности и любви. Окончательного решения нет до сих пор; ничем закончился и конкурс по расшифровке, проведённый в 2007-м в честь 150-летия Элгара.

Скрижали Джорджии — крупный гранитный монумент в округе Элберт в штате Джорджия, США. Памятник содержит длинную надпись на 8 современных языках, а на вершине памятника имеется более краткая надпись на 4 древних языках: аккадском, классическом греческом, санскрите и древнеегипетском. Монумент не содержит зашифрованных посланий, но его цель и происхождение остаются загадкой. Он был воздвигнут человеком, личность которого так и не удалось установить.

Рукопись Войнича, которую часто называют самой таинственной в мире книгой. В рукописи использован уникальный алфавит, в ней около 250 страниц и рисунки, изображающие неведомые цветы, обнаженных нимф и астрологические символы. Впервые она появилась в конце XVI века, когда император Священной Римской империи Рудольф II купил ее в Праге у неизвестного торговца за 600 дукатов (около 3,5 кг золота, сегодня более 50 тысяч долларов). От Рудольфа II книга перешла к дворянам и ученым, а в конце XVII века исчезла. Манускрипт вновь появился примерно в 1912 году, когда его купил американский книготорговец Вилфрид Войнич. После его смерти рукопись была передана в дар Йельскому университету. Британский ученый Гордон Рагг считает, что книга – искусная мистификация.

В тексте есть особенности, не свойственные ни одному из языков. С другой стороны, некоторые черты, например, длина слов, способы соединения букв и слогов, похожи на существующие в настоящих языках. “Многие считают, что все это слишком сложно для мистификации, чтобы выстроить такую систему, какому-нибудь безумному алхимику потребовались бы годы”, – говорит Рагг. Однако Рагг показывает, что добиться такой сложности можно было легко, используя шифровальное устройство, придуманное примерно в 1550 году и названное сеткой Кардана. В этой таблице символов слова создаются передвижением карточки с прорезанными в ней отверстиями. Благодаря пробелам, оставленным в таблице, слова получаются разной длины. Накладывая такие решетки на таблицу слогов манускрипта, Рагг создал язык, которому присущи многие, если не все, особенности языка рукописи. По его словам, на создание всей книги хватило бы трех месяцев.

Вдохновившись рукописью Войнича, в 1981 году итальянский дизайнер и архитектор Луиджи Серафини опубликовал свой альбом , выдержанный в том же стиле: 360 страниц текста на неизвестном языке и миниатюр в духе средневекового естественно-научного трактата. Только если исторический манускрипт и можно подозревать в том, что он описывает некую реальную флору и фауну, то у Серафини лошади плавно переходят в гусениц, а занятые сексом юноша и девушка на раскадровке превращаются в крокодила.

Во всех интервью Серафини утверждает, что текст лишен смысла, а в последовательности миниатюр не нужно искать логики — что, разумеется, только подогревает интерес к книге у энтузиастов-криптологов.

Ронго-ронго, кохау ронгоронго — деревянные дощечки с письменами жителей острова Пасхи. В настоящее время не ясно, представляют ли каждый символ отдельное слово или слог. Все ронго-ронго сделаны из дерева торомиро. На сегодня в музеях мира сохранилось всего около 25 «дощечек». Традиционно они нумеруются буквами латинского алфавита, что однако не является единственным способом обозначения «таблиц», среди которых присутствует один жезл, две надписи на нагрудном украшении реимиро, а также надпись на табакерке и на фигуре тангата ману. Иероглифы — частично символические, частично — геометрические, всего около восьмисот различных знаков (по каталогу Бартеля).

Криптограммы Бейла — 3 зашифрованных сообщения, несущих в себе информацию о местонахождении клада из золота, серебра и драгоценных камней, зарытого якобы на территории Виргинии неподалеку от Линчберга партией золотоискателей под предводительством Томаса Джефферсона Бейла. Цена ненайденного клада в пересчете на современные деньги должна составлять около 30 млн. долларов.

Тelegraf

5.4 Числовые шифры . Основы классической криптологии. Секреты шифров и кодов

Ни для кого не секрет, что нашу современную жизнь представить без цифр просто невозможно. С их помощью не только обозначаются номера домов и квартир или указываются цены в магазинах. Перечислить все возможные сферы применения этих десяти символов просто невозможно.

Вполне естественно, что цифры и числа нашли широкое применение и в криптографии. Так, например, отдельными числами можно заменять буквы, создавая шифры, которые трудно разгадать. Такие шифры, которые специалисты называют числовыми, относятся к одним из самых распространенных и интересных шифров. На первый взгляд криптограммы, созданные с помощью числовых систем шифрования, выглядят как набор ничего не значащих цифр.

Простой числовой шифр

Перед тем как приступить к созданию шифрованных сообщений с помощью простого числового шифра, необходимо составить шифровальную таблицу. В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа. При этом первую букву можно обозначить произвольно выбранным числом, а каждую последующую букву надо обозначить числом, большим, чем предыдущее, на 1,2 или 3.

Например, в русском алфавите букву А можно обозначить числом 27, а числа, предназначенные для обозначения каждой из последующих букв алфавита, увеличивать на 2. В таком случае шифровальная таблица будет выглядеть так:

В качестве примера зашифруем с помощью этой таблицы открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Вместо буквы С запишем соответствующее ей в таблице число 61. Вместо буквы Е запишем соответствующее ей число 37, вместо буквы К — число 47 и так далее. В результате получится следующая криптограмма:

61 37 47 59 37 63 53 55 37 61 55 55 29 77 37 53 43 37

Для большей скрытности этот текст можно произвольно разделить на группы цифр, например вот так:

6137 4759 3763 5355 3761 5555 2977 3753 4337

Перед расшифровкой полученный в данном случае шифрованный текст надо разбить на пары цифр, а затем с помощью приведенной выше шифровальной таблицы заменить цифры на соответствующие буквы.

Шифр гласных букв

Не представляет особых трудностей шифрование сообщений с помощью так называемого шифра гласных букв.

При использовании такого шифра гласные буквы в алфавите нумеруются цифрами от 1 до 9. При этом, например, в русском алфавите буква А обозначается цифрой 1, буква Е — цифрой 2, буква И — цифрой 3 и так далее. Затем каждой согласной букве присваивается свой номер, который определяется ее положением относительно ближайшей к ней с левой стороны в алфавите гласной буквы.

Так, например, буква Б — первая согласная буква, расположенная справа от буквы А имеющей номер 1. Поэтому букве Б присваивается число 11. Буква Д — четвертая справа от буквы А, ее обозначают числом 14. Буква Н — пятая справа от гласной буквы И, обозначенной числом 3. Поэтому букве Н должно соответствовать число 35. В соответствии с этим правилом выбираются числа, которыми будут заменены остальные буквы алфавита.

Для быстрого создания шифрованных сообщений с помощью шифра гласных букв можно составить вот такую шифровальную таблицу:

Теперь достаточно в открытом тексте заменить буквы на соответствующие числа, записываемые через точку, и шифровка готова.

В качестве примера попробуем с помощью приведенной выше таблицы зашифровать открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ Сначала необходимо заменить букву С на соответствующее ей число 43, затем букву Е — на число 2, букву К — на число 32 и так до конца текста. В результате зашифрованное сообщение будет выглядеть вот так

43.2.32.42.2.44.35.4.2 43.4.4.11.56.2.35.3.2

Или без пробелов:

43.2.32.42.2.44.35.4.2.43.4.4.11.56.235.3.2

Расшифровка такой криптограммы при использовании заранее составленной таблицы также не будет долгой и затруднительной.

Календарный шифр

Для создания криптограмм с помощью календарного шифра сначала также надо составить шифровальную таблицу. В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа от 1 до 32. В таком случае наша таблица будет выглядеть так:

В качестве примера зашифруем с помощью календарного шифра открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Вместо буквы С запишем соответствующее ей в таблице число 18. Вместо буквы Е запишем соответствующее ей число 6, вместо буквы К — число 11 и так далее. В результате получится следующая криптограмма:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Но на этом процесс шифрования не заканчивается. Теперь выберем какой-либо месяц календаря и каждый день недели обозначим соответствующей буквой. Например, понедельнику будет соответствовать буква П, вторнику — буква В, среде — буква С, четвергу — буква 4, пятнице — буква П, субботе — буква С, воскресенью — буква В.

Поскольку названия некоторых дней недели начинаются с одинаковых букв, для их различия можно применить цифры. Например, понедельнику будет соответствовать сочетание П1, вторнику — сочетание В1, среде — сочетание С1, четвергу — буква Ч, пятнице сочетание П2, субботе — сочетание С2, воскресенью — сочетание В2.

Шифрование открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ начнется с первой буквы, которой в таблице соответствует число 18. Если 18-е число выбранного месяца выпадет на четверг третьей недели, то первую букву в открытом тексте, а именно букву С, следует заменить на сочетание 43. Таким образом, шифрованное сообщение будет начинаться со знаков 43. Если же 18-е число выбранного месяца выпадет на пятницу третьей недели, то сообщение будет начинаться с сочетания П23. В том случае, когда 18-е число окажется, например, понедельником четвертой недели, то шифровку начнут знаки П14. Таким же образом следует заменить остальные буквы открытого текста.

Например, если для шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ выбрать календарь на март 2012 года, то порядок шифрования будет следующим.

Сначала в соответствии с приведенной выше таблицей необходимо перевести буквы в цифры. В результате из открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ получим:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Теперь с помощью календаря на март 2012 года следует зашифровать числа в дни недели.

Число 18 в марте 2012 года — воскресенье третьей недели, поэтому его надо обозначить как В23.

Число 6 — вторник второй недели, этот день обозначается как В12.

Число 11 в марте 2012 года — воскресенье второй недели, поэтому его надо заменить на сочетание В22.

Для удобства в работе, после того как будут выбраны месяц и год шифровальную таблицу можно дополнить строкой, в которой будет непосредственно указано, на какие сочетания букв и цифр следует заменять соответствующие буквы открытого текста.

В результате шифровальная таблица с использованием календаря на март 2012 года примет следующий вид:

Теперь с помощью такой таблицы зашифровать любое сообщение будет очень просто. Достаточно всего лишь для каждой буквы открытого текста найти соответствующее сочетание знаков для шифровки и выполнить замену. Так, например, открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ после шифрования с помощью календарного шифра с использованием календаря на декабрь 2005 года будет преобразован вот в такую криптограмму:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12 В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Или без пробелов:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12.В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Дешифровка такого сообщения производится в обратном порядке. Сначала дни недели переводятся в числа месяца, а затем — в буквы открытого текста Естественно, для расшифровки получателю необходимо знать месяц и год, используемые в шифре. Если же заранее составить приведенную выше таблицу, то процесс расшифровки займет всего лишь несколько минут.

Наблюдательный читатель заметит, что в приведенной таблице для обозначения букв алфавита используются 32 числа, хотя в каждом месяце года дней не более, чем 31. Все правильно. Однако в данной таблице ошибок нет. Просто при применении календарного шифра используется маленькая хитрость, заключающаяся в том, что недостающие дни берутся как бы из следующего месяца.

Если посмотреть на букву Я, которая имеет в таблице порядковый номер 32, то она обозначена сочетанием В25. А это означает воскресенье пятой недели. В то же время в календаре на декабрь 2005 года мы не найдем такой даты, поскольку последний, 31-й день этого месяца приходится на субботу пятой недели. Но это не страшно. Из таблицы пользователь точно знает, что буква Я заменена на сочетание В25. Точно так же заполняются соответствующие ячейки таблицы при использовании месяцев с меньшим количеством дней, от 28 до 30 дней.

Использование несуществующих дат лишь запутает того, кто без ведома и разрешения отправителя захочет разгадать такую шифровку. Главное, чтобы тот, кому такое сообщение предназначается, знал об этих маленьких хитростях.

5.5. Книжные шифры

Среди специалистов так называемые книжные шифры считаются сравнительно стойкими системами шифрования. Дело в том, что взломать подобный шифр и расшифровать созданную с его помощью криптограмму, не зная книги, использовавшейся при шифровании, неспециалисту практически невозможно.

В то же время созд ание шифрованных сообщений с помощью книжных шифров не представляет особого труда даже для начинающих пользователей. Для этого достаточно взять какую-либо книгу, по определенному правилу обозначить отдельные буквы текста этой книги числами и выполнить замену букв открытого текста на соответствующие им числа. Не обязательно, чтобы книга, используемая для шифрования, была широко известной. Однако она обязательно должна быть у получателя сообщения, который должен знать и правило шифрования.

Необходимо добавить, что во избежание ошибок книга, находящаяся у получателя сообщения и используемая для дешифрования, должна быть точно такой же, что и книга, имеющаяся у отправителя. Это означает, что обе книги должны быть полностью идентичны, с тем же количеством страниц и тем же размещением текста на них.

Простой книжный шифр

Знакомство с книжными шифрами следует начать с простого книжного шифра.

Перед началом работы необходимо выбрать книгу и страницу, которые будут использоваться для шифрования. Это может быть, например, первая страница первой части третьего тома романа «Война и мир» Льва Николаевича Толстого. Для шифрования простого сообщения достаточно воспользоваться первыми двумя абзацами текста.

«С конца 1811 года началось усиленное вооружение и сосредоточение сил Западной Европы, и в 1812 году силы эти — миллионы людей (считая тех, которые перевозили и кормили армию) двинулись с Запада на Восток, к границам России, к которым точно так же с 1811 года стягивались силы России. 12 июня силы Западной Европы перешли границы России, и началась война, то есть совершилось противное человеческому разуму и всей человеческой природе событие. Миллионы людей совершали друг против друга такое бесчисленное количество злодеяний, обманов, измен, воровства, подделок и выпуска фальшивых ассигнаций, грабежей, поджогов и убийств, которого в целые века не соберет летопись всех судов мира и на которые в этот период времени люди, совершавшие их, не смотрели как на преступления.

Что произвело это необычайное событие? Какие были причины его? Историки с наивной уверенностью говорят, что причинами этого события были обида, нанесенная герцогу Ольденбургскому, несоблюдение континентальной системы, властолюбие Наполеона, твердость Александра, ошибки дипломатов и т. п.»

Все слова текста, напечатанного на этой странице бессмертного произведения великого русского классика, за исключением дат, следует пронумеровать. В результате текст примет следующий вид:

«С(1) конца(2) 1811 года(3) началось(4) усиленное(5) вооружение(6) и(7) сосредоточение(8) сил(9) Западной(10) Европы(11), и(12) в(13) 1812году(14)силы(15)эти(16) — миллионы(17) людей(18) (считая(19) тех(20), которые(21) перевозили(22) и(23) кормили(24) армию(25),) двинулись(26) с(27) Запада(28) на(29) Восток(30), к(31) границам(32) России(33), к(34) которым(35) точно(36) так(37) же(38) с(39) 1811 года(40) стягивались(41) силы(42) России(43). 12 июня(44) силы(45) Западной(46) Европы(47) перешли(48) границы(49) России(50), и(51) началась(52) война(53), то(54) есть(55) совершилосъ(56) противное(57) человеческому(58) разуму(59) и(60) всей(61) человеческой(62) природе(63) событие(64). Миллионы(65) людей(66) совершали(67) друг(68) против(69) друга(70) такое(71) бесчисленное(72) количество(73) злодеяний(74), обманов(75), измен(76), воровства(77), подделок(78) и(79) выпуска(80) фальшивых(81) ассигнаций(82), грабежей(83), поджогов(84) и(85) убийств(86), которого(87) в(88) целые(89) века(90) не(91) соберет(92) летопись(93) всех(94) судов(95) мира(96) и(97) на(98) которые(99) в(100) этот(101) период(102) времени(ЮЗ) люди(104), совершавшие(105) их(106), не(107) смотрели(108) как(109) на(110) преступления(111).

Что(112) произвело(113) это(114) необычайное(115) событием(116)? Какие(117) были(118) причины(119) его(120)? Историки(121) с(122) наивнойМ23) уверенностью(124) говорятМ25), что(126) причинамиМ?7) этого(128) события(129) были(130) обида(131), нанесеннаяМ32) герцогу(133) Ольденбургскому(134), несо6людение(135) контентальной(136) системы(137), властолюбие(138) Наполеона(139), твердость(140) Александра(141), ошибки(142) дипламатов(143) ит.(144) п.(145).

Алгоритм шифрования при использовании простого книжного шифра заключается в том, что цифра 1 обозначает первую букву первого слова, то есть в рассматриваемом примере букву С. Цифра 2 соответствует первой букве второго слова — букве К и так далее. Например, число 38 соответствует букве Ж, а число 81 — букве Ф.

Наблюдательный читатель заметит, что одной и той же букве соответствуют разные числа. Так, например, букве Г соответствуют числа 3,14,32 и др. В этом заключается одно из достоинств книжного шифра. Поскольку одну и ту же букву открытого текста в криптограмме можно заменить разными числами, разгадать такую криптограмму с помощью методов частотного анализа невозможно.

В качестве примера попробуем зашифровать с помощью простого книжного шифра открытый текст СЕКРЕТНОЕ ПОСЛАНИЕ. Итак, если в данном открытом тексте заменить буквы на соответствующие им числа из приведенного выше текста, то полученная криптограмма будет выглядеть так:

1.11.87.33.47.71.107.75.55. 22.134.108.93.25.91.121.120

Для того чтобы расшифровать это сообщение, получатель должен в аналогичной книге на известной ему странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы.

Усовершенствованный книжный шифр

При практическом применении рассмотренного ранее простого книжного шифра пользователь, без сомнения, столкнется с одной трудно разрешимой проблемой. Она заключается в том, что в русском алфавите есть буквы, с которых начинается лишь небольшое число слов, таких как, например, буква Ы. Найти такие слова в подавляющем числе книг просто невозможно. В то же время в русском языке практически вообще нет слов, которые начинались бы с таких букв, как Ъ или Ь. Однако незначительное усовершенствование простого книжного шифра позволяет решить эту задачу.

В усовершенствованном книжном шифре для замены каждой буквы открытого текста используются два числа, записываемые через тире. При этом первое число означает порядковый номер слова в тексте, а второе число означает номер буквы в этом слове.

Так, например, в приведенном ранее тексте первой страницы первой части третьего тома романа «Война и мир» Л. Н. Толстого число 2–4 соответствует четвертой букве второго слова, то есть букве Ц Таким же образом определяются числа для других букв. Число 46-8 соответствует в данном темпе букве Й, число 134-3 — букве Ь, число 49-7 — букве Ы и так далее.

Теперь, если в открытом тексте СЕКРЕТНОЕ ПОСЛАНИЕ заменить буквы на соответствующие им числа в соответствии с рассматриваемым алгоритмом шифрования, то полученная криптограмма будет выглядеть так:

4–7.48-2.117-1.83-2.89-5.137-4.57-7.101-3.67-4. 48-1.123-6.82-3.74-2.117-2.124-7.119-3.20-2

Расшифровка такой криптограммы для получателя сообщения не представляет труда. Достаточно в аналогичной книге на определенной странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы. В то же время несанкционированный пользователь разгадать подобную шифрограмму не сможет.

5.6. Тайны решеток и таблиц

Уже в древние века наши предки для создания шифрованных сообщений использовали специальные системы шифрования, основу которых составляли так называемые решетки, в отдельные клетки которых в определенном порядке записывались буквы алфавита.

Не менее известны и шифры, при применении которых используются специальные таблицы, ячейки которых также заполняются буквами алфавита При этом шифровальные таблицы с одинаковым количеством строк и столбцов получили название квадратов.

Шифры с использованием всевозможных шифровальных таблиц и решеток постоянно совершенствовались и усложнялись. В то же время эти шифры благодаря простоте их составления и применения может использовать даже неподготовленный пользователь.

В зависимости от используемых алгоритмов данные системы шифрования можно разделить на шифры замены и шифры перестановки. При этом среди шифров замены на основе таблиц следует отметить, например, квадрат Полибия, так называемый шифр «Большой крест» и др.

Простая шифровальная таблица

Данный шифр является одним из самых простых. Его основу составляет таблица, ячейки которой заполнены буквами алфавита. Для русского алфавита такая шифровальная таблица может состоять из шести столбцов по пять строк в каждом, которая будет выглядеть следующим образом:

Теперь эту таблицу следует дополнить еще одним столбцом, который заполнен буквами, и строкой, заполненной цифрами. При этом буквы и цифры могут быть абсолютно любыми. Для начала заполним ячейки дополнительной строки цифрами от 1 до 6, а ячейки дополнительного столбца заполним буквами от А до Д.

В итоге шифровальная таблица примет следующий вид:

Правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так, например, в данной таблице ячейка с буквой С находится на пересечении строки В и столбца 5. Поэтому при шифровании открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ с помощью рассматриваемого шифра буква С должна быть заменена на сочетание или группу В5. Таким же образом букву Е открытого текста надо заменить на А6, букву К — на Б4 и так далее. В результате шифрования криптограмма примет следующий вид:

В5.А6.Б4.В4.А6.В6.В1 В2.А6. В5.В2.В2.А2.Д1.А6.В1.БЗ.А6.

Для расшифровки такой криптограммы следует использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая комбинация буквы и цифры шифрограммы должна быть заменена на букву, расположенную в соответствующей ячейке на пересечении строки и столбца, обозначенных этой буквой и этой цифрой. В рассматриваемом примере вместо комбинации В5 следует записать букву С, вместо А6 — букву Е и так далее, пока не будет расшифрован весь текст.

В одном из вариантов такого шифра для обозначения строк также можно использовать цифры. При этом шифровальная таблица будет выглядеть вот так:

После шифрования открытого текста с помощью приведенного выше алгоритма криптограмма будет состоять из нескольких пар или групп цифр. При этом в каждой группе первая цифра обозначает строку, а вторая цифра — столбец, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так например, в результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма примет следующий вид:

35.16.24.34.16.36.31.32.16. 35.32.32.12.51.16.31.23.16.

Расшифровка такой криптограммы заключается в замене пар или групп цифр буквами, находящимися в тех ячейках таблицы, строки и столбцы для которых обозначены соответствующими цифрами.

Таблица с паролем

В приведенных ранее примерах шифров буквы в ячейки шифровальных таблиц вписывались в том порядке, в каком они расположены в алфавите. Естественно, стойкость таких шифров оставляет желать лучшего. Поэтому чаще всего при применении различных шифровальных систем, основанных на использовании таблиц, буквы алфавита в ячейки таких таблиц вписываются в случайном порядке или в соответствии с определенным правилом. Главное, чтобы порядок заполнения ячеек был известен получателю.

Наиболее удобным вариантом будет конечно же тот, когда ячейки заполнены в абсолютно произвольном порядке, а получатель уже имеет готовую таблицу с записанными в ячейки буквами. Однако в этом случае велик риск того, что такая шифровальная таблица может оказаться в руках незаконного пользователя со всеми вытекающими последствиями. Поэтому желательно, чтобы отправитель и получатель сообщения не хранили у себя шифровальную таблицу, а лишь знали, по какому правилу она составляется. При необходимости на основании такого правила всегда можно составить шифровальную таблицу, с ее помощью зашифровать или расшифровать сообщение, а затем эту таблицу уничтожить.

Одним из способов заполнения таблиц является использование паролей. Для составления такой таблицы сначала необходимо выбрать пароль или кодовое слово. При этом желательно, чтобы в пароле не было повторяющихся букв. Конечно же данная рекомендация не является обязательной. После этого буквы пароля вписываются в первые ячейки таблицы, а остальные ячейки заполняются оставшимися, не использованными в пароле, буквами алфавита.

Так, например, если в качестве пароля выбрано слово ПАРОДИЯ, то шифровальная таблица примет следующий вид;

Если теперь эту таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться одним из рассмотренных ранее алгоритмов шифрования.

При использовании этого шифра каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу таблицы, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В6.Б5.В2.АЗ.Б5.Г1.В5.А4.Б5. В6.А4.А4.Б2.Д2.Б5.В5.А6.Б5.

Таким же образом можно зашифровать сообщение с помощью таблицы, в которой для обозначения столбцов и строк используются только цифры.

В этом случае после шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма будет выглядеть так:

36.25.32.13.25.41.35.14.25. 36.14.14.22.52.25.35.16.25.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы такие буквы следует пропустить.

Так, например, если в качестве пароля выбрано слово ПЕРЕПРАВА, то повторяющиеся буквы Е, П, Р и В не записываются в ячейки, а пропускаются. При этом шифровальная таблица примет следующий вид:

Если теперь данную таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться уже упоминавшимся алгоритмом шифрования.

Напомним, что при использовании этого шифра правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста. В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В5.А2.Б6.АЗ.А2.В6.ВЗ.В4.А2. В5.В4.В4.А6.Д1.А2.ВЗ.Б5.А2.

И в этой таблице для обозначения строк можно использовать цифры. При этом порядок применения алгоритма шифрования не отличается от рассмотренных ранее шифров.

Для того чтобы усложнить незаконному пользователю задачу взлома шифра, вместо повторяющихся в пароле букв в ячейки можно вписывать оставшиеся буквы алфавита. Так, например, при использовании в качестве пароля слова ПЕРЕПРАВА повторяющиеся буквы Е, П, Р и В не записываются в ячейки. Вместо них в соответствующие ячейки вставляются не вошедшие в пароль следующие буквы алфавита Для рассматриваемого пароля вместо второй буквы Е следует записать букву Б, вместо второй буквы П — букву Г, вместо второй буквы Р — букву Д и так далее. При этом шифровальная таблица примет следующий вид:

Такую таблицу можно использовать для шифрования сообщений в соответствии как с рассмотренными ранее алгоритмами шифрования, так и с другими.

Следует отметить, что паролем может служить не только отдельное слово, но и целая фраза. Эго может быть известная поговорка или пословица, цитата или строка из стихотворения. При этом правила заполнения ячеек шифровальной таблицы буквами алфавита остаются такими же, как и для уже упоминавшихся таблиц с простым паролем.

Так, например, при использовании в качестве пароля фразы ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ шифровальная таблица может выглядеть следующим образом:

Такую таблицу также можно использовать для шифрования сообщений в соответствии как со всеми рассмотренными ранее алгоритмами шифрования, так и с другими.

Квадрат Полибия

Одну из первых систем шифрования, в которой использовалась таблица, описал древнегреческий историк Полибий. Точно неизвестно, является ли талантливый писатель автором этого шифра. Тем не менее специалисты называют этот шифр «квадратом Полибия». Еще до наступления нашей эры этот шифр широко применялся как греками, так и римлянами.

При использовании данного шифра составляется таблица, которая, например, для английского алфавита состоит из пяти столбцов по пять строк в каждом. В каждую клетку этой таблицы в произвольном порядке вписывается одна из букв алфавита. Необходимо отметить, что для русского алфавита, содержащего большее количество букв, шифровальная таблица должна содержать не менее 30 клеток. Эго может быть, например, таблица из шести столбцов по пять строк в каждом.

Алгоритм шифрования заключается в том, что при преобразовании открытого текста в криптограмму необходимо найти в таблице ячейку с нужной буквой и вставить в шифрованный текст букву, располагающуюся в нижней от нее ячейке в том же столбце. Если же буква открытого текста оказывается в ячейке нижней строки, то в шифрограмму следует записать букву из верхней ячейки того же столбца.

В качестве при мера зашифруем с помощью шифра «квадрат Полибия» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Перед началом работы необходимо составить шифровальную таблицу, которая может выглядеть, например, вот так:

Теперь следует найти клетку с первой буквой открытого текста Эго буква С, ячейка с которой расположена в третьей строке третьего столбца. В соответствии с алгоритмом шифрования вместо этой буквы в криптограмму необходимо записать букву, расположенную в нижней от нее ячейке в том же столбце, то есть вместо буквы С — букву К. Таким же образом букву Е открытого текста надо заменить на букву У, букву К на букву Ц и так далее. Не следует забывать о том, что в случае если буква открытого текста окажется в ячейке нижней строки, то в шифрограмму следует записать букву из самой верхней ячейки того же столбца. Например, буква Р должна быть заменена в криптограмме на букву Ю.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕс помощью рассматриваемого шифра криптограмма примет следующий вид:

КУЦЮУПВНУ КННИГУВМУ

Для расшифровки получатель сообщения должен использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая буква шифрограммы должна быть заменена на букву, расположенную в верхней от нее ячейке в том же столбце.

В рассматриваемом примере вместо буквы К следует записать букву С, вместо буквы У — букву Е и так далее, пока не будет расшифрован весь текст. Если же буква из криптограммы в таблице занимает верхнюю ячейку, то ее следует заменить на букву, находящуюся в самой нижней ячейке того же столбца.

Шифр «Большой крест»

Первые упоминания о шифре, в некоторых источниках называемом «Большой крест», относятся к XVIII столетию. Необходимо отметить, что в отдельных зарубежных изданиях автору встречались варианты этого шифра с весьма экзотическими названиями. Например, название одного из вариантов можно перевести на русский язык как шифр «Загончики для поросят».

Шифр «Большой крест» прост и в то же время очень эффективен. Неподготовленный незаконный пользователь, желающий прочитать сообщение, зашифрованное с помощью данного шифра замены, вряд ли сможет сразу догадаться, как его взломать. В связи с ограниченным объемом данной книги далее будут рассмотрены лишь некоторые варианты шифра «Большой крест».

Практическое использование данного шифра следует начать с составления специальной шифровальной таблицы, которая будет выглядеть как несколько решеток. В одном из вариантов такая таблица может иметь вид, показанный на рис. 5.1.

Рис. 5.1 Шифровальная таблица для шифра «Большой крест»

В качестве примера зашифруем с помощью шифра «Большой крест» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Если заменить буквы открытого текста соответствующими им символами ячеек решетки, то получится промежуточный результат, показанный на рис. 5.2.

В окончательном виде криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ будет выглядеть так, как показано на рис. 5.3.

Рис. 5.2 Промежуточный результат шифрования с помощью шифра «Большой крест»

Рис. 5.3 Криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ полученная в результате использования шифра «Большой крест»

Если с помощью рассматриваемого шифра зашифровать открытый текст ИЛЛЮЗИЯ, то криптограмма примет вид показанный на рис. 5.4.

Рис. 5.4 Криптограмма для открытого текста ИЛЛЮЗИЯ, полученная в результате использования шифра «Большой крест»

Для того чтобы расшифровать приведенные криптограммы, достаточно составить аналогичную шифровальную таблицу и заменить символы на соответствующие им буквы.

Необходимо отметить, что комбинаций расположения букв в ячейках решеток может быть довольно много. Поэтому законный пользователь для шифрования сообщений при желании может придумать свой, оригинальный вариант шифра «Большой крест».

5.7. Перестановки в таблицах

В шифрах, основу которых составляют таблицы, применяются самые разнообразные алгоритмы шифрования. Ранее были рассмотрены несколько простых систем шифрования, в которых используются специальные таблицы, ячейки которых заполняются буквами алфавита.

При этом составление криптограммы заключается в замене букв открытого текста в соответствии с определенными правилами.

В то же время существует множество шифров, при работе с которыми также составляются таблицы, однако ячейки этих таблиц заполняются не всеми буквами алфавита, а только буквами открытого текста. Алгоритм шифрования при использовании таких шифров заключается в том, что строки и столбцы в таблице с открытым текстом переставляются или перемешаются в соответствии с определенным правилом.

Простая перестановка

Одним из шифров, основанных на перестановке строк и столбцов в таблице с открытым текстом, является шифр простой перестановки. Создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно. После заполнения таблицы буквы в криптограмму выписываются по столбцам, сначала из первого столбца, затем из второго и так далее.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. При выборе таблицы, состоящей из пяти строк и шести столбцов, ее ячейки будут заполнены следующим образом:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первого столбца, затем из ячеек второго столбца и так далее.

В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

МСИТЗ ЕТЗЬМ СРМНО ТЕЕЕЖ ОЧНВН ВИИОО

Если записать эту криптограмму без пробелов, то она примет следующий вид:

МСИТЗЕТЗЫИСРМНОТЕЕЕЖОЧНВНВИИОО

Для расшифровки такого шифрованного сообщения достаточно в таблицу аналогичных размеров по столбцам вписать буквы криптограммы, а затем по строкам прочитать открытый текст. Естественно, для этого получатель сообщения должен знать размер таблицы.

Перестановка с паролем

Не менее интересен более сложный способ шифрования, который можно назвать перестановкой с паролем. При использовании этого шифра столбцы или строки в таблице, заполненной буквами открытого текста, перемещаются на определенное количество позиций по определенному правилу. Порядок перемещения столбцов или строк в таблице должен быть известен получателю сообщения.

Как и в рассмотренном ранее шифре простой перестановки, создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно.

Если пользователь решил произвести перестановку столбцов, то к этой таблице следует добавить еще две строки. В ячейки первой добавленной строки необходимо вписать буквы пароля. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

После этого необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьей строки, затем из ячеек четвертой строки и так далее.

ТОСМЕВ ЕЧРСТИ ЕНМИЗИ ЕВНТЬО ЖНОЗМО

Для того чтобы расшифровать эту шифрограмму, получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во второй строке которой записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по строкам буквами криптограммы. Если теперь переставить столбцы таблицы так, чтобы буквы в верхней строчке образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

Таким же образом в таблице с открытым текстом можно произвести перестановку строк. В этом случае к первоначальной таблице следует добавить еще два столбца. При этом в ячейки первого добавленного столбца необходимо вписать буквы пароля. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ВЕСНА, то шифровальная таблица для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

После этого необходимо переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. В результате такой перестановки таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьего столбца, затем из ячеек четвертого столбца и так далее.

В окончательном виде шифрограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЗМСТИ МЕТЬЗ ОСРНМ ЖТЕЕЕ НОЧВН ОВИОИ

Для расшифровки этой криптограммы получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во втором столбце шторой записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по столбцам буквами криптограммы. Если теперь переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы номера таким буквам присваиваются слева направо.

Двойная перестановка

Следует признать, что рассмотренные ранее системы шифрования, в которых применяется перестановка столбцов и строк шифровальной таблицы, ячейки которой заполнены буквами открытого текста, имеют сравнительно низкую стойкость. Для специалистов взлом таких шифров не представляет особого труда. В то же время неподготовленный незаконный пользователь на разгадку подобного шифра будет вынужден затратить немало времени. Задача взлома шифра значительно усложнится, если отправитель сообщения воспользуется так называемым шифром двойной перестановки.

При использовании шифра двойной перестановки в таблице, заполненной буквами открытого текста, на определенное количество позиций по определенному правилу перемещаются как столбцы, так и строки.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. Если пользователь решил воспользоваться шифром двойной перестановки, то к уже знакомой шифровальной таблице, состоящей из пяти строк и шести столбцов, следует добавить еще две строки и два столбца. При этом ячейки таблицы будут заполнены следующим образом:

В ячейки первой добавленной строки необходимо вписать буквы пароля для перестановки столбцов. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки столбцов выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

В ячейки первого добавленного столбца необходимо вписать буквы пароля для перестановки строк. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки строк выбрать, например, слово ВЕСНА, то шифровальная таблица примет следующий вид:

Для создания криптограммы сначала необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

После этого следует переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. После выполнения такой перестановки таблица будет выглядеть вот так:

Теперь дпя создания шифрограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки ит. д. В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЖНОЗМО ТОСМЕВ ЕЧРСТИ ЕВНТЬО ЕНМИЗИ

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен знать пароли для перемещения столбцов и строк Затем необходимо составить аналогичную шифровальную таблицу. Во второй строке этой таблицы записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Остальные ячейки следует заполнить по строкам буквами криптограммы. Теперь необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. После этого достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк и в строках таблицы получатель сообщения сможет прочитать открытый текст.

В процессе шифрования буквы из ячеек шифровальной таблицы можно выписать и по столбцам, сначала из ячеек первого столбца, затем из ячеек второго столбца и так далее. В этом случае криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

ЖТЕЕЕ НОЧВН ОСРНМ ЗМСТИ МЕТЬЗ ОВИОИ

Однако в этом случае порядок действий при дешифровании незначительно изменится. При составлении таблицы получатель сообщения, как и в рассмотренном ранее примере, во второй строке должен записать цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Однако остальные ячейки следует заполнить буквами криптограммы не по строкам, а по столбцам.

После этого, как и в рассмотренном ранее примере, необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. Теперь достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк, и в строках таблицы получатель сообщения сможет прочитать открытый текст.

5.8. Магические квадраты

В Средние века широкое распространение получили шифры, основу которых составляли так называемые магические квадраты.

В математике магическими квадратами называются таблицы с одинаковым количеством строк и столбцов. В каждую ячейку такой таблицы вписывается какое-либо число, при этом сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число.

Необходимо отметить, что для шифрования проще всего использовать магические квадраты, в ячейки которых записываются числа по порядку без повторов, начиная от цифры 1 и до числа, которое определяется количеством ячеек в данном квадрате. При этом не следует забывать о том, что для шифрования длинных сообщений потребуются таблицы большего размера. Так, например, для шифрования открытого текста, состоящего из 16 знаков, достаточно воспользоваться магическим квадратом размером 4×4, а для шифрования текста, содержащего 64 знака, потребуется таблица размером 8×8.

При использовании шифров, основанных на магических квадратах, алгоритм шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата по определенному правилу вписываются буквы и знаки открытого текста После того как все ячейки будут заполнены, текст криптограммы выписывается из таблицы по строкам или по столбцам.

Простейший магический квадрат

Как известно, чем меньше столбцов и строк в квадратной таблице, тем меньше вариантов построения на ее основе магического квадрата Так, например, для таблицы, состоящей из трех столбцов и трех строк, известен всего лишь один вариант заполнения ячеек цифрами от 1 до 9, в результате которого получится магический квадрат. Такая таблица будет выглядеть так:

Нетрудно подсчитать, что сумма цифр в каждом столбце, в каждой строке и в каждой большой диагонали составляет одно и то же число и равна 15.

При использовании шифров, основанных на магических квадратах, один из простейших алгоритмов шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата вписываются по порядку буквы открытого текста. Так, например, вместо цифры 1 в соответствующую ей ячейку следует записать первую букву сообщения, вместо цифры 2 — вторую букву, вместо цифры 3 — третью букву и так далее.

В качестве примера зашифруем с помощью этого магического квадрата открытый текст РАЗВЕДЧИК При этом в ячейку с цифрой 1 следует записать букву Р, в ячейку с цифрой 2 — букву А, в ячейку с цифрой 3 — букву 3 и так до конца сообщения. В результате таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста РАЗВЕДЧИК будет выглядеть так:

ИРД ЗЕЧ ВКА

Получив такую шифрограмму, получатель для расшифровки сообщения должен сначала заполнить таблицу буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

Необходимо отметить, что утверждение о существовании лишь одного магического квадрата размером 3×3 для цифр от 1 до 9 не касается случаев, когда другие магические квадраты могут быть образованы из первоначального с помощью поворота таблицы или отражения строк и столбцов.

Один из таких производных квадратов может выглядеть следующим образом:

Такой магический квадрат также с успехом можно использовать для шифрования коротких сообщений в соответствии с приведенным выше алгоритмом.

Индийский квадрат

В одном из древних индийских храмов исследователи обнаружили квадратную таблицу, которая при более подробном изучении оказалась одним из самых первых известных магических квадратов. По мнению некоторых историков, эта таблица была создана в XII веке.

Ячейки данной таблицы, состоящей из четырех столбцов и четырех строк, заполнены числами от 1 до 16 так, что сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число, а именно 34. Более того, сумма чисел в четырех ячейках, образующих квадратные таблицы внутри данного магического квадрата, также составляет 34.

Порядок заполнения ячеек в этой таблице выглядит следующим образом:

Естественно, что такой магический квадрат также можно использовать для шифровки короткого сообщения, содержащего до шестнадцати знаков.

В качестве примера зашифруем, например, открытый текст СЕКРЕТНАЯ ВСТРЕЧА. Для шифрования данного сообщения с использованием рассмотренного ранее алгоритма необходимо сначала вставить в ячейки таблицы вместо цифр буквы открытого текста. При этом вместо цифры 1 в соответствующую ячейку следует вставить первую букву открытого текста, в рассматриваемом примере это будет буква С. Вместо цифры 2 в соответствующую ячейку следует вставить вторую букву открытого текста, то есть букву Е, и так далее.

В результате такой замены шифровальная таблица примет следующий вид:

В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

НТСЕ ЕРАС АКВЕ ЯТЧР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

По утверждению некоторых источников, классических магических квадратов размером 4×4 существует всего 12. При этом другие магические квадраты тех же размеров могут быть образованы из первоначального, например с помощью поворота таблицы или отражения строк и столбцов. Общее число таких производных магических квадратов разными специалистами оценивается от нескольких сотен до нескольких тысяч. С учетом того, что любой из упомянутых магических квадратов может быть использован для шифрования сообщения, задача взлома шифра для незаконного пользователя с помощью подбора необходимой таблицы вручную становится практически невыполнимой.

Квадрат Эйлера

Известный математик, астролог и криптограф Леонард Эйлер, долгое время работавший в России в XVIII веке, является автором известной таблицы, состоящей из восьми столбцов и восьми строк.

Все клетки так называемого квадрата Эйлера заполнены числами от 1 до 64 так, что сумма всех чисел, расположенных в одном столбце и в одной строке, составляет одно и то же число, а именно 260. Более того, если данную таблицу разделить на четыре квадратные таблицы, то и в каждой из них сумма чисел в ячейках одного столбца и одной строки также будет одинакова и составит 130. Таким же свойством обладает и квадрат размером 4×4, составленный из ячеек, расположенных в центральной части большой таблицы.

Порядок заполнения ячеек в квадрате Эйлера выглядит следующим образом:

Нетрудно заметить, что с математической точки зрения данная таблица не является классическим магическим квадратом, поскольку суммы чисел в ячейках, образующих диагонали, не равны между собой. В то же время квадрат Эйлера можно использовать для шифрования сравнительно длинных сообщений, используя алгоритм шифрования, рассмотренный ранее для классических магических квадратов.

Магический квадрат 9×9

Как отмечалось ранее, для шифрования длинных сообщений необходимо использовать таблицы большего размера. При этом не следует забывать о том, что чем больше столбцов и строк в квадратной таблице, тем больше вариантов построения на ее основе магического квадрата. Данный факт значительно усложняет незаконному пользователю задачу расшифровки сообщений, зашифрованных, например, с помощью магического квадрата размером 4×4.

Естественно, применение магических квадратов, например, размером 9×9 обеспечивает еще более высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано тем, кому оно не предназначено.

Один из вариантов такого квадрата имеет следующий вид:

Как и упоминавшийся квадрат Эйлера, данный магический квадрат также можно использовать для шифрования длинных сообщений, используя рассмотренный ранее алгоритм шифрования для классических магических квадратов. При этом открытый текст может содержать до 81 знака.

5.9. Трафарет в системах шифрования

Для создания шифрованных сообщений можно использовать специальные трафареты, которые представляют собой, например, лист бумаги с вырезанными в произвольном порядке отверстиями. Необходимо отметить, что в настоящее время известно множество систем шифрования, в которых применяются различные способы создания и использования таких трафаретов. Естественно, при применении таких шифров получатель криптограммы должен не только иметь точно такой же трафарет, но и хорошо знать правила работы с ним.

Один из вариантов простого шифра с использованием трафарета применял, например, великий русский писатель А. С. Грибоедов в начале XIX века. На лист бумаги он с помощью трафарета наносил текст сообщения, а затем уже без трафарета дополнял текст так, чтобы получилось вполне невинное письмо.

Трафаретные шифры неоднократно упоминаются и в произведениях авторов детективных романов. Среди более сложных шифров с трафаретами следует отметить, например, так называемую решетку Кардано.

Простой шифр с трафаретом

При использовании такого способа шифрования сначала необходимо сделать трафарет из листа бумаги с вырезанными в нем отверстиями. Для этого удобно воспользоваться листом бумаги в клеточку, в котором отдельные клетки следует вырезать в произвольном порядке.

Так, например, трафарет для шифрования сообщений может выглядеть так, как показано на рис. 5.5.

Рис. 5.5 Один из вариантов трафарета для шифрования сообщений

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью данного трафарета открытый текст СЕКРЕТНОЕ ПИСЬМО. Для этого сначала необходимо наложить трафарет на чистый лист бумаги и в вырезанных прямоугольниках вписать буквы открытого текста.

В результате на листе получится следующая надпись:

Теперь для создания криптограммы достаточно убрать трафарет и между буквами открытого текста вписать любые другие буквы в произвольном порядке. В этом случае криптограмма может принять следующий вид:

Для того чтобы запутать незаконного пользователя, буквы можно вписать так, чтобы получился какой-либо вполне обычный текст.

При расшифровке такой криптограммы получателю сообщения достаточно наложить аналогичный трафарет на лист с текстом и в вырезанных ячейках прочитать открытый текст.

Необходимо отметить, что при использовании данного шифра для шифровки сравнительно коротких сообщений при создании трафарета необходимо обратить внимание на то, чтобы количество вырезанных клеточек было не меньше, чем количество букв в открытом тексте. Для шифровки длинных сообщений можно сделать трафарет с большим количеством вырезанных ячеек или же один и тот же трафарет использовать несколько раз.

Решетка Кардано

Более сложной системой шифрования, в которой также используется трафарет определенной формы, является шифр, называемый решеткой Кардано. Название этого шифра произошло от имени его автора, итальянского математика и философа Джероламо Кардано. Именно он в далеком 1566 году водной из своих работ опубликовал описание рассматриваемого шифра.

Основу простейшей решетки Кардано составляет трафарет, выполненный в форме квадратной таблицы. При этом ячейки в данном трафарете вырезаются так, чтобы после поворота трафарета вокруг центральной оси буквы, записанные в ячейках на подложенном листе бумага, не перекрывались. Другими словами, при четырех поворотах трафарета на 90? ячейки, перекрыв все клетки таблицы, ни разу не должны оказаться в одном и том же месте.

Рис. 5.8 Решетка Кардано размером 4×4

Так, например, вариант такого трафарета размером 4×4 имеет вид, изображенный на рис. 5.6.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью решетки Кардано открытый текст СЕКРЕТНАЯ ВСТРЕЧА Шифрование данного сообщения необходимо начать с заполнения ячеек таблицы буквами открытого текста Для этого наложим трафарет на лист с таблицей и в вырезанные ячейки впишем первые буквы открытого текста. В рассматриваемом примере это первые четыре буквы, а именно буквы С, Е, К и Р.

В результате надпись на листе будет выглядеть так:

После этого повернем трафарет по часовой стрелке на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста В рассматриваемом примере это буквы Е, Т, Н и А

Теперь повернем трафарет по часовой стрелке еще на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста а именно буквы Е, П, И и С.

Следующий поворот трафарета также следует провести по часовой стрелке еще на 90?, а свободные ячейки заполнить оставшимися четырьмя буквами открытого текста

После заполнения всех свободных ячеек и снятия трафарета на листе бумаги останется шифровальная таблица которая имеет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее. В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

ЯСЕР ЕВЕТ ЧНКС ААТР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы. Затем необходимо наложить на заполненную таблицу трафарет и, поворачивая его по часовой стрелке на 90?, последовательно выписать из открывающихся ячеек буквы открытого текста.

Рис. 5.7 Решетка Кардано размером 6×6

Если пользователю потребуется зашифровать открытый текст, содержащий большое количество знаков, то решетку Кардано размером 4×4 можно использовать неоднократно.

В то же время для шифрования длинных сообщений любой желающий может составить и использовать решетку Кардано практически любых размеров.

Один из вариантов решетки Кардано размером 6×6 имеет вид, изображенный на рис. 5.7.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать. Порядок пользования этим трафаретом аналогичен ранее рассмотренному.

Остается добавить, что применение решеток Кардано обеспечивает сравнительно высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано неподготовленным незаконным пользователем. Однако для специалиста взлом такого шифра не представляет особых трудностей.

5.10. Биграммные шифры

Одной из особенностей рассмотренных ранее систем шифрования является то, что в них каждая буква открытого текста шифруется отдельно. Однако еще в Средние века некоторые ученые предложили шифры с использованием алгоритмов, обеспечивающих одновременное шифрование сразу двух букв сообщения. Такие шифры стали называться биграммными.

Одно из первых описаний биграммного шифра было опубликовано немецким ученым И. Тритемиусом в начале XVI века Однако некоторые специалисты считают, что первое заслуживающее внимания описание биграммного шифра привел итальянец Д. Порта в 1563 году в книге «О тайной переписке».

Необходимо отметить, что биграммные шифры, несмотря на более высокую степень защищенности, по сравнению с другими использовавшимися в то время системами шифрования, в течение примерно 300 лет почти не применялись. И лишь в XIX веке одновременно в нескольких европейских странах началась активная работа над созданием оригинальных биграммных шифров. Так, например, в России над своим вариантом биграммного шифра работал талантливый криптограф и изобретатель П. Ф. Шиллинг, а в Британии — Ч. Ветстоун.

Название одного из биграммных шифров, придуманного в XIX веке, связано с именем министра почт Британской империи барона Л. Плейфера (L Playfair). Шифр «Playfair» был настолько удачным, что в различных версиях применялся англичанами и во время Первой мировой войны уже в XX столетии.

При использовании шифра «Playfair» алгоритм шифрования заключается в том, что открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы. При этом в процессе шифрования необходимо использовать таблицу, заполненную буквами соответствующего алфавита.

В оригинальном шифре «Playfair» для английского алфавита применяется таблица размером 5×5 с паролем Playfair. Для русского алфавита можно использовать, например, уже рассмотренную ранее таблицу с паролем ПАРОДИЯ:

В качестве примера зашифруем с помощью шифра «Playfair» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв, которые часто называются группами. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующ ий вид;

СЕ КР ЕТ НО ЕС ОО БЩ ЕН ИЕ

Необходимо отметить, что в соответствии с алгоритмом шифрования пара или группа букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У.

В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

С учетом данных требований в рассматриваемом примере открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ, разделенный на пары букв, будет выглядеть вот так:

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару букв следует зашифровать отдельно с помощью составленной ранее шифровальной таблицы, ячейки которой должны быть заполнены буквами алфавита по определенному правилу. В нашем примере это приведенная выше таблица с паролем ПАРОДИЯ.

Сначала в таблице надо найти каждую из двух букв, входящих в состав подлежащей шифрованию группы. Затем следует мысленно построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы НЖ, вместо букв КР — буквы ЛА, вместо букв ЕТ — буквы ЯЦ и так далее.

В случае если обе буквы какой-либо группы открытого текста находятся в одном столбце таблицы, то в криптограмму записываются буквы, находящиеся под ними, то есть в соответствующих ячейках следующей строки.

Так, в рассматриваемом примере при шифровании группы ОХ открытого текста в криптограмму записывается пара ГЫ Если же при этом одна из пары букв открытого текста окажется в нижней строке столбца, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в верхней строке этого столбца.

В случае, если обе буквы какой-либо группы открытого текста находятся в одной строке таблицы, то в криптограмму записываются буквы, находящиеся справа от них, то есть в соответствующих ячейках следующего столбца.

Так, например, при шифровании группы ТХ открытого текста в криптограмму записывается пара УЦ. Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

НЖ ЛА ЯЦ МД ЖН ГЫ АГ ЭБ СД ГЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известного ему правила или пароля составить таблицу, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы букв открытого текста.

Шифр «Двойной квадрат»

Помимо шифра «Playfair», в том же XIX веке был изобретен биграммный шифр, получивший название «Двойной квадрат». Однако, в отличие от шифра «Playfair», при применении шифра «Двойной квадрат» в процессе шифрования используется не одна, а две таблицы, ячейки которых заполнены буквами алфавита.

В то же время алгоритмы шифрования указанных шифров очень похожи: открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы.

Перед началом шифрования открытого текста с помощью шифра «Двойной квадрат» необходимо составить две таблицы, заполненные буквами алфавита Для русского алфавита можно использовать, например, уже рассмотренные ранее таблицы с паролем ПАРОДИЯ и с паролем ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ, которые следует расположить рядом:

В качестве примера зашифруем с помощью шифра «Двойной квадрат» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

СЕ КР ЕТ НО ЕС 00 БЩ ЕН ИЕ

В соответствии с алгоритмом шифрования пара букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У. В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару или группу букв следует зашифровать отдельно. Для этого сначала надо найти эти две буквы в таблицах, при этом первая буква биграммы должна находиться в левой таблице, а вторая — в правой. После этого необходимо в двух таблицах построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста. Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке, но в другой таблице.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы ДЖ, вместо букв КР — буквы ЖА, вместо букв ЕГ — буквы БН и так далее.

При использовании данного шифра возможна ситуация, когда обе буквы какой-либо группы открытого текста окажутся в одной строке таблиц В этом случае в криптограмму вместо первой буквы биграммы открытого текста записывается буква, находящаяся в том же столбце той же строки второй таблицы. Вместо второй буквы биграммы открытого текста в криптограмму записывается буква, находящаяся в том же столбце той же строки первой таблицы.

Так, в рассматриваемом примере при шифровании группы ЕС открытого текста в криптограмму записывается пара БЖ.

Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

ДЖ ЖА БН ЮЕ БЖ ЗХ АГ ШБ ДД СЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известных ему правил или паролей составить две таблицы, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы открытого текста. При этом первая буква биграммы шифрованного текста должна находиться в правой таблице, а вторая — в левой.

значение и расшифровка цифр. Как расшифровать секретный код

Древние жрецы были правы, утверждая, что наука чисел и искусство силы духа являются магическими ключами, открывающими все двери вселенной. Это дает поразительную силу власти над собой. Наука о числах, нумерология, помогает познать себя с магической стороны цифр. Циферки все о нас объяснят и «дадут» совет на будущее. Мистика? Не совсем. Это наука, наука цифр, наряду с астрологией.

Наука простая, на уровне арифметики и безумно увлекательная. Умение читать язык цифр сделают человека чуточку волшебником, предсказывающим судьбу, что гарантирует популярность в любой компании.

Так называемая таблица Пифагора, построение которой даёт полную картину о человеке, является более универсальным инструментом.

Как расшифровать свою судьбу

Необходимо выполнить ряд несложных математических действий.

Первое : записать в строку свою дату рождения.

15 5 1967 – теперь с этими цифрами будем работать. Нули в дате рождения не вносим в строку.

Делаем четыре расчета

Расчет номер один — это важное основное число. Необходимо сложить все числа в нашей дате:

1+5+5+1+9+6+7 =34.

Теперь под цифрой 1 в строке 15 5 1967 запишите эту сумму.

Расчет номер два :

сумму в первом расчете тоже надо сложить, т.е сумму 34 складываем между собой:

запишите ее под второй цифрой нашей даты.

Расчет номер три :

Из основного числа 34 отнимает удвоенную первую цифру нашей даты рождения т.е 2.

Ее тоже пишем в нижней строке под третьей цифрой.

Расчет номер четыре :

Цифры расчета номер три надо сложить:

Теперь получили базовые цифры для таблицы Пифагора:

Первая строчка — это наша дата рождения: 15 5 1967

Вторая строчка четыре наших расчета: 34 7 32 5

Квадрат Пифагора имеет девять ячеек. Чтобы построить наш квадрат, нам необходимо внести в каждую ячейку квадрата число тех цифр, которые мы видим в двух наших строчках.

Например, в ячейку 1 вносим единицы, на самом деле их две единицы, но записать надо не два, а 11, затем в ячейку под номером 2, записываем, сколько двоек в наших строчках. В нашем случае, она одна, вот и пишем двойку в единственном числе. И так заполняем все девять ячеек.

Квадрат Пифагора для дня рождения 15 5 1967 будет выглядеть так:

Не всегда все ячейки бывают заполненными. Иногда, каких — то цифр нет в нашей матрице. В данном случае отсутствуют восьмерки. Согласно учению Пифагора пустые ячейки знаменуют отсутствие какого-то качества, которое нужно развивать, чтобы достичь духовной чистоты. Чем больше пустых клеток, тем больше человеку предстоит работа над собой, личность считается дисгармоничной.

Каждая ячейка квадрата описывает человека и силу его качеств.

Ячейка 1- Солнце (Сила характера, волевые черты)

Творческий потенциал, индивидуальность, способность жизненного горения. Показывает способность принимать решения и в одиночку их решать. Это лидерские качества. Если единиц в ячейке одна или две, то этот человек имеет покладистый характер, слабоват, нуждается в похвале и эгоист

111-спокойный по характеру, но в экстремальной ситуации проявится сильная воля.

1111- властный, сильный человек.

Недостатки: желание выделиться, эгоцентризм, позерство.

Ячейка 2- Луна (Количество энергии)

Душа человека, ее чувствительность, готовность к дружбе и взаимопониманию. Гибкость в отношениях, дипломатичность. Дар интуиции, умение предсказывать будущее.

Если имеем 2 или 22- мало энергии, не выносит конфликты, потому что сильно устает.

222 или 2222 — супер энергичен, деятелен, имеет экстрасенсорные возможности.

Недостатки: двойственность характера, его неустойчивость, капризность.

Ячейка 3- Марс (Интересы личности)

Волевые качества, агрессивность, движение к цели.

Марсу свойственно стремление к творчеству, тройка-число творца. Оптимизм и амбиции.

Люди имеют успех в коллективе, обществе, постигают вершины славы.

3 или 33 – прилежен, аккуратен, хорошо учится.

333 – педант, много интересов, но всего понемногу.

3333- все критикует и легко раздражается, нетерпим, когда нарушают его порядок.

Недостатки: грубость, переходящая в хамство, злоба и резкость.

Ячейка 4- Меркурий (Здоровье личности)

Любит порядок, размеренность, вплоть до педантичности. Преобладание четверок говорит об упорстве и надежности. Это стабильные люди, по натуре исполнители.

Имея в квадрате 4 или 44 – можно предположить, что у человека слабое здоровье, часто простуды.

444 – говорит о крепком здоровье, спортсмен.

4444 – хорошее здоровье сочетается с высокой энергией, которая жаждет реализации в спорте или труде.

Недостатки: способны на обман, коварство. Хитрость.

Ячейка 5- Юпитер (Интуиция)

Если в квадрате одна 5 – человек со слабой интуицией, учится на собственном опыте и ошибках.

55 – человек интуитивно чувствует, что делать можно, а чего лучше избежать.

555 – мудрый человек, к его советам прислушиваются.

Недостатки: властолюбие, чванство и тщеславие

Ячейка 6- Венера (Физический труд)

Символизирует красоту души и гармонию, чувства и влечения, мягкость и уступчивость.

Венера способствует домовитости и создании в нем уютного пространства. Шестерка – это число миротворца и коммуникатора. Говорит о склонности к семейной жизни и комфорту в ней. Любители помогать другим людям.

Обладатели одной 6 – больше склонны к умственному труду, они избегают физический труд.

66 – любит работать физически, но не много. Может быть садоводом.

666 или 6666 – любит, как следует поработать и поесть.

Недостатки: лень, тунеядство, апатия.

Ячейка 7- Сатурн (Таланты личности)

Разум, стремление все систематизировать, одиночество, стойкость и выдержка. Сатурн способствует к самопознанию, глубокому анализу, понимать суть всего происходящего.

Семерка-это индивидуальность и способность охранять личную территорию. Цифра философа.

Если одна 7– имеет неяркий талант от рождения. Надо пробовать, чтобы найти себя.

77 – определенно есть талант, особенно в том, что делает.

777 или 7777 – высокоталантливый человек. Рано или поздно найдет выход.

Недостатки: мнительность и угрюмость.

Ячейка 8- Уран (Ответственность)

Изобретательство и реформаторство. Уран придает черты руководителя, который имеет чутье в обращении с деньгами, способность находить неординарные финансовые решения. Преобладание восьмерок говорит, что человеку уготована обеспеченная жизнь. Это финансисты.

Имея одну 8- человек необязателен. Многое прощает себе и другим.

88 – развито чувство долга, ответственный.

888–высокопринципиален, с сильным чувством долга и непогрешимости.

Недостатки: цинизм.

Ячейка 9- Нептун (Интеллект личности)

Высшая интуиция, медитация, способность видеть вещи с точки зрения вечности. Они могут мечтать о недостижимом, верят в светлые идеалы. Девятка – это склонность пожертвовать собой ради высокой цели, даже в ущерб реальности. Цифра духовности.

Если одна 9 – процесс обучения буде даваться с трудом, хотя учеба будет нравиться.

99 – это умные личности с хорошей памятью.

999 или 9999 – это ученые с прекрасной памятью и мышлением.

Недостатки: фанатизм и уход в иллюзии.

Количество цифр в ячейке имеет значение. Существует определенная норма для них. Для единиц, пятерок, восьмерок и девяток — это три. А остальных не должно быть больше одной. Если их больше нормы, то эти качества усилены, меньше – ослаблены. Но не расстраивайтесь, ослабленные качества обычно компенсируются другими чертами.

Кроме основных ячеек, существуют дополнительные. Необходимо посчитать количество цифр по строкам, по столбцам и по диагонали квадрата.

Сначала считаем количество цифр в строках.

Подсчет цифр верхней строки охарактеризует – Целеустремленность .

Показывает, насколько желания совпадают с возможностями.

Семейность -это вторая строка. Показывает, расположен ли человек к построению семьи и насколько он хорош, как семьянин.

Стабильность (привычки)- третья строка.

Говорит о надежности человека. Равновесие между привычками и стремлением к переменам.

Теперь считаем количество цифр в столбцах :

Количество крайнего левого столбца определят самооценку человека.

Заниженная самооценка покажет, что личность нерешительная, не верит в себя. Завышенная оценка влечет разочарование и кучу ошибок.

Цифры следующего столбца покажут уровень социального благополучия, статуса и благосостояния.

И количество цифр последнего столбца покажут талант человека от рождения. А реализация таланта уже будет зависеть от других качеств матрицы: целеустремленности, самооценки и трудолюбия.

Цифры диагонали скажут о влечении, темпераменте и духовности личности .

Спадающая диагональ слева направо скажет о духовности.

Не путайте это качество с религиозностью. В данном случае, это определяет убеждения и желание им следовать, равновесие между принципами и готовностью ими пожертвовать.

Слева направо восходящая диагональ покажет уровень темперамента. Этот показатель приобретает значение при определении совместимости партнеров. Идеально, чтобы партнеры не сильно отличались по темпераменту.

Древняя наука о числах поможет каждому человеку увидеть свои истинное предназначение в жизни. Софийская нумерология рассматривает имя и фамилию, как особый код. Расшифровав его, вы поймете, к чему у вас бесспорный талант. Это помогает в выборе профессии или хобби, а кому-то может помочь кардинально поменять жизнь. Число имени легко узнать из нумерологического алфавита. Если вы готовы к переменам, то удивите себя этой информацией.

Тайна имени раскроет не только ваши способности, вы можете узнать к чему лежит душа ребенка, вашей второй половинки.

Это древнее знание может облегчить жизнь, направить человека по нужному пути. У букв свое значение, и оно может сделать обладателя имени счастливейшим из людей. Если человек меняет имя или фамилию, то его судьба тоже изменится — не забывайте об этом.

Нумерология судьбы

Про то, что в числах скрыта величайшая тайна Вселенной, известно уже давно. Многие ученые посвятили свою жизнь нумерологии, а это наука наполовину точная, наполовину мистическая. У букв своя магия, которая откроется лишь тому, кто готов окунуться с головой в это тайное знание. Буквы окружают нас, в первую очередь — наше имя и фамилия. Родители выбирают приятные на слух имена, иногда — совершенно невероятные, придуманные.

Правильно они поступают или нет? Набор букв дает число имени, а оно определяет его дальнейшую жизнь, судьбу. Обязательно проверьте, какое имя вместе с фамилией даст вашему малышу удачливую судьбу. Если же вы со своим именем живете уже давно, то узнайте, как оно может вам помочь. У каждого из нас есть таланты, скрытые умения. Мы не всегда знаем о них, но если развивать — наши таланты могут принести нам не только удовлетворение, но и известность, славу, деньги.

Для любого алфавита можно рассчитать нумерологическую карту. Узнайте все про себя, своих близких и друзей. Все, что вам понадобится — полное имя, отчество и фамилия. Если ваш друг из страны, где не используется отчество, просто поставьте полное имя отца для расчетов. Это важно, ведь отчество — некий путеводный маяк, связывающий вашу жизнь и судьбу ваших родителей. В самом сокровенном кроется ответ на ваш вопрос «Кто же я?».

Что в имени тебе моем

Разные имена — разные судьбы. Повторение одного и того же имени в семье много раз — ошибка. Все позитивные качества его, конечно же, сохраняются, а негативные становятся родовой чертой. Тут, к сожалению:

алкоголизм, наркомания;
склонность к азартным играм;
склонность к изменам;
агрессивность, преступные наклонности.

Лучше вносить новые имена — они станут потоком свежего воздуха для вас и ваших потомков. Разнообразие, смешение культур идет на пользу вашей семье. Необычное имя может быть очень счастливым. Просчитайте его значение, с использованием алфавита русского языка. В латинской раскладке оно может давать другое значение.

Азбука имеет большое значение

Азбука имеет значение, ведь ребенок или взрослый будут его много раз писать, подписываться. Имя есть в паспортах, пропусках, на личных документах. Им оно тоже дает особую судьбу. Считается, что люди с длинными, звучными именами всегда счастливее. Это не обязательно так, ведь мы рассматриваем имя, как сочетание самого имени, отчества и фамилии. По сути, это три имени: ваше собственно, отца, целой семьи.

Таблицы значений

Уже все подсчитано, для каждого алфавита составлена таблица. Вам остается лишь подставить значение — это не сложно. Вычисления простые, любой с ними справится.

Значения русского алфавита (кириллица)

1	2	3	4	5	6	7	8	9
А	Б	В	Г	Д	Е	Ё	Ж	З
И	Й	К	Л	М	Н	О	П	Р
С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
Ъ	Ы	Ь	Э	Ю	Я

В таком порядке их и нужно использовать. Сочетаний букв и чисел даст вам конечное число. Если вы уже занимались подсчетами для классической нумерологии, то вам известно, как это делать. Если же нет, то пример подскажет.

Значения латинского алфавита

1	2	3	4	5	6	7	8	9
A	B	C	D	E	F	G	H	I
J	K	L	M	N	O	P	Q	R
S	T	U	V	W	X	Y	Z

Нумерологическая карта для латинского алфавита не отличается. Подсчеты ведутся точно так же.

Подсчет числа имени

НИКОЛАЙ 6+1+3+7+4+1+2=33=3+3=6

ВАСИЛЬЕВИЧ 3+1+1+1+4+3+6+3+1+7=66=6+6=12=3

ГОГОЛЬ 4+7+4+7+4+3=29=2+9=11=2

Мы получили три числа. Каждое из них имеет важное значение букв, которое можно рассматривать отдельно. Чтобы узнать конечное значение, сложим три числа:

Вот оно, число определяющее судьбу данного человека. Таким же образом нумерология позволяет подобрать имя для ребенка. У вас уже есть фамилия и, скорее всего, отчество. Выбирайте идеальное сочетание. Правда, такой способ может лишить вашего малыша важного — подарка от Фортуны. Родители, основном, руководствуются именно своими ощущениями от имени, а не подсчетом букв. Это дает ребенку шанс получить неожиданный талант.

Расшифровка числа имени

Азбука важна, но по сути, она нужна лишь для получения этого значения. Этот инструмент нумерологии используют с давних времен.

1

Человек не делает и шагу назад. Вся его жизнь — постоянное движение к задуманной цели. Вы встречали таких людей? У них на уме лишь любимое дело. Это может быть хобби, которое стало работой. С ними тяжело, никто не спорит. Но, обратите внимание — их задумка всегда превосходит ожидание. Человек с числом 1 всегда доводит дело до конца. Скорее всего, он избрал профессию юриста, экономиста, инвестиционного специалиста или занимается высокими технологиями. Реже эти люди — врачи, политики. Число 1 — трудное для своего обладателя, оно не позволяет отклоняться от задуманного пути на отношения, лишние чувства, переживания.

Единицы — люди действия

2

Число букв имени дало 2. Человек стремится к гармонии в жизни. Но, не может ее достичь. Он всегда не доволен, всегда хочется получить что-то лучше. Люди часто страдают от проблем со здоровьем, особенно психическим. Кажется, что он живет лишь одно ему известной жизнью. Всегда много планов, склонен к творческой деятельности. картины написаны лишь наполовину, все делается не до конца. Это часть его натуры — быстро разочаровываться в результатах своих трудов, еще не дождавшись результатов. Бывает, один раз им везет — они получают признание, овации, славу. Вся жизнь — напоминание о том моменте. Это тяжело, согласитесь. Поэты, художники, исследователи — вот их предназначение.

3

Для Троек главное — стабильность и баланс

Стабильные личности с числом имени 3. Нумерологическая азбука показывает 3, когда человек умеет находить гармонию в своем существовании. Тройка — первое из числе гармонии, оно говорит о том, что в духовном, материальном и личном плане человек достиг баланса. Он умеет быть одновременно разным, меняться, подстраиваться под обстоятельства. Найдет себе место практически в любой сфере деятельности, но чаще всего — врачи, конструкторы, учителя. Причем, они очень успешно занимаются своим делом. Людям с числом имени 3 можно только позавидовать, ведь они находят такой путь по жизни, который ведет прямой дорогой.

4

Четверка — второе из устойчивых числе. Оно характеризует 4 стихии. Гармония того числа колоссальная, так что человек умеет не только налаживать свою жизнь, но и вносить баланс в жизнь других людей. Чаще всего это социальные профессии, психология, массаж, люди, работающие с детьми. Если это ваше число, то вы наверное замечали — вас очень любят животные, люди тянутся к вам, дети всегда улыбаются. Это ваше внутреннее свойство отдавать видно издалека. Позитивный человек с огромными возможностями.

5

Пятёркам нужно себя контролировать

Пятерка — число очень опасное. Оно говорит о том, что человек часто отклоняется от задуманного плана. Тянет все бросить, начать что-то новое, придумать другой проект. Ему необходим постоянный контроль. В детстве это родители, а потом? Человек взрослый, а проблемы детские все еще остались. Ему хочется занимать руководящую должность, но сделать это тяжело, а если получается — провал неизбежен. Азбука вашего имени говорит о том, что просто необходимо взяться за себя обеими руками. Составляйте планы, графики, ведите дневник. Это поможет вам сконцентрироваться.

6

Третье гармоничное число, состоящее из двух троек или 2 и 4. Очень повезло тем, кто обладает им. Часто имена, дающие 6, специально дают детям. Человек находится в эпицентре событий, но не теряет головы; сосредоточен когда нужно, а после этого — может расслабиться, повеселиться; точно знает, как распределять свое время и любовь между родными, друзьями, работой, личной жизнью. Позитивное число 6 способно на многое. Это хорошие водители, прежде всего. Из профессий 6 выбирает юридические специальности, кулинарию, отлично владеет цифрами.

7

Семерка — число авантюриста. Очень часто эти люди не могут держать в руках деньги. Они буквально карман жгут. Есть большая опасность получить зависимость от азартных игр. Кажется, что колесо Фортуну поворачивается к вам, вот она — долгожданная удача. Период удачливый быстро проходит, а догнать Фортуну просто невозможно. Вместе с азартными играми приходит страсть к растратам, бесполезным покупкам. Обратите внимание, на что вы расходуете деньги, очень может быть, они так быстро утекают именно из-за неумения тратить. Этому человеку точно нельзя работать там, где есть наличные деньги.

Азартные Семёрки всегда в движении

8

Восьмерка говорит о том, что азбука вашего имени гармонична, хотя есть свои проблемы. Человек зациклен на материальном мире. Слишком много для вас значат вещи, предметы, деньги, доход. Вы полностью поглощены своей материальной жизнью, а о духовной сфере давно не задумывались. Речь идет не только о религиозном аспекте, но и просто о хорошем отдыхе, ценностях. Путешествие за город — удовольствие от природы, чистого воздуха. Хороша книга — впечатление, фантазия, мечта. Обед со старыми друзьями — смех, эмоции, веселье. Все это делает жизнь богаче духовно. Почему бы и нет? Вы привыкли работать, думать о своей семье, решать проблемы. Кто подумает о вас? Такой человек состоялся, как администратор, руководитель бизнеса, политолог, профессор университета.

9

Девятки — пророки среди людей

Софийская нумерология согласна здесь с классической. Люди с числом 9 — посланники небес. Они пришли с определенной целью в мир, несут свое бремя столько, сколько это необходимо. Их путь всегда чист, ведь Ангелы ведут человека с девяткой. Он точно знает, куда ступить, где свернуть, что делать дальше. Как? Не спрашивайте, просто верьте в него. Ему не легко от своей миссии, но он знак — если не он, то никто не сможет сделать это. Самое прекрасное, что после ее завершения, он ощущает небывалую свободу. То, что должно было случилось, он выполнил Божественное предназначение. Что будет дальше? Возможно, новый план ждет его, а пока — небольшой отдых.

Смена имени и фамилии

Сейчас модно менять имя. Человек может сам выбирать себе экзотическое имя, или же наоборот — сменить на более простое. Это хорошо, ведь мы можем вместе с ним поменять судьбу. Всегда подходите осмысленно к процессу смены, если решились. Смена букв поменяет ваше число имени, а вместе с ним могут прийти новые таланты. К сожалению, что-то старое точно уйдет.

Другая ситуация со сменой фамилии. Женщины делают это часто, просто чтобы поддержать традицию, сделать приятное мужу. Если вы видите, что новая фамилия принесет вам неприятности — лучше не менять. Нумерологическая азбука позволяет просчитать все возможные варианты. Почему нет, может ваш муж захочет в этом случае поменять фамилию?

Судьба находится в ваших руках. На число имени вы можете повлиять, к счастью. Если вам кажется, что:

судьба обходится с вами слишком сурово;
у вас ничего не получается;
не складываются отношения, любовь, дружба.

Задумайтесь, может дело в имени? Конечно, для того, чтобы решиться менять имя необходима очень веская причина, наличие всех этих пунктов сразу, например. Смена имен захватывает, но не всегда идет на пользу. Нельзя путаться судьбы. Смена возможна всего один раз в жизни, делать это чаще нельзя.

Обычные шифры из детективных романов часто устроены так: каждая буква сообщения заменяется каким-нибудь определённым значком или другой буквой. Подобные шифры очень ненадёжны, и вот почему. Буквы в текстах на русском языке (да и на любом языке вообще) встречаются неравномерно. Например, буква «О» в русских текстах встречается чаще всех других букв, а буква «Ъ» — реже всего. У каждой буквы есть своя примерная частота появления в тексте (смотри таблицу на поле справа).

Сочетания букв тоже встречаются неравномерно (например, «ьь» вообще не встречается). Конечно, все эти частоты зависят от конкретного текста — скажем, в биологической статье о жужелицах буква «ж» явно будет встречаться чаще, чем обычно. Но приведённая таблица вполне годится как ориентир.

Так вот, описанный способ шифровки не изменяет частот — просто теперь с аналогичной частотой будет появляться не сама буква, а заменяющий её значок. Высчитав частоту появления каждого значка в шифровке и сравнив полученные данные с таблицей частот, мы можем сделать предположения, какой букве какой значок соответствует. Далее пробуем заменять значки один за одним на буквы, проверяя свои догадки, корректируя их и делая новые, и постепенно расшифровываем текст. Если он не слишком короткий, мы с большой вероятностью его полностью расшифруем (хотя это может оказаться не совсем простым делом). Кстати, намного чаще любой буквы встречается пробел, разделяющий слова. Поэтому если пробел используется в шифровке и тоже заменён на какой-то значок, мы разгадаем его в первую очередь.

Совершенный шифр

Опишем теперь шифр, который принципиально не поддается расшифровке без знания ключа. Сопоставим каждой букве русского алфавита свою последовательность из 0 и 1 длины 5 (пятизначный двоичный код), например: А — 00000, Б — 00001, В — 00010 и так далее (или в каком-то другом порядке). Если буквы Е и Ё кодировать одинаково, то последовательностей как раз хватит (их 32, а в алфавите 33 буквы).

Заменим в тексте каждую букву на её двоичный код, получим последовательность из 0 и 1 (двоичный текст). Это пока ещё не шифровка — мы бы легко разгадали, какая буква на какую последовательность заменена (тем же методом, что и в случае замены букв на значки).

Чтобы зашифровать полученный двоичный текст, нам потребуется ещё ключ — случайная последовательность из 0 и 1 такой же длины. Этот ключ должен быть и у отправителя шифрованного сообщения, и у адресата.

Для зашифровки просто складываем две последовательности нулей и единиц — двоичный текст сообщения и ключ: первую цифру с первой, вторую со второй, и так далее. Но складываем по особым правилам:

0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 0

(в математике это называется сложением по модулю 2).

Полученная последовательность и будет зашифрованным сообщением. Чтобы расшифровать её, надо просто… снова прибавить к ней ключ! Тогда мы как бы прибавим к исходной последовательности ключ два раза. А по нашим правилам, прибавляя две одинаковые цифры мы ничего не меняем, то есть мы вернёмся к исходному двоичному тексту. Схематически процесс шифрования и дешифрования можно описать так:

текст + ключ = шифровка;

шифровка + ключ = текст + ключ + ключ = текст.

Ясно, что расшифровать сообщение, не зная ключа, невозможно. Нам как бы дана сумма двух чисел, и нельзя восстановить одно из слагаемых, ничего не зная про другое. Имея на руках лишь шифровку, мы знаем только, что исходный текст может быть абсолютно любым текстом соответствующей длины. Ведь по любому такому тексту можно изготовить ключ, который приведёт ровно к той же самой шифровке!

Недостаток описанного способа в том, что каждый текст требует нового ключа такой же длины — если повторять ключи, появляется возможность расшифровки. Например, мы могли бы попробовать вместо длинного ключа использовать ключ всего из пяти символов, скажем 11010. Разбиваем двоичный текст на пятёрки цифр и прибавляем к каждой пятёрке 11010. Фактически, мы просто заменяем каждую пятёрку цифр на какую-то другую фиксированную пятёрку. В этом случае расшифровать исходный текст так же легко, как если бы мы просто заменили его двоичным кодом, не прибавляя никакого ключа. Использовать длинные ключи, но всё же существенно более короткие, чем текст, тоже опасно — есть метод определения длины ключа, а после того как длина ключа установлена, можно применить частотный анализ.

Поэтому надо заготовить ключ огромной длины заранее и лишь указывать, например, в начале шифровки, какое место ключа используется. При этом очень важно, чтобы ключ был случайной последовательностью из 0 и 1. Например, последовательности 11111111111111111 и 010101010101010 не случайные. Кстати, придумать случайную последовательность не так-то просто. Трудно даже (но возможно) дать чёткое определение, какие последовательности могут считаться случайными.

Немного истории и литературы

Подобный шифр использовал Макс Кристиансен-Клаузен, шифровальщик выдающегося советского разведчика Рихарда Зорге. Наиболее часто употребляемые буквы английского алфавита s, i, o, e, r, a, t, n заменялись цифрами от 0 до 7, а остальные буквы — числами от 80 до 99 (чтобы не возникало путаницы, когда числа записывались подряд). Ключом служили старые выпуски «Статистического ежегодника Германского рейха» с множеством числовых данных. Ключ записывали под текстом и прибавляли, причём если сумма двух цифр превышала 10, то записывалась только её последняя цифра. Например, вместо 7 + 5 писали 2, отбрасывая десяток (в математике это называется сложением по модулю 10). Восстанавливали исходное сообщение, «вычитая» ключ из шифровки. Когда выходило отрицательное число, как, скажем, при вычитании 5 из 2, было ясно, что надо вычитать из числа на 10 больше, то есть из 12 — вот и получали 7.

Японские тайные службы перехватили много радиограмм Зорге, но ни одной не сумели расшифровать. Более полный рассказ об этом читайте в замечательной книге Юлиуса Мадера «Репортаж о докторе Зорге».

А герой приключенческих романов Юлиана Семёнова «Семнадцать мгновений весны» и «Приказано выжить» разведчик Штирлиц, больше известный нам по знамениту кинофильму, использовал в качестве ключа художественную книгу Монтеня. При этом осмысленный текст сообщения«складывался» с осмысленным же (и значит, не случайным!) текстом ключа. Когда германским контрразведчикам стало известно предполагаемое содержание одной из шифровок, в частности — некоторые слова, которые там могли встречаться, — они попробовали их подставить в разные места шифровки и посмотреть, какой получается ключ. Попав в нужное место, они открывали кусочек ключа, в котором угадывались части осмысленных слов. Восстанавливая эти слова, они раскрывали и новый кусочек шифровки, и так постепенно расшифровали её.

Шифры с открытым ключом

Начиная с 1977 года, стали появляться новые шифры, основанные на глубоких математических идеях, высказанных американскими математиками Диффи и Хеллманом за два года до этого. Представьте себе, что два бизнесмена хотят переписываться друг с другом, надёжно шифруя сообщения, но забыли договориться о ключе. Они находятся в разных странах, всё их общение может прослушиваться конкурентами. Как тут быть? Оказывается, выходы есть. Опишем один из них, но без подробностей, только сам принцип.

Придуман способ шифровки, для которого надо знать лишь произведение pq двух каких-то простых чисел p и q , а сами числа p и q знать не нужно. А вот для расшифровки сообщения обязательно иметь в распоряжении и число p , и число q . «Ну и что тут такого?», — спросите вы. А вот что. Дело в том, что эти простые числа можно взять очень большими. И тут мы сталкиваемся с таким явлением: современные компьютерные мощности огромны, но всё же ограничены. Скажем, компьютер может за разумное время разложить на простые множители 200-значное число, но раскладывание 300-значных чисел ему уже не под силу (любому из известных алгоритмов потребуются многие годы). Всегда есть какая-то подобная граница. А выяснить про число, простое оно или нет, компьютеры могут очень быстро для гораздо более длинных чисел. Так вот, первый из компаньонов может с помощью компьютера найти какие-нибудь два, скажем, 400-значных простых числа p и q , перемножить их и открыто переслать результат второму (а сами числа p и q хранить в тайне). Получив произведение pq , тот зашифрует своё сообщение и отправит обратно первому. И первый его легко расшифрует — он-то знает оба числа p и q . А вот всяким там подслушивателям для расшифровки придётся сначала разложить на множители произведение pq , в котором 800 знаков — а с этим не справится ни один современный компьютер! Этот метод шифровки называется RSA, по первым буквам фамилий его создателей — Ривеста, Шамира и Адлемана.

Конечно, с развитием компьютерных технологий появляется возможность расшифровывать старые сообщения. Первая шифровка авторов RSA, опубликованная ими в 1977 году как вызов всем дешифровальщикам мира, продержалась 17 лет. Также есть опасность, что будет найден новый, быстрый алгоритм разложения чисел на простые множители. Но есть математическая гипотеза, что все такие алгоритмы работают принципиально не быстрее, чем уже известные.

А у вас получится?

Перед вами текст, который получен из хорошо известного заменой каждой буквы на какую-то другую. Расшифруйте его.

Атокг ацынг цлекытуы цлауенг ьи Чолсв, и уими Чолси уманлоти ки эекпв нипеме вматыфюеме, цаткзме утоь чтиьиме, жна ни ацынг ьималчити, андоти атокы д уналакв е, мокыы омв ки чатадо тхс, боцквти:
– Пиё д уимам сото в Укоркаё палатодз, ка ак дцатко садаток е свмион, жна твжбо омв кечсо е щзнг ко марон. Цлежекаё ро дуомв аупатпе ьолпити, жна уесын в коча д уолсйо е д чтиьв. Еш киса вситенг, екижо ак кепачси ко щвсон жотадопам, е Укоркиы палатоди уашликен кис кем удаф дтиунг.
– Ка ко цамаробг те нз Чолсо пип-кещвсг вкежнаренг янв дтиунг?
– Уетгкоо, жом аки оунг, ы ко мачв ох усотинг. Ко десебг лиьдо, пип дотепи ох уети? Ко десебг, жна оё утврин е тфсе е реданкзо? Досг аки щауиы ащабти цатудони! Ко в киу ьикеминг оё уетв! Уети — д ох метам, кодеккам сонупам уолсожпо. Оуте аки уими ко умарон цлакепквнг д жолначе Укоркаё палатодз е еьдтожг еь уолсйи Пиы аупатпе, на мз е цасидка оё ко цамаром! Д сдвш метыш ануфси кижекионуы уис Укоркаё палатодз. Анкоуе нвси содажпв, уцвуне в щатгбача пвуни, цаплзнача плиукзме ычасиме, е, ко мобпиы, даьдлиюиёуы ащлинка!
У янеме утадиме эекпи цасуисети Чолсв ки уцекв атокы, е нан щлауетуы щоринг уа дуош кач.

С той самой поры, как человечество доросло до письменной речи, для защиты сообщений используются коды и шифры. Греки и египтяне использовали шифры для защиты личной переписки. Собственно говоря, именно из этой славной традиции и произрастает современная традиция взлома кодов и шифров. Криптоанализ изучает коды и методы их взлома, и это занятие в современных реалиях может принести немало пользы. Если вы хотите этому научиться, то можно начать с изучения самых распространенных шифров и всего, что с ними связано. В общем, читайте эту статью!

Шаги

Расшифровка шифров замещения

Начните с поиска слов из одной буквы. Большинство шифров на основе относительно простой замены легче всего взломать банальным перебором с подстановкой. Да, придется повозиться, но дальше будет только сложнее.

Слова из одной буквы в русском языке — это местоимения и предлоги (я, в, у, о, а). Чтобы найти их, придется внимательно изучить текст. Угадывайте, проверяйте, закрепляйте или пробуйте новые варианты — иного метода разгадки шифра нет.
Вы должны научиться читать шифр. Взламывать его — это не столь важно. Учитесь выхватывать шаблоны и правила, лежащие в основе шифра, и тогда его взлом не будет представлять для вас принципиальной сложности.

Ищите наиболее часто употребляемые символы и буквы. К примеру, в английском языке такими являются “e”, “t” и “a”. Работая с шифром, используйте свое знание языка и структуры предложений, на основе чего делайте гипотезы и предположения. Да, на все 100% вы редко будете уверены, но разгадывание шифров — это игра, где от вас требуется делать догадки и исправлять собственные ошибки!

Двойные символы и короткие слова ищите в первую очередь, старайтесь начать расшифровку именно с них. Легче, как никак, работать с двумя буквами, чем с 7-10.

Обращайте внимание на апострофы и символы вокруг. Если в тексте есть апострофы, то вам повезло! Так, в случае английского языка, использование апострофа означает, что после зашифрованы такие знаки, как s, t, d, m, ll или re. Соответственно, если после апострофа идут два одинаковых символа, то это наверняка L!

Попробуйте определить, какой у вас тип шифра. Если вы, разгадывая шифр, в определенный момент поймете, к какому из вышеописанных типов он относится, то вы его практически разгадали. Конечно, такое будет случаться не так уж и часто, но чем больше шифров вы разгадаете, тем проще вам будет потом.

Цифровая замена и клавиатурные шифры в наши дни распространены более всего. Работая над шифром, первым делом проверяйте, не такого ли он типа.

Распознавание обычных шифров

Шифры замещения. Строго говоря, шифры замещения кодируют сообщение, замещая одни буквы другими, согласно заранее определенному алгоритму. Алгоритм — и есть ключ к разгадке шифра, если разгадать его, то и раскодировать сообщение проблемы не составит.
- Даже если в коде есть цифры, кириллица или латиница, иероглифы или необычные символы — пока используются одни и те же типы символов, то вы, вероятно, работаете именно с шифром замещения. Соответственно, вам надо изучить используемый алфавит и вывести из него правила замещения.
Квадратный шифр. Простейшее шифрование, используемое еще древними греками, работающее на основе использования таблицы цифр, каждая из которых соответствует какой-то букве и из которых впоследствии и составляются слова. Это действительно простой код, своего рода — основа основ. Если вам надо разгадать шифр в виде длинной строки цифр — вероятно, что пригодятся именно методы работы с квадратным шифром.
Шифр Цезаря. Цезарь умел не только делать три дела одновременно, он еще и понимал в шифровании. Цезарь создал хороший, простой, понятный и, в то же время, устойчивый ко взлому шифр, который в его честь и назвали. Шифр Цезаря — это первый шаг на пути к изучению сложных кодов и шифров. Суть шифра Цезаря в том, что все символы алфавита сдвигаются в одну сторону на определенное количество символов. Например, сдвиг на 3 символа влево будет менять А на Д, Б на Е и т.д.
Следите за клавиатурными шаблонами. На основе традиционной раскладки клавиатуры типа QWERTY в наше время создаются различные шифры, работающие по принципу смещения и замещения. Буквы смещаются влево, вправо, вверх и вниз на определенное количество символов, что и позволяет создать шифр. В случае таких шифров надо знать, в какую сторону были смещены символы.
- Так, меняя колонки на одну позицию вверх, “wikihow” превращается в “28i8y92”.
- Полиалфавитные шифры. Простые замещающие шифры опираются на создание шифрующим своего рода алфавита для шифрования. Но уже в Средние века это стало слишком ненадежно, слишком просто для взлома. Тогда криптография сделала шаг вперед и стала сложнее, начав использовать для шифрования символы сразу нескольких алфавитов. Что и говорить, надежность шифрования сразу повысилась.

Что значит быть дешифровальщиком

Будьте терпеливы. Взломать шифр — это терпение, терпение и еще раз терпение. Ну и упорство, конечно же. Это медленная, кропотливая работа, сопряженная с большим количеством разочарования из-за частых ошибок и необходимости постоянно подбирать символы, слова, методы и т.д. Хороший дешифровальщик просто обязан быть терпеливым.

«Такое не взломает даже квантовый компьютер» – Огонек № 19 (5564) от 20.05.2019

Сенсация: в Бристольском университете якобы смогли прочесть самую таинственную рукопись мира — манускрипт Войнича. «Огонек» разобрался, как находят скрытое и расшифровывают тайное.

Британский лингвист Герард Чешир удивил мир: он утверждает, что смог прочесть легендарный манускрипт Войнича. Речь про иллюстрированный кодекс XV века, найденный книготорговцем Уилфридом Войничем и состоящий из 240 страниц загадочного текста с астрономическими знаками, растениями, сосудами и людьми. Правда, утверждается, что это вовсе не шифр, а текст на давно утраченном — протороманском — языке. Сам манускрипт представляет собой справочник по разным вопросам (в частности, по медицине и истории), составленный доминиканскими монахами для Марии Кастильской, королевы Арагона. Вся рукопись целиком пока не прочитана, но Герард обещает завершить начатое: еще в апреле он представил первые результаты на суд коллег и общественности в журнале Romance Studies. Остается дождаться реакции — такие сенсационные заявления звучат не в первый раз.

Впрочем, вне зависимости от того, чем закончится история с манускриптом Войнича, можно смело констатировать: криптография сегодня на пике моды. В информационном поле то и дело всплывают новости о расшифровке таинственных посланий, а с экранов не сходят сериалы о специалистах-шифровальщиках. Сразу два таких сериала (отечественный «Шифр» и британский «Код убийства») напомнили о военной (и послевоенной) истории криптографии. С одной из самых известных легенд того времени — взлома немецкой шифровальной машины «Энигмы» — мы и начали разговор с ученым (МФТИ), автором труда по защите информации Сергеем Владимировым.

— Вы наверняка знаете про то, как британцы взломали «Энигму», кинематографисты не устают снимать фильмы на эту тему. Достижение и правда столь выдающееся?

— Как вам сказать… Некоторые считают, что благодаря взлому «Энигмы» длительность Второй мировой войны сократилась на пару лет. Напомню, что немцы использовали эту роторную машину для шифрования и расшифровки секретных сообщений, причем такие аппараты существовали и у американцев, и у нас. Однако история, конечно, приобрела всемирную известность благодаря своим масштабам: количество шифровок «Энигмы» исчислялось тысячами.

Приоритет в ее расшифровке принадлежит полякам — трем специалистам из «Бюро Шифров» — подразделения польской военной разведки. Сама «Энигма», по сути, представляла собой плохой полиалфавитный шифр, плохой в том смысле, что ключи соседних букв были связаны по определенным правилам — в механическом устройстве невозможно по-другому. Но если поляки занимались в основном ручной расшифровкой, то британцы из Блетчли-парка создали электромеханические машины, помогавшие взломать немецкий код. В том числе для взлома шифров они собрали первый в мире компьютер, вот почему эту историю трудно переоценить. К сожалению, науки у нас развиваются в тени войн. Первая мировая война — это механическая криптография и криптоаналитика (взлом шифров.— «О»), Вторая мировая — это Блетчли-парк и «Энигма»…

А вот вам еще один парадокс: «Энигма» стала известна именно потому, что ее взломали. Это как с разведчиками — мир узнает о них только тогда, когда их раскрывают.

— С «Энигмой» понятно. А что бы вы назвали главным событием в истории криптографии?

— Пожалуй, создание криптографии на открытых ключах, которая используется до сих пор. Это произошло уже в 1970-х. Понимаете, классическая симметричная криптография имеет дело с одним ключом, или кусочком информации, нужным для шифрования и последующей расшифровки. Допустим, таким ключом может быть цифра (в случае сдвига шифра по алфавиту, как в шифре Цезаря) или целая книга. Этот принцип не менялся тысячелетиями и остается актуален до сих пор. Однако в криптографии на открытых ключах нашли новый подход: теперь для шифрования нужен один ключ, а для расшифровки другой. Для нас, криптографов, это, конечно, была настоящая революция.

Текст на затылке

— Давайте ненадолго вернемся в прошлое. Когда люди впервые начали шифроваться и главное — что пытались скрыть?

— Насколько мне известно, самый ранний пример шифров — это древнеиндийский аналог русского «Домостроя», с разделом о женском календаре. Календарь был зашифрован, чтобы его не могли прочесть мужчины. Так что история криптографии насчитывает уже несколько тысяч лет.

— Насколько сложны были шифры древности?

— Судите сами: в знаменитом шифре Цезаря, изобретенном им самим, буквы «сдвигались» на определенное число по алфавиту. Выбирался ключ (например, число 3), а дальше вместо А ставилась третья буква — В, вместо Б — Г и так далее. Когда варвары видели зашифрованный таким образом текст, они думали, что это просто неизвестный им язык. Но долго этот шифр не продержался: его быстро научились «взламывать».

Анализируй это

«Огонек» попросил Сергея Владимирова составить специально для нашего журнала несколько простых криптографических задач. Вот они — теперь каждый может примерить на себя роль дешифровщика

Смотреть

Интересно, что первые криптоаналитики появились еще раньше, одним из них был Аристотель. Он догадался, как взломать шифр, созданный с помощью скиталы. Напомню: скитала представляла собой палку, на которую тонкой лентой наматывался папирус. Далее вдоль палки на намотанную ленту писался текст, и когда папирус снимался — текст сразу становился не читаем. Просто набор букв. Это еще называется геометрическим шифром, когда мы меняем не сами буквы, а их положение в тексте. Так вот Аристотель взял конус, намотал на него ленту с шифром и просто стал сдвигать ее вдоль конуса, пока не получил читабельный текст.

— Остроумно. Похоже на соревнование брони и снаряда: чем лучше броня, тем бронебойнее снаряды…

— Совершенно верно! Например, довольно долго использовались моноалфавитные шифры (когда текст заменяется на другой согласно одному правилу, побуквенно), такой шифр применяла Мария Стюарт в своей секретной переписке. Правда, она использовала модернизированный вариант: шифровала одни и те же буквы разными символами… Однако ее переписку все равно смогли перехватить и расшифровать, а Мария поплатилась за это головой. Так что, когда моноалфавитные шифры стали совсем ненадежными, мир перешел на полиалфавитные (допустим, для четных букв используется одно правило шифрования, а для нечетных — другое). Но к началу XX века криптоаналитики научились взламывать большинство шифров. Главное, что нужно было угадать,— на сколько групп разбит нужный шифр, а затем «ломать» каждую из них. Наконец, настоящий прорыв случился в середине ХХ века — с появлением шифрования на открытых ключах. Если до этого криптография была своего рода искусством, то затем началась эра науки — математики.

— Надо было брать пример с Ленина, он, как известно, вообще писал молоком…

— А это уже стеганография, или искусство скрытого письма. Когда речь не столько про шифр, сколько про то, чтобы скрыть некий текст. Стеганографию тоже применяли в далекой древности, правда, необычно: на бритой голове раба писали сообщение, дожидались, пока волосы у него отрастут, и отправляли к адресату. Желательно, чтобы раб при этом еще был немым и не мог выдать своего секрета.

Самый надежный шифр

— Вернемся к шифрованию. Я навскидку назову так и не взломанные шифры: манускрипт Войнича, послания американского маньяка Зодиака… Почему их так и не смогли «расколоть»?

— А были ли связные тексты за этими шифрами? Например, в случае с манускриптом Войнича некоторые ученые уверены, что это просто случайный набор символов. Мистификация.

Я не утверждаю, что это именно так. Но тут встают и чисто математические сложности. Например, для полноценной расшифровки нужен большой объем текста, если его не хватает, ничего не получится. Или еще одна интересная проблема — соотношение длины ключа и длины текста. Если в манускрипте Войнича один ключ на всю книгу, тогда расшифровка возможна. Если же на каждой странице использовался свой ключ — дело безнадежное. Наконец, помните, что это просто игра: никаких экономических или военных плюсов расшифровка этого манускрипта не принесет, а значит, вполне вероятно, что за него не брались всерьез.

— Выходит, шифр, который нельзя расшифровать, все же существует?

— Конечно! Например, шифроблокноты, их до сих пор используются дипломатами. Это такие блокноты, которые прошиты с четырех сторон особыми нитками. На каждой странице — цифры, они являются ключом. Когда нужно зашифровать текст, берутся цифры с первой страницы, текст с их помощью зашифровывается, а затем страница срывается и сжигается. После шифровка пересылается адресату. У адресата есть точно такой же шифроблокнот с таким же ключом на нужной странице. С его помощью он и расшифровывает сообщение. Все! Идея шифроблокнота в том, что длина ключа, с помощью которого зашифровано сообщение, равна длине текста. При этом если ключ выбран случайно, то текст невозможно взломать при условии, что каждая буква шифруется по отдельности и никакой ключ не используется два раза. Такое не взломает даже квантовый компьютер. Точнее, способ взлома все-таки есть — его еще называют «метод утюга и паяльника». Но это уже другая история.

Один из основателей современной криптографии, американский математик Клод Шеннон, некогда придумал способ измерить то, насколько шифр надежен, с помощью теории вероятности. Так вот Шеннон доказал, что шифроблокнот — абсолютно надежный шифр. Никакими математическими методами его не взломать.

Ключи эпохи интернета

— А насколько современная криптография приблизилась к таким вот идеальным шифрам?

— Можно сказать, подошла вплотную. Смотрите: сейчас криптография строится на двух китах — той самой симметричной криптографии и криптографии на открытых ключах. Ну, например, симметричная криптография — в основе современных госстандартов шифрования. Сам ключ сегодня представляет собой большую формулу (по сути, с десяток страниц текста, описывающего процесс шифрования). Но, конечно, криптографы думают над тем, как сделать этот ключ меньше и при этом столь же стойким к взлому. Это развитие идей американца Клода Шеннона: попытка придумать алгоритм, когда маленький ключ может так замешать и запутать текст, что его нельзя «прочитать».

— И где такое шифрование применяется?

— Да, в общем, везде, просто в разных видах. Ну, например, в сотовой связи, когда ваш телефон вырабатывает ключ для связи с сотовой вышкой. Или при подключении монитора к компьютеру — они общаются друг с другом по зашифрованному каналу (это было сделано для того, чтобы пираты не могли скопировать видеосигнал). Или автомобильный брелок…

— А шифрование на открытых ключах?

— Спектр его применения тоже широк, но среди основных сфер — IT. В шифровании на открытых ключах, напомню, совсем другая основа — математика. Ну, например, взяли два больших простых числа, перемножили их и получили еще большее число. Теперь математическая проблема: как из этого восстановить простые числа? Например, число 15 легко раскладывается на 5 и 3. Но, когда у нас числа имеют размер в тысячи десятичных знаков, проблема с практической точки зрения уже становится нерешаемой.

Давайте я коротко напомню, как работает такое шифрование: мы шифруем информацию открытым ключом, а расшифровываем закрытым. При этом открытый ключ не составляет никакой тайны: то есть зашифровать сообщение с его помощью может любой. Но вот расшифровать может только получатель, у которого есть второй, закрытый, ключ. Плюс этой технологии в том, что для нее можно использовать открытые каналы связи, например интернет или мессенджеры.

— Правильно ли я понимаю, что блокчейн основан на той же технологии?

— Да, там используется криптография открытого ключа и немного симметричного шифрования. Например, чтобы перевести деньги с кошелька на кошелек, вы должны создать транзакцию и подписать ее своим открытым ключом.

Но если мы вспомним алгоритм майнинга биткойнов, то он несколько другой. Майнинг состоит в том, что вы перебираете числа одно за другим, применяете к ним криптографическую функцию и смотрите, что получилось на выходе. Как только на выходе получается число с определенным количеством нулей — ура! Вы откопали «монетку». Для чего здесь нужна криптографическая функция? Очень просто: для того, чтобы процесс нельзя было «провернуть» назад, узнать исходное число и майнить столько, сколько хочешь. Так вот здесь уже используется симметричное шифрование.

— Все равно как-то не верится, что все это нельзя взломать…

— Почему же нельзя. Бывают так называемые бэкдоры — лазейки, которые оставляют разработчики тех или иных криптографических средств. Например, печально известна микросхема Clipper для шифрования, которую пытались навязать всем американским разработчикам средств связи и защиты информации еще в 1990-х. Быстро выяснилось, что там была такая лазейка. Американцы встроили бэкдор и в свой стандарт генерации случайных чисел для криптографии. Его потом обнаружили и исключили, но осадочек остался.

— А что именно хотели получить наши спецслужбы в рамках знаменитого «пакета Яровой»? Речь там тоже шла о криптографии…

— Речь шла не о дешифровке, а о самом процессе передачи зашифрованной информации. Возьмем интернет.

Во многих социальных сетях общение людей зашифровано только на уровне «клиент — сервер», то есть его невозможно прочитать, пока оно «идет», зато непосредственно на сервере — сколько угодно. Там оно хранится в расшифрованном виде.

А вот в некоторых мессенджерах шифруется канал общения от пользователя до пользователя, то есть, по сути, до конкретного устройства. И когда компетентные органы обращаются к владельцу сервиса, чтобы получить текст сообщения, тот лишь разводит руками: он тоже видит его лишь в зашифрованном виде. Проблема в том, что расшифровать это невозможно, сколько законов ни принимай.

Наше светлое криптобудущее

— Давайте перейдем к квантовым компьютерам. Говорят, они скоро смогут «расколоть» любой шифр. Не верите?

— Не в ближайшие лет пять точно. Чтобы квантовый компьютер смог расшифровать более или менее длинный код, зашифрованный открытым ключом, ему понадобится объем, скажем, в 2 тысячи кубитов (это элементы для хранения информации в квантовом компьютере.— «О»). А сегодня успешно строят компьютеры примерно в 15 кубитов. Пока эта инженерная проблема не преодолена, квантовый компьютер неэффективен.

К тому же сейчас мир переходит на шифрование с помощью эллиптических кривых, они для квантового компьютера и вовсе крепкий орешек. Объясняю, как это работает: представьте, что мы можем складывать точки на параболе как числа или даже умножать их на целые числа. В таком случае можно узнать, какая точка была в начале, какую точку мы получили в конце. Но быстро понять, на какое число ее умножили, очень трудно. Эта чисто математическая проблема и лежит в основе эллиптической криптографии. Так вот квантовый компьютер сможет разве что сократить перебор вариантов на сколько-то порядков. Но если ключ сам по себе длинный, это бесполезно.

— Какие же тогда перспективы у криптографии? Как будем шифроваться в ближайшем будущем?

— В целом современная криптография переходит в прикладную область: создание не просто шифров, а правил их использования. Например, у вас есть сервер социальной сети, вы как пользователь пытаетесь к нему обратиться. Но где гарантия, что это не копия сервера, созданная злоумышленниками? Есть различные способы решения этой проблемы: допустим, организация доверенных серверов. Над этим и думаем.

Что же касается перспектив… К примеру, есть большой математический вызов: решение нелинейных уравнений в дискретном поле. Не буду сейчас вдаваться в подробности, но лишь отмечу, что, если их научатся быстро решать, симметричная криптография падет — такие шифры смогут легко взламывать.

Беседовал Кирилл Журенков

5 интересных систем шифрования. Разгадайте секретные слова | Конкурсы и тесты

В этот день свой профессиональный праздник отмечает Криптографическая служба России.

«Криптография» с древнегреческого означает «тайнопись».

Как раньше прятали слова?

Своеобразный метод передачи тайного письма существовал во времена правления династии египетских фараонов:

выбирали раба. Брили его голову наголо и наносили на неё текст сообщения водостойкой растительной краской. Когда волосы отрастали, его отправляли к адресату.

Шифр — это какая-либо система преобразования текста с секретом (ключом) для обеспечения секретности передаваемой информации.

АиФ.ru сделал подборку интересных фактов из истории шифрования.

Все тайнописи имеют системы

1. Акростих — осмысленный текст (слово, словосочетание или предложение), сложенный из начальных букв каждой строки стихотворения.

Вот, например, стихотворение-загадка с разгадкой в первых буквах:

Довольно именем известна я своим;
Равно клянётся плут и непорочный им,
Утехой в бедствиях всего бываю боле,
Жизнь сладостней при мне и в самой лучшей доле.
Блаженству чистых душ могу служить одна,
А меж злодеями — не быть я создана.
Юрий Нелединский-Мелецкий
Сергей Есенин, Анна Ахматова, Валентин Загорянский часто пользовались акростихами.

2. Литорея — род шифрованного письма, употреблявшегося в древнерусской рукописной литературе. Бывает простая и мудрая. Простую называют тарабарской грамотой, она заключается в следующем: поставив согласные буквы в два ряда в порядке:

употребляют в письме верхние буквы вместо нижних и наоборот, причём гласные остаются без перемены; так, например, токепот = котёнок и т. п.

Мудрая литорея предполагает более сложные правила подстановки.

3. «ROT1» — шифр для детишек?

Возможно, в детстве вы тоже его использовали. Ключ к шифру очень прост: каждая буква алфавита заменяется на последующую букву.

А заменяется на Б, Б заменяется на В и так далее. «ROT1» буквально означает «вращать на 1 букву вперёд по алфавиту». Фраза «Я люблю борщ» превратится в секретную фразу «А мявмя впсъ». Этот шифр предназначен для развлечения, его легко понять и расшифровать, даже если ключ используется в обратном направлении.

4. От перестановки слагаемых…

Во время Первой мировой войны конфиденциальные сообщения отправляли с помощью так называемых перестановочных шрифтов. В них буквы переставляются с использованием некоторых заданных правил или ключей.

Например, слова могут быть записаны в обратном направлении, так что фраза «мама мыла раму» превращается во фразу «амам алым умар». Другой перестановочный ключ заключается в перестановке каждой пары букв, так что предыдущее сообщение становится «ам ам ым ал ар ум».

Возможно, покажется, что сложные правила перестановки могут сделать эти шифры очень трудными. Однако многие зашифрованные сообщения могут быть расшифрованы с использованием анаграмм или современных компьютерных алгоритмов.

Диск с шифром Цезаря. Фото: mr.santak/commons.wikimedia.org

5. Сдвижной шифр Цезаря

Он состоит из 33 различных шифров, по одному на каждую букву алфавита (количество шифров меняется в зависимости от алфавита используемого языка). Человек должен был знать, какой шифр Юлия Цезаря использовать для того, чтобы расшифровать сообщение. Например, если используется шифр Ё, то А становится Ё, Б становится Ж, В становится З и так далее по алфавиту. Если используется шифр Ю, то А становится Ю, Б становится Я, В становится А и так далее. Данный алгоритм является основой для многих более сложных шифров, но сам по себе не обеспечивает надёжную защиту тайны сообщений, поскольку проверка 33-х различных ключей шифра займёт относительно небольшое время.

Никто не смог. Попробуйте вы

Зашифрованные публичные послания дразнят нас своей интригой. Некоторые из них до сих пор остаются неразгаданными. Вот они:

Манускрипт Войнича. «Ботанический» раздел содержит изображения растений. Фото:commons.wikimedia.org

Манускрипт Войнича

Это 240-страничная книга, написанная на абсолютно неизвестном языке с цветными рисунками и странными диаграммами, изображениями невероятных событий и растений, которые не похожи ни на один известный вид.

Криптос у штаба ЦРУ в Лэнгли, штат Вирджиния. Фото: Jim Sanborn/commons.wikimedia.org

Криптос. Скульптура, созданная художником Джимом Санборном, которая расположена перед штаб-квартирой Центрального разведывательного управления в Лэнгли, Вирджиния. Скульптура содержит в себе четыре шифровки, вскрыть код четвёртой не удаётся до сих пор. В 2010 году было раскрыто, что символы 64-69 NYPVTT в четвёртой части означают слово БЕРЛИН.

Криптограмма № 1 — местонахождение тайника. Фото: commons.wikimedia.org

Шифр Бэйла — это комплект из трёх шифровок, которые, предположительно, раскрывают местонахождение одного из величайших захороненных сокровищ в американской истории: многих тысяч фунтов золота, серебра и драгоценных камней.

Теперь, когда вы прочитали статью, то наверняка сможете разгадать три простых шифра.

Свои варианты оставляйте в комментариях к этой статье. Ответ появится в 13:00 13 мая 2014 года.

Ответ:

1) Блюдечко

2) Слоненку все надоело

3) Хорошая погода

Смотрите также:

Расшифровка цифр расчетного счета: структура и значение номера

Коротко о главном:

В статье разберемся, как расшифровываются расчетные счета. Узнаем, что означает структура из цифр, какие есть разделы в номере и как определить, чей это банковский счет — ИП, юридического или физического лица.

Структура номера банковского счета — это набор цифр в строгой определенности, значение которых нетрудно расшифровать. Даже частичная расшифровка номера дает понять, в какой валюте оформлен счет и для каких операций он может использоваться. Ниже рассмотрим особенности расшифровки расчетного счета.

Как выглядит структура расчетного счета

Номер счета включает 20 знаков, шесть разделов, в каждый заложена конкретная информация. Для удобства представим эти разделы в виде «111 22 333 4 5555 6666666», где цифры обозначают:

111	кто оформил счет
22	чем занимается владелец
333	валюта
4	ключ
5555	филиал банка, где был оформлен счет
6666666	индивидуальный номер в филиале

Как расшифровываются первые 5 цифр счета

Нумерация банковского расчетного счета дает понять, кому он принадлежит. Например, если счет начинается с «407», то он принадлежит юридическому лицу, ИП или некоммерческой организации. Если на «408» — то оформлен на физ. лицо.

Следующие две цифры («22») дополняют предыдущий блок, их можно расшифровать только в связке с ним. Эти разряды говорят о назначении используемых средств. Разберем расшифровку цифр в случае с юр. лицами (407…):

40701	финансовая сфера
40702	акционерные общества, общества с ограниченной ответственностью и т.д.
40703	платежи НКО
40704	финансирование выборов, общественных собраний и пр.

Рекомендуем прочитать: Рейтинг банков для малого бизнеса с выгодным РКО для ИП и ООО.

Как узнать, в какой валюте открыт счет

С помощью расшифровки разряда «333» можно узнать валюту счета организации или ИП. Чаще всего встречаются цифры:

810	рубли
840	доллары
978	евро
156	юани

Например, счет 407 02 810… оформлен негосударственной коммерческой компанией в валюте РФ.

Какой код рубля: 810 или 643 разъяснение Центробанка РФ

Все спорят, какой же код рубля: 810 или 643. Мы нашли документ на официальном сайте Центрального банка РФ, в котором все подробно разъяснено.

Зачем нужен проверочный код

Проверочный код («4») не несет смысловой нагрузки. Этот ключ нужен Центробанку, чтобы на основе специально разработанного компьютерного алгоритма проверить, правильно ли записан счет.

Как проверить, в каком отделении оформлялся счет

Блок «5555» обозначает внутренний номер филиала банка, в котором был открыт счет. Если филиалов нет, разряд заполняется нулями. Однако, по этим цифрам нельзя определить банк, зарегистрировавший счет (для этого есть БИК).

То есть сказать, что, к примеру, счет 407 01 810 0001… зарегистрирован в Сбербанке или в каком-то другом банке нельзя, можно только, заранее зная банк, узнать, в каком филиале открывался счет. Определить банк можно только по номеру карты, по номеру счета эта информация недоступна.

Что означают последние 7 цифр в счете

Последний блок «6666666» — уникальный номер счета в конкретном филиале банка. Для последовательности этих цифр нет единого стандарта, правила нумерации определяются банками самостоятельно. Обычно присваивается порядковый номер счета в конкретном банковском подразделении.

Пример. 40702 810 4 0000 0123456 — счет открыт негосударственной коммерческой организацией (40702), в рублях (810), в головном отделении (0000), номер счета в системе банка — 0123456.

Расшифровка чисел к буквам | Поиск контактной информации

Результаты листинга Расшифровка номеров в буквы

Конвертировать все :: Преобразование телефонных номеров

5 часов назад Номер телефона с на Буквы . Телефон : -. См. Примечания для разных. номер / письмо присвоения. Примечания. Вопросы и ответы были связаны с 0 и 1. Этот инструмент использует…

5 часов назад Преобразуйте телефонный номер во все буквенные комбинации . Введите номер телефона . Телефонный номер может содержать от 3 до 10 букв и чисел , разделенных пробелами, дефисами «-» или. круглые скобки «()». Если выбран вариант «Преобразовать номер телефона в слова», выберите список слов на английском или голландском языках для проверки телефонных слов. If «Преобразовать номер телефона во все буквы

3 часа назад Совет 1. Найдите легко запоминающуюся мнемонику для телефонных номеров , кодов доступа, комбинаций блокировок, PIN-кодов и т. д.Пример: 2355 — сотовый, а 8472 — VISA. Совет 2: Номера преобразуются в соответствии с клавиатурой телефона : 1 в 1; 2 к a, b или c; От 3 до d, e или f и так далее.

8 часов назад Числа с на Конвертер букв . Преобразуйте чисел в букв в различных форматах.Нумерация букв таким образом, что A = 1, B = 2 и т. Д., Является одним из простейших способов их преобразования в чисел . Это называется шифром A1Z26. Однако есть и другие варианты, такие как коды ASCII, коды ответвлений или даже периодическая таблица элементов для декодирования чисел .

Just Now Код Multi-Tap — это имя, данное для метод телефонного ввода, заключающийся в написании буквы путем повторения соответствующей клавиши на клавиатуре мобильного телефона .Например: «2» для «A», «22» для «B», «222» для «C», «3» для D и т. Д. «CODE» записывается как «222-666-3-33». . У dCode есть инструмент для этого:

2 часа назад В нижней части конвертера введите номер телефона в поле Номер телефона и нажмите кнопку «Создать Letter Pad».Появится клавиатура, содержащая букв , доступных для каждой цифры телефонного номера . Нажмите кнопку в каждом ряду, чтобы собрать цифр (комбинация букв и цифр ). Вернуться к калькулятору.

4 часа назад Многие компании сегодня суетятся с номерами .Вместо того, чтобы выдавать фактический номер , они дают вам слово номер телефона , которое произносится как «800-call-today». Это утомительно и отнимает много времени, чтобы найти эти букв на клавиатуре телефона , а затем преобразовать их в числа .

6 часов назад Расшифровать Сообщение Введите или вставьте закодированное сообщение в левое поле.Выберите правильный ключ , номера , затем нажмите « Decode », чтобы открыть скрытое сообщение. Закодированный текст. Ключ1 Ключ2.

8 часов назад Расшифровка номера телефона . Большинство людей никогда не увидят причин задаться вопросом, как и почему работает телефон; ему просто нужен гудок, и кто-то должен поднять трубку, когда набирается номер , но за условным обозначением номера стоит настоящая наука.

8 часов назад Ответ (1 из 5): Если вы посмотрите на номеров на телефоне от 2 до 9, вы увидите соответствующие букв под номерами , независимо от того, используете ли вы телефон с сенсорным или дисковым набором номера .2 (A, B, C) 3 (D, E, F) 4 (G, H, I) 5 (J, K, L) 6 (M, N, 0) 7 (P, Q, R, S) 8 (Т, У, В) 9 (Ш, Х, Y, Z). Просто наберите соответствующий номер

6 часов назад Номер телефона Cipher Solution. (Это часть ответа на Puzzle: номеров телефонов .) Вы можете закодировать имя с буквой 4-, если переставите клавиатуру следующим образом: 1 2 3 abc def ghi 4 5 6 jkl mno pqr 7 8 9 stu vwx yz * 0 #.Это позволяет кодировать 4 букв : ADRI = [(1,2,1), (8,3,6)], где первые числа каждого кортежа — это ранг объединенного

7 часов назад Base64 легко распознать. Он состоит из букв (примерно 50% прописных и 50% строчных), а также цифр и часто равных символов (=) в конце.Base64 Decoder Tool; Азбука Морзе. Код Морзе — это высоконадежный метод связи, который можно передавать разными способами даже в сложных и шумных условиях.

4 часа назад Клавиатура letter для набора номера отсутствует pad в приложении Phone .С каждым числом связано букв , то есть A, B и C представлены цифрами 2, поэтому просто введите номер , связанный с буквой , которую вы хотите ввести. букв должны быть…

3 часа назад Выберите, чтобы слова для чисел были строчными, прописными или регистр заголовка, чтобы легко скопировать и вставить в другое приложение.Этот конвертер преобразует чисел в слова и цифры в слова. Число в словах может быть выполнено для реальных чисел и Scientific E Notation. Limited…

7 часов назад Введите 6–10-значный номер телефона , и мы покажем вам, какие слова и фразы произносятся в вашем номере телефона , чтобы помочь вам решить, хотите ли вы его оставить.Выберите новый 7- или 8-значный номер телефона , введя доступный обмен (первые 3-5 цифр) и посмотрите, какие однословные номера вы можете выбрать.

8 часов назад Ответ: Нет. Ты не можешь. Из-за того, как работают коды . Код НАЗНАЧАЕТ значение данному символу, и между этими двумя вещами нет никакой связи и нет шаблона.A = 4, B = -27, C = 41/3… это код . Что означает D? Вы не узнаете, если не найдете код присвоение A …

8 часов назад Введите полный номер телефона и посмотрите, какие слова и фразы он произносит. Введите начало телефонного номера и посмотрите, какие слова начинаются с этих цифр.Введите букв и увидите (и даже наберите) соответствующий номер . Введите свой 16-значный «код друга» Wii и посмотрите, не написано ли это что-нибудь крутое. Поисковая система PhoneSpell ® предоставляет 4 услуги в одной !!

1 . Начните искать в сообщении однобуквенные слова. Большинство кодов, использующих относительно простой метод подстановки, легче всего взломать, выполнив простую настройку, вычисляя буквы одну за другой и терпеливо выясняя код на основе предположений. Однобуквенные слова в английском языке будут «я» или «а», поэтому вам следует попробовать вставить одно, ища шаблоны и, по сути, играя в палача.Если у вас есть решенный «а — -», вы знаете, что чаще всего это будет «есть» или «и». Угадай и проверь. Если это не сработает, вернитесь и попробуйте другие варианты. Будьте терпеливы и действуйте медленно. Не беспокойтесь о «взломе» кода столько, сколько о том, чтобы научиться его читать. Поиск закономерностей и распознавание правил, по которым написан английский (или любой другой язык, на котором пишется код), поможет вам решить код с некоторым временем и усилиями.
2 . Ищите наиболее часто встречающиеся символы или буквы. Чаще всего в английском языке используется буква «е», за которой следуют «т» и «а».В процессе работы используйте свое знакомство с общими словами и структурой предложений, чтобы начать делать логические предположения. Вы редко будете чувствовать себя уверенно, но в эту игру по взлому кода нужно делать логический выбор, возвращаться назад и исправлять свои ошибки. Следите за двойными символами и короткими словами и начните решать их первыми. Легче попытаться сделать обоснованное предположение относительно «дороги», «в» или «на».
3 . Ищите буквы после апострофов. Если в сообщении есть знаки препинания, вам повезло.Это предлагает целый ряд других подсказок, которые вы можете научиться распознавать. За апострофами почти всегда следует S, T, D, M, LL или RE, AR, BT. Итак, если у вас есть два одинаковых символа после апострофа, вы решили «L» или «D».
4 . попробуйте определить, какой код вы нашли. Если в процессе решения вы думаете, что узнаете один из распространенных типов кода из приведенного выше, значит, вы взломали его и можете прекратить зацикливание и заполнить сообщение на основе вашего кода.Это, вероятно, будет происходить не часто, но чем больше вы познакомитесь с общими кодами, тем более вероятно, что вы узнаете тип используемого кода и сможете его решить. Подстановки цифр и коды клавиатуры особенно распространены среди обычных повседневных секретных сообщений. Следите за ними и применяйте их по своему усмотрению.

6 часов назад Введите номер телефона (с букв ): 1800FLOWERS. Выведите номер телефона для «1800FLOWERS» — «18003569377».Follow изменено 12 дек. ответил 12 декабря Как мне прочитать / преобразовать InputStream в строку в Java? 490. Как сделать наценку номеров телефонов ? 924.
5 часов назад Cryptii. Конвертируйте, кодируйте, шифруйте, декодируйте и расшифруйте ваш контент онлайн. Внимание! Эта версия cryptii больше не находится в активной разработке.Последнюю версию можно найти на сайте cryptii.com. Cryptii — это веб-приложение с открытым исходным кодом под лицензией MIT, где…
Just Now Phonetic Alphabet Tables . Полезно для написания слов и имен по телефону . Я распечатал эту страницу, вырезал таблицу с фонетическим алфавитом НАТО (ниже) и приклеил ее к монитору компьютера, когда я работал техником службы поддержки колл-центра.Альтернативная версия, фонетический алфавит Western Union, представлена в случае, если НАТО
8 часов назад Шифр A1Z26 — преобразование букв и чисел . Преобразует алфавитные символы в их соответствующий алфавитный порядок число (e.грамм. A = 1, B = 2,…, Z = 26), а неалфавитные символы отбрасываются. Шифр Бофорта Поиск в Unicode Конвертер начальной строки Код Бодо Текст в восьмеричное число
5 часов назад Помните, что с номерами 1 и 0 не связаны букв для них; также помните, что число 0 и буква O не совпадают. Вы также можете попробовать противоположное этому калькулятору; он преобразует телефонный номер в альфа-представление.
3 часа назад Каждая клавиша на вашем телефоне соответствует 3-4 буквам . Здесь вы можете быстро найти телефонный номер (а), который соответствует данному слову, включая использование цифр в качестве псевдо букв (p53ud0 13773r5).
5 часов назад Введите десятичное число в поле для справа от десятичной точки.Введите номер в поле и нажмите «Щелкните для преобразования». Если номер равен 346 894, введите «346 894» (без кавычек). Не вводите десятичную точку. Если номер — это 2154, вы можете ввести «2,154», вы…
5 часов назад Конвертер Word в телефонный номер используется для преобразования слова в телефонный номер на основе сопоставления буквы клавиатуры международного стандарта любого мобильного телефона или стационарного телефона .Например, номер для Apple — это 27753. Если вам разрешено выбрать свой собственный телефон или мобильный номер номер , вы можете использовать этот инструмент, чтобы выбрать запоминающийся
2 часа назад Буквенные номера . Один из первых шифров, который выучили дети, — это шифр « буквенное число ».Вы заменяете букв на цифр : A = 1, B = 2, C = 3 и т. Д. При шифровании будут закодированы только букв . Не букв будут рассматриваться как пробелы. При расшифровке чисел будут заменены на букв , дефисы будут удалены, а остальные заполнители будут действовать как пробелы.
2 часа назад К счастью, есть стандарт (ITU E.161, также известный как ANSI T1.703-1995 / 1999 и ISO / IEC 9995-8: 1994), и большинство современных телефонов помещают букв на клавиатуре phone в соответствии с этим стандартом. В следующей таблице показано, как наиболее часто используются прикосновения…
5 часов назад Переводчик кода Морзе это переводчик, который позволяет любому переводить текст в азбуку Морзе и легко декодировать код Морзе в текст.С помощью онлайн-переводчика кода Морзе любой может преобразовать любой простой текст на английском или другом языке в код Морзе и наоборот.
8 часов назад Буква Комбинации телефонного номера . Середина. 7742 590 Добавить в список Поделиться. Учитывая строку, содержащую цифры от 2 до 9 включительно, верните все возможные комбинации букв , которые может представлять число .Верните ответ в любом порядке. Ниже приведено сопоставление цифры букв (как и на кнопках телефона). Обратите внимание, что 1 не соответствует
5 часов назад Наш телефонный номер переводчик делает именно это. Вы говорите, что введите номер телефона , содержащий буквы , и сообщите ему, какую клавиатуру телефона вы хотите использовать, и он переведет букв в номеров .Он также сообщит вам, переводятся ли слова на разные номера на различных телефонных клавиатурах .
2 часа назад Сообщение, содержащее букв из AZ, можно закодировать в цифр используя следующее отображение: ‘A’ -> «1» ‘B’ -> «2» ‘Z’ -> «26» Чтобы декодировал закодированное сообщение, все цифры должны быть сгруппированы, а затем преобразованы обратно в букв используя отображение, обратное приведенному выше (может быть несколько способов).Например, «11106» можно отобразить в: «AAJF» с группировкой (1 1 10 6)
5 часов назад 1. Преобразование числа в букв в верхнем регистре. Верхний регистр букв Диапазон значений ASCII начинается от 65 до 90. Мы используем цикл for, который начинается со значения 65, равного , буквы A и так далее, и заканчивается значением 90, равным , буква Z.Метод javascript fromCharCode () изменяет значение num на charcater и добавляет к Str. После завершения цикла мы печатаем результат, используя
2 часа назад Начните с ввода 7-значного телефонного номера . Однако при преобразовании 7-значного числа в , например 266-7883, вы обнаружите, что значительно быстрее сначала преобразовать 266-0000, а затем преобразовать 000-7883.Введите нули в 3- или 4-значную область, которую вы НЕ преобразовываете. Время, затрачиваемое на альфа-поиск
8 часов назад Конвертер чисел из в текст / слов. Онлайн-калькулятор конвертации, позволяющий конвертировать любое число в текстовый (или) формат слов.Например: если вы введете любое число (положительное, отрицательное или десятичное), вы получите текст / слово в формате данного числа .
9 часов назад Это особенно актуально, если вы хотите проверить несколько телефонных номеров (вам нужно выполнить это преобразование только один раз).Фактически, вы можете полностью предварительно вычислить это, используя сопоставление словаря из телефонных номеров ко всем (четыре букв ) слов в словаре.
2 часа назад Инструмент для взлома кода. Этот инструмент можно использовать как инструмент, который поможет вам декодировать многие методы шифрования.Он не сделает всю работу за вас, но может легко декодировать коды ROT13 и помочь вам взломать шифры подстановки. Это очень полезно для декодирования некоторых сообщений, найденных во время геокэшинга! Хороший пример взлома пароля
5 часов назад Письма на Телефонный номер . Телефонные номера в США могут содержать букв , особенно бесплатные телефонных номеров . Если вы посмотрите на панель телефона , вы увидите, что каждое число соответствует 3 буквам . Просто нажмите номер , где появится буква ; например, 1.800.AUPAIRS будет 1.800.287.2477. SIM-карты
3 часа назад Это позволит вам набрать букв вместо номера .Затем наберите букв в телефонном номере . Например, наберите B-E-S-T-B-U-Y, и телефон автоматически расшифрует чисел , которые букв должны представлять. Нажмите зеленую кнопку и вы набираете номер!
3 часа назад Распечатать все возможные слова из телефонных цифр .До появления QWERTY-клавиатур текстов и номеров размещались на одной и той же клавише. Например, у 2 есть «ABC», если мы хотим написать что-либо, начинающееся с «A», нам нужно ввести ключ 2 один раз. Если мы хотим ввести «B», нажмите клавишу 2 дважды и трижды, чтобы ввести «C». Ниже представлено изображение таких
7 часов назад Выше показаны результаты расшифровки .Используя генератор слов и средство расшифровки слов для букв D E C I P H E R , мы расшифровали букв , чтобы создать список всех слов, найденных в Scrabble, Words with Friends и Text Twist. Всего найдено 137…
Важные примечания:
* = 700-728 выдача этих номеров железнодорожным служащим была прекращена 1 июля 1963 года.
Если один и тот же номер области появляется выше более одного раза, это потому, что определенные номера были переданы из одного штата в другой или что номер области был разделен для использования между определенными географическими точками.
Любой номер, начинающийся с «000», «666», «900-999», имеющий в середине «00» или оканчивающийся на «0000», никогда не будет действительным SSN.
Первоначально первые три цифры присваивались географическим регионом, в котором человек проживал в момент присвоения номера.«Обычно номера присваивались, начиная с северо-востока и двигались на запад. Таким образом, люди на восточном побережье имели самые низкие номера, а люди на западном побережье — самые высокие».
С 1972/1973 года, когда SSA начало назначать SSN и выдавать карты централизованно из Балтимора, присвоенный номер района основывался на почтовом индексе в почтовом адресе, указанном в заявлении на получение исходной карты социального обеспечения. Почтовый адрес заявителя не обязательно должен совпадать с местом его рождения или проживания.До 1972/1973 годов номера социального страхования присваивались местными отделениями. Таким образом, номер района не обязательно отражает государство проживания заявителя до 1972/1973 года или после него.
Люди, родившиеся в Соединенных Штатах с 1987 года, могли получить SSN при рождении в больнице. Эта политика зависит от штата.
Начиная с 25 июня 2011 года, SSA начало новую методологию рандомизированного назначения, названную «Рандомизация SSN», чтобы продлить срок службы девятизначного SSN по всей стране, а также в целях безопасности, поскольку рандомизация затрудняет получение недавно назначенного SSN. реконструировать с использованием общедоступной информации.Неиспользуемые номера областей, ранее назначенные штатам, а также ранее не назначенные номера областей теперь будут доступны в новой системе рандомизации.
Первоначально этим состояниям были присвоены номера
, выделенные красным, но впоследствии не были присвоены в июне 2011 года и использовались в новом рандомизированном назначении. Номера в этих «официально» невыпущенных сериях, возможно, все еще были выданы заявителям в этих штатах до рандомизации.
Номера социального страхования никогда не меняются после смерти человека.Несмотря на то, что с 1936 года было выпущено более 450 миллионов SSN и присвоено около 5,5 миллионов новых номеров в год, они все еще могут выдавать новые номера для нескольких поколений.
Первоисточник: www.socialsecurity.gov. Все данные актуальны по состоянию на 15 апреля 2019 года.
Код Морзе — это схема кодирования символов, которая позволяет операторам отправлять сообщения, используя серию электрических импульсов, представленных другими словами в виде коротких или длинных импульсов, точек и тире.
Сэмюэл Морс получил патент США, US1647A, на телеграфные сигналы с точечным тире 20 июня 1840 года. С другой стороны, некоторые источники утверждают, что Сэмюэл Морс получил патент на азбуку Морзе, выданный османским султаном Абдулмеджидом I.Однако, согласно мемуарам Сайруса Хэмлина и некрологу The New York Times, опубликованному 3 апреля 1872 года, Сэмюэл Морс вместо этого получил не патент, а орден Османской империи — Орден Славы.
В прошлом азбука Морзе широко использовалась, особенно в вооруженных силах.Хотя сегодня азбука Морзе имеет ограниченную область применения, она все еще используется в авиации, радиолюбительской деятельности и вспомогательных технологиях (AT).
Код Морзе
можно использовать по-разному, например, с помощью ручки и бумаги или с помощью света и звука. Даже его можно использовать с такими частями тела, как глаза или пальцы.
Трудно ли выучить азбуку Морзе?
Несмотря на то, что в прошлом азбука Морзе требовала сложного обучения, благодаря современным приложениям, таким как переводчик кода Морзе или клавиатура Gboard, в настоящее время выучить азбуку Морзе стало проще.
Как выучить азбуку Морзе?
Вы можете выучить азбуку Морзе, изучая и слушая азбуку Морзе, а также используя техники запоминания слов, которые можно найти на различных веб-сайтах. Однако одним из лучших методов обучения азбуке Морзе в 2021 году станет клавиатура Gboard, разработанная Google. С помощью упражнений для изучения Морзе, предоставленных Google Creative Lab, вы даже можете выполнять упражнения онлайн бесплатно.
Как читать азбуку Морзе?
Если вы недостаточно хорошо читаете азбуку Морзе, вы можете найти соответствующее представление Морзе каждого символа из таблицы азбуки Морзе или воспользоваться переводчиком азбуки Морзе.
Как перевести код Морзе?
Если вы хотите перевести или расшифровать азбуку Морзе и не умеете читать азбуку Морзе, вы можете воспользоваться переводчиком азбуки Морзе онлайн. С помощью декодера Морзе вы можете легко декодировать азбуку Морзе и читать английский текст. Поэтому можно и закончить поиск вопросом, как вы переводите азбуку Морзе.
Что такое переводчик азбуки Морзе?
Morse Code Translator — это переводчик, который позволяет любому переводить текст в азбуку Морзе и легко декодировать азбуку Морзе в текст.С помощью онлайн-переводчика кода Морзе любой может преобразовать любой простой текст на английском или другом языке в код Морзе и наоборот.
Как пользоваться переводчиком азбуки Морзе?
Просто введите азбуку Морзе или текст в соответствующие поля ввода, чтобы использовать преобразователь кода Морзе. Например, вы помните SMS-сигнал Nokia? Попробуйте расшифровать «… — …», а затем воспроизвести его звук. Как насчет расшифровки секретного сообщения на азбуке Морзе или пасхального яйца, которое вы нашли в игре, в которую вы играли? Что ж, переводчик азбуки Морзе может помочь вам, если у вас есть подключение к Интернету и вы хотите выучить азбуку Морзе.
Что означает SOS?
SOS — это сигнал бедствия на азбуке Морзе, признанный во всем мире для получения помощи. Впервые он был принят правительством Германии в 1905 году. Хотя некоторые люди думают, что SOS означает «Спасите наши души» или «Спасите наш корабль», его буквы ничего не означают.
Что такое SOS в азбуке Морзе?
SOS на азбуке Морзе — «… — …»
Что такое азбука Морзе для «Я люблю тебя»?
«Я люблю тебя» на азбуке Морзе — «.. / .- .. — …-. / -.— — ..- ”
Как поздороваться на азбуке Морзе?
«Привет» на азбуке Морзе — «….. .- .. .- .. — »
Как сказать «помощь» на азбуке Морзе?
«Справка» на языке Морзе — «….. .- .. .—. », Но вы также можете использовать сигнал SOS, который представляет собой« … — … ».
Что означает — в азбуке Морзе?
«—» означает «O» на азбуке Морзе.
Что означают 3 точки в азбуке Морзе?
Буква S — это три точки в азбуке Морзе: «… »
Может ли Siri перевести код Морзе?
Да, Siri может переводить азбуку Морзе. Если вы хотите попробовать, скажите: «Привет, Siri, что такое азбука Морзе для Hello?»
Преобразователь римских цифр
Использование калькулятора
Преобразование римских цифр в числа и преобразование чисел в римские цифры.
Используйте этот преобразователь римских цифр для преобразования чисел от 1 до 3 999 999 в римские цифры.Или введите римскую цифру, чтобы получить ее обычное арабское значение.
Римские цифры — это система счисления, разработанная в Древнем Риме, где буквы обозначают числа. Современное использование римских цифр включает буквы I, V, X, L, C, D и M.
Для преобразования римских цифр больше 3999 используйте приведенную ниже таблицу для входов преобразователя. Используйте начальный символ подчеркивания для ввода римских цифр с чертой. Линия над римской цифрой означает, что она умножена на 1000.
Например,
C = 100 000. Входить C в конвертер как _C.
СМ =
0. Входить CM в конвертер как _C_M.
Наибольшее число, которое вы можете написать римскими цифрами, — 3,999, что соответствует MMMCMXCIX. Вы можете представить числа, превышающие 3999, римскими цифрами, используя верхнюю черту. Верхняя черта над римской цифрой означает, что вы умножаете эту римскую цифру на 1000.Для числа 50 000 римскими цифрами вы должны использовать римскую цифру L (50) с верхней чертой, чтобы получилось 50 000.
Например, L означает 50 × 1000 = 50000. Чтобы ввести 50 000 в этот калькулятор в виде римской цифры, введите _L.
Сопутствующие калькуляторы
Конвертер римских цифр позволяет преобразовывать даты в римские цифры или римские цифры в числовые даты.
Калькулятор римских цифр позволяет выполнять базовые математические операции с римскими цифрами.
Как расшифровать номер социального страхования
Как расшифровать номер социального страхования
Кредит изображения: marcusamelia / iStock / GettyImages
То, что ваш номер социального страхования говорит о вас, зависит от того, когда вам был выдан номер.Девять цифр, составляющих каждый уникальный номер, всегда делились на трехзначный номер области, двухзначный групповой номер и четырехзначный серийный номер. До середины 2011 года номер социального страхования использовался для идентификации как штата выдачи, так и приблизительного времени выдачи карты. Однако с 25 июня 2011 года действует процесс генерации случайных чисел, который защищает вашу личность и обеспечивает целостность номеров социального страхования в целом.
Номер площади
Первые три цифры номера социального страхования ранее указывали на штат , в котором этому номеру был присвоен номер .Например, первые три цифры номера, выданного в Огайо до 25 июня 2011 года, находятся в диапазоне от 268 до 302, а первые три цифры номера, выпущенного в Висконсине, находятся в диапазоне от 387 до 399.
Во избежание проблем с нехваткой номеров, номера групп областей, созданные после середины 2011 года, берутся из объединенного пула невыпущенных номеров.
Номер группы
До рандомизации номер группы позволял обнаружить недействительный или поддельный номер социального страхования.
Двухзначные номера групп варьировались от 01 до 99 и распределялись по определенному зигзагообразному шаблону. Шаблон начинался с нечетных чисел от 01 до 09, затем четных чисел от 10 до 98, четных чисел от 02 до 08 и, наконец, нечетных чисел от 11 до 99. Согласно этому шаблону номер социального страхования с 09 в качестве номера группы был выдан задолго до номера 97.
Несмотря на то, что это не надежный метод обнаружения, сравнение номера группы с самым последним списком высоких групп Администрации социального обеспечения, обновляемым ежемесячно до июня 2011 года, может предупредить работодателя или другое заинтересованное лицо о потенциально недействительном номере социального страхования.Например, пожилой взрослый, представляющий номер, в котором средние цифры 89, может содержать поддельный номер, потому что нечетные числа от 11 до 99 были одними из последних, выпущенных в 2011 году.
Серийный номер
Последняя группа цифр не имела особого значения, кроме как дополнительной меры для обеспечения уникальности каждого выданного номера. Серийные номера от 0001 до 9999 были присвоены в последовательном порядке.
Как расшифровать ваши числа холестерина
HDL слишком низкий? ЛПНП слишком высокий? А что такое триглицериды? Если вы когда-либо были сбиты с толку своими показателями холестерина, вы не одиноки.
Холестерин — это ключевой показатель циркулирующих в крови жиров. Он получил плохую репутацию, но некоторое количество холестерина важно для правильного функционирования вашего тела.
Однако слишком высокий уровень холестерина подвергает ваше тело риску серьезных заболеваний.
Почему так важны анализы на холестерин
Результаты вашего теста на холестерин важны, потому что они показывают, есть ли у вас риск атеросклероза, накопления налета на стенках артерий.
Обследование особенно важно, потому что высокий уровень холестерина часто протекает бессимптомно.
Действительно ли одни значения холестерина важнее других?
Когда вы проходите обследование на холестерин, ваш врач проверит уровень общего холестерина, липопротеинов низкой плотности (ЛПНП), липопротеинов высокой плотности (ЛПВП) и триглицеридов.
Врачи считают, что общий холестерин превышает соотношение ЛПВП. В идеале число меньше 3.
Вот более подробная разбивка идеальных значений холестерина:
Общий холестерин: Менее 200 мг / дл.
ЛПВП или «хороший» холестерин: 60 мг / дл и выше. ЛПВП связывается с плохим холестерином в артериях и переносит его в печень, где он может быть переработан. Более высокий уровень ЛПВП снижает риск сердечных заболеваний.
ЛПНП или «плохой» холестерин: Менее 100 мг / дл. ЛПНП накапливаются на стенках кровеносных сосудов, что приводит к затвердеванию и сужению артерий, закупорке и повышенному риску сердечных заболеваний.
Триглицериды: Менее 100 мг / дл.Триглицериды — это тип жира в крови, который используется организмом для получения энергии. Однако высокий уровень триглицеридов может быть признаком метаболического синдрома и подвергать вас риску сердечных заболеваний. Высокий уровень триглицеридов обычно является результатом диеты с высоким содержанием насыщенных и трансжиров, недостатка физических упражнений и / или ожирения. Регулярные упражнения и поддержание здорового веса обычно значительно снижают уровень триглицеридов.
Изменения образа жизни для снижения холестерина
Изменения образа жизни, такие как диета с низким содержанием жиров и регулярные физические упражнения, могут существенно повлиять на снижение холестерина, но некоторым людям нужны лекарства для борьбы с высоким уровнем холестерина.
Эта тактика может помочь снизить уровень холестерина:
Бросить курить.
Следите за уровнем сахара в крови, особенно если вы диабетик.
Регулярно занимайтесь спортом.
Избавьтесь от стресса. Ситуации высокого стресса могут повысить ваше кровяное давление (еще больше увеличивая риск сердечных заболеваний) и могут побудить вас переесть жирную пищу, что повышает уровень холестерина ЛПНП.
Следите за своим весом. Похудение может как повысить, так и снизить ЛПНП.
Придерживайтесь здоровой диеты с низким содержанием насыщенных и трансжиров.
Основывайте свои блюда на свежих овощах, фруктах и цельнозерновых продуктах.
Выбирайте нежирные или обезжиренные молочные продукты.
Ограничьте употребление красного мяса.
Ешьте рыбу не реже двух раз в неделю.
Уменьшите потребление натрия.
Избегайте сладких напитков.
Поговорите со своим лечащим врачом о своем уровне холестерина — знание своих цифр может спасти вам жизнь.
Или запишитесь на прием к кардиологу в Пьемонте.
История социального обеспечения
Схема нумерации SSN
Номер состоит из трех частей
Девятизначный SSN состоит из трех частей:
Первый набор из трех цифр называется областью . Число
Второй набор из двух цифр называется группой . Число
Последний набор из четырех цифр — Serial Число
Номер участка
Номер зоны присваивается географическим регионом.До 1972 г., карты были выпущены в местных отделениях социального обеспечения в окрестностях г. страна и номер района представляли штат, в котором карта была выпущена. Это не обязательно должно быть государство, в котором заявитель жил, так как человек мог подать заявление на получение карты в любой офис социального обеспечения. С 1972 года, когда SSA начала назначать SSN и выдача карт централизованно из Балтимора, региональный номер присвоено было основано на почтовом индексе в предоставленном почтовом адресе в заявлении на получение оригинальной карточки социального страхования.Заявитель почтовый адрес не обязательно должен совпадать с местом жительства. Таким образом, номер области не обязательно отражает состояние место жительства заявителя до 1972 года или после.
Как правило, номера присваивались, начиная с северо-востока и движется на запад. Таким образом, у людей на восточном побережье самые низкие цифры а на западном побережье больше всего.
Примечание: не следует слишком сильно относиться к «географическому положению». код «. Он не предназначен для использования в качестве географического Информация. Схема нумерации была разработана в 1936 году (до ЭВМ). чтобы SSA было проще хранить приложения в наших файлах в Балтиморе, поскольку файлы были организованы по регионам, а также по алфавиту. На самом деле это было просто бухгалтерское устройство для наших собственное внутреннее использование и никогда не предназначалось для чего-то большего, чем что.
Номер группы
В каждой области диапазон номеров группы (две (2) средние цифры) от 01 до 99, но не назначаются последовательно. Для административных причины, номера групп, выданные первыми, состоят из НЕЧЕТНЫХ номеров из 01–09, а затем ЧЕТНЫЕ числа от 10 до 98 в каждом номер области, выделенный государству. Ведь номера в группе 98 определенной области были выпущены, ЧЕТЫЕ группы 02 — 08, за которыми следуют группы ODD с 11 по 99.
Номера групп присваиваются следующим образом:
НЕЧЕТНЫЙ — 01, 03, 05, 07, 09 —— ЧЕТНЫЙ — 10 до 98
ЧЕТНЫЙ — 02, 04, 06, 08 —— НЕЧЕТНЫЙ — от 11 до 99
Посмотреть последние Ежемесячная таблица выдачи номеров социального страхования для последнего SSN диапазоны площадей, выданные на сегодняшний день.