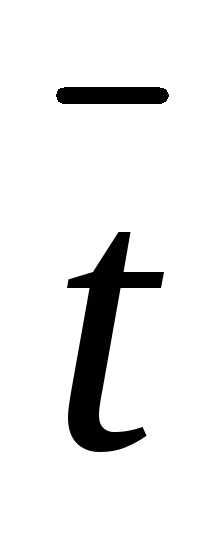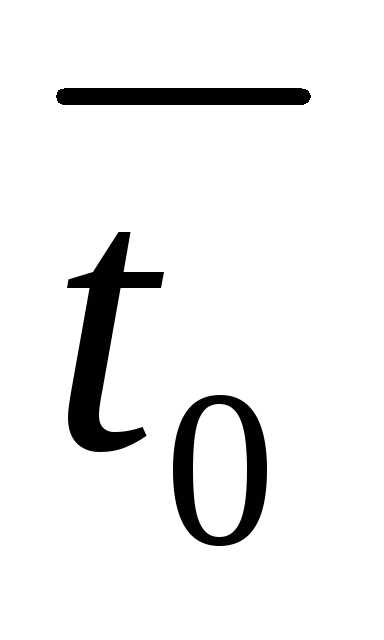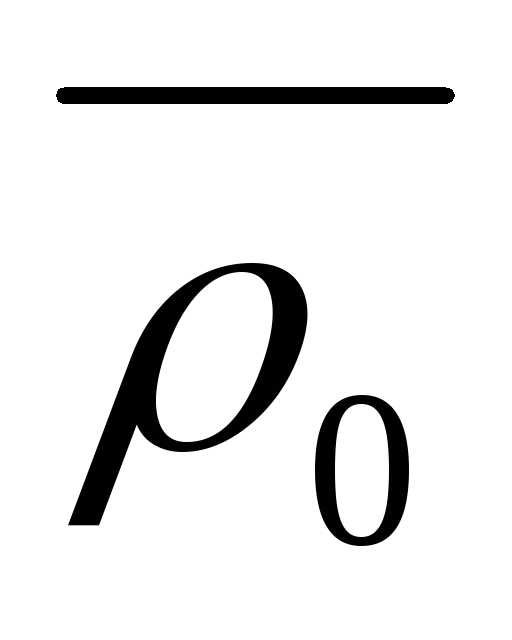Зависимость вязкости от температуры —
С повышением температуры вязкость капельных жидкостей и их смесей понижается.
Математических уравнений, пригодных для практического применения, выражающих закон изменения вязкости от температуры, до настоящего времени не имеется, поэтому пользуются эмпирическими зависимостями. Для минеральных масел с вязкостью > 80 ccm при температурах от 30 до 1500 С пользуются выражением
где и – кинематические коэффициенты вязкости при заданной температуре t и температуре 500 С в ccm;
n – показатель степени, значения которого в зависимости от исходной вязкости при 500 С приведены ниже.
| Вязкость | 2,8 | 6,25 | 9,0 | 11,8 | 21,2 | 29,3 |
| Показатель n | 1,39 | 1,59 | 1,72 | 1,79 | 1,99 | 2,13 |
| Вязкость | 37,3 | 45,1 | 52,9 | 60,6 | 68,4 | 80,0 |
| Показатель n | 2,24 | 2,32 | 2,42 | 2,49 | 2,52 | 2,56 |
В гидросистемах применяются жидкости, вязкость которых при 500 С составляет 10-100 спз. В частности вязкость применяемого в самолетных гидросистемах масла АМГ – 10 при 500 С равна 10 ccm.
Зависимость вязкости распространенных масел от температуры показана на рис. 2. а и б. Очевидно, чем меньше изменяется вязкость с изменением температуры, тем выше качество и лучше эксплуатационные свойства рабочей жидкости. При применении жидкостей, имеющих крутую кривую температурной зависимости вязкости, затруднена работа гидросистемы в зимних условиях эксплуатации.
Обычно вязкостно – температурные свойства жидкостей характеризуются отношением Жидкость, предназначенная для эксплуатации в широком температурном интервале, считается пригодной, если ее вязкость при изменении температуры от – 500 С до + 500 С изменяется не более, чем в 100 раз.
Рис. 2. Графики зависимости динамической вязкости
масел от температуры:
1 – трансформаторное; 2 – индустриальное 12;
3- индустриальное 20; 4 – индустриальное 30;
5- индустриальное 50; 6- автотракторное;
7- МВП; 8- ЦИАТИМ-1; 9- АМГ-10
einsteins.ru
Исследование зависимости вязкости моторного масла от температуры
Томск — это город, в котором зима бывает очень суровой. И ежегодно среди автомобилистов возникает проблема сложного, а порой и невозможного, запуска двигателя автомобиля в зимних условиях. Эта проблема может возникнуть по ряду причин. Когда двигатель холодный, наоборот, масло обладает тенденцией сгущаться. И, как следствие, невозможность прокрутки вала двигателя. Моторное масло играет важнейшую роль в эксплуатации двигателя автомобиля. Его основная задача — это смазка. Моторное масло разных видов и сортов отличается по характеристикам, определяющим сферу их применения. В зависимости от характеристик, масло рекомендуется для использования в разных типах двигателей, работающих в различных условиях и температурных режимах. Для покупателей наибольшую важность представляют два показателя: вязкость (позволяет определить, подойдет ли масло для определенного сезона и климата) и допуск (подходит ли масло для данного автомобиля). Причем даже для одного и того же типа масла, но разных марок показатель вязкости может отличаться в зависимости от температурных условий. Исходя из этого, нами была поставлена следующая
Для реализации поставленной цели решались следующие задачи:
- Изучить классификацию моторных масел;
- Изучить характеристики моторных масел;
- Определить вязкость моторных масел при различных (низких) температурах;
- Сформулировать рекомендации автомобилистам по применению различных масел при низких температурах.
Объект исследования: моторное масло.
Предмет исследования: вязкость.
Методы исследования.
Теоретические: анализ информации по темам “Моторные масла”, “Характеристики моторных масел”, “Вязкость и способы ее измерения”.
Практические: эксперимент по определению вязкости (кинематической и динамической) моторных масел при различных температурах.
В ходе исследования были получены следующие результаты.
Моторное масло — это смазочный материал, который используется с целью уменьшения трения в движущихся частях двигателей внутреннего сгорания.
Первое в мире моторное масло было запатентовано в 1873 году американским доктором Джоном Эллисом. В 1866 году Эллис изучал свойства сырой нефти в медицинских целях, но обнаружил, что сырая нефть обладает хорошими смазочными свойствами. Джон Эллис зарегистрировал Valvoline — первый в мире бренд моторного масла.
Моторное масло разделяется на три типа: минеральное, синтетическое и полусинтетическое.
Существует классификация масел по вязкостно-температурным свойствам и классификация масел по эксплуатационным свойствам (назначению и качеству). В настоящее время единственной признанной во всем мире системой классификации транспортных масел по вязкости является спецификация SAE (Американская ассоциация автомобильных инженеров).
Норма SAE J 300 определяет степень вязкости для каждого смазочного материала.
SAE J-300 содержит 6 зимних классов и 5 летних классов моторных масел.
Классы вязкости SAE OW, 5W, 10W, 15W, 20W, 25W относятся к зимним, а SAE 20, 30, 40, 50, 60 — к летним.
Надежность работы двигателя во многом определяется выбором масла с оптимальной вязкостью.
Вязкость — это одна из важнейших характеристик масел, которая характеризует внутреннее трение, определяет текучесть и способность обеспечить жидкостной режим смазывания. Различают кинематическую и динамическую вязкость.
Кинематическая вязкость, характерная для простых масел при положительных температурах, определяется в капиллярных вискозиметрах, а динамическая — для загущенных (всесезонных) масел и масел при отрицательных температурах, определяется в ротационных вискозиметрах, ее величина зависит не только от температуры, но и от градиента скорости сдвига.
Динамическую вязкость представляет собой произведение кинематической вязкости на плотность жидкости, в технической системе ее измеряют в сантипуазах (сП), а в системе СИ — в миллиПаскаль-секундах (мПа-с), где 1 сП= 1 мПа-с. Это сопротивление, которое оказывает жидкость при относительном перемещении двух ее слоев поверхностью 1 м
Кинематическую вязкость в технической системе единиц измеряют в Стоксах (Ст) или сантистоксах (сСт), а в системе СИ в м2/с или в мм2/с. Кинематической вязкостью [ν] называется величина, равная отношению динамической вязкости жидкости [μ] к ее плотности [ρ] при той же температуре: ν = μ/ρ.
В ходе эксперимента была измерена динамическая (методом Стокса) и кинематическая (вискозиметром ВПЖ-2, d=1,77 мм) вязкость при различных температурах для следующих марок масла:
- ZIC XQ 5w40
- Helix HX7 5w40
- Castrol Magnatec 5w40
Кинематическая вязкость определялась по следующей формуле:
K — постоянная вискозиметра (1,022 )
T — время истечения жидкости, с
ν — кинематическая вязкость жидкости, мм2/с
g — ускорение свободного падения (м/с2)
Результаты измерений показаны в таблице 1.
Таблица 1. Кинематическая вязкость (вискозиметр)
|
Масло |
t = +210С |
t = -70С |
t = -140C |
t = -180C |
t = -210 |
|||||
|
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
|
|
ZIC XQ 5w40 |
143 |
146,04 |
153 |
156,25 |
192 |
196,08 |
198 |
202,21 |
241 |
246,13 |
|
Helix HX7 5w40 |
139 |
141,957 |
188 |
191,99 |
199 |
203,23 |
224 |
228,76 |
|
251,24 |
|
Castrol Magnatec 5w40 |
128 |
130,723 |
176 |
179,74 |
230 |
234,89 |
236 |
241,02 |
239 |
244,08 |
Таким образом, можно сделать следующие выводы: 1) вязкость масла увеличивается с понижением температуры; 2) Из всех марок масел меньше всего увеличилась вязкость Castrol Magnatec.
Динамическая вязкость (Па*с) определялась по следующей формуле:
t – время падения, с
r – радиус шарика, м
R0– радиус сосуда, м
l – высота падения, м
ρ – плотность шарика, кг/м3
ρ0 – плотность жидкости, кг/м3
Для измерения вязкости использовалась следующая установка (рис. 1).
Значения динамической вязкости представлены в таблице 2.
ρ = 8900 кг/м3
l = 0,14 м
r = 2 мм
R0 = 0,015 м
Значения плотности масел:
Плотность масла ZIC XQ (при всех температурах): 1660 кг/м3.
Плотность масел Helix HX7 и Castrol Magnatec (при всех температурах): 1760 кг/м3.
Таблица 2. Динамическая вязкость (метод Стокса)
|
Масло |
t = +210С |
t = -70С |
t = -140C |
t = -180C |
t = -210C |
|||||
|
, cм/с |
μ, Па·с |
, cм/с |
μ, Па·с |
, cм/с |
μ, Па·с |
, см/с |
μ, Па·с |
, см/с |
μ, Па·с |
|
|
ZIC XQ 5w40 |
4,59 |
0,503 |
9,59 |
0,838 |
11,13 |
1,07 |
15,01 |
1,109 |
17,65 |
1,305 |
|
Helix HX7 5w40 |
1,73 |
0,34 |
4,83 |
0,81 |
7,53 |
0,996 |
10,35 |
1,505 |
13,12 |
2,103 |
|
Castrol Magnatec 5w40 |
2,56 |
0,34 |
6,36 |
0,76 |
9,48 |
0,859 |
12,15 |
1,370 |
15,95 |
2,59 |
Таким образом, можно сделать вывод, что при понижении температуры динамическая вязкость увеличивается. Причем у масла Castrol Magnatec интенсивнее, чем у ZIC и Helix.
Динамическая вязкость важна при определении низкотемпературных свойств смазок, но её редко применяют при анализе масла или для определения класса вязкости. По многим разным причинам, исследователя масла интересует кинематическая вязкость. А по этому показателю лучшие свойства показало масло Castrol Magnatec. Но сказать, что остальные масла более худшего качества нельзя. Их показатели вязкости незначительно отличаются от Castrol Magnatec и все значения укладываются в рамки допустимых производителем.
Следует отметить, что эффективность работы мотора зависит не от абсолютного значения вязкости при определенных температурах, а от динамики ее изменений при работе в определенных диапазонах рабочих температур, а также соответствие этой динамики конструкции данного двигателя. Если двигатель рассчитан на параметры авто-масла 5w30, тогда моторное масло с маркировкой 0w20 не подходит и его заливать нельзя, а с маркировкой 5w40 не рекомендуется. Значит, использовать то авто-масло, которое подходит согласно требованиям производителя двигателя, но ни в коем случае не рекомендациям изготовителя авто-масла.
В целом по маслам можно дать следующие рекомендации:
− перечень марок масел, допущенных к применению, постоянно изменяется, получают допуск новые марки, некоторые его теряют;
− температурный диапазон применения, указанный на упаковке масла, носит лишь рекомендательный характер;
− не стоит оценивать масла по цвету, большинство вводимых в него присадок делают его более темным;
− замену масла при тяжелых условиях эксплуатации необходимо производить в 1,5—2 раза чаще, тоже рекомендуется делать для автомобилей со значительным пробегом, так как условия его работы в изношенных двигателях более жесткие, в частности из-за окисляющего действия сгоревших газов, попадающих в масляный катер;
− быстрое (через 1—2 тыс. км пробега) почернение масла не обязательно указывает на потерю его эксплуатационных свойств;
− доливать следует тот же сорт масла, который залит в двигатель, так как масла разных производителей содержат различные пакеты присадок и смешивание может ухудшить их свойства;
− нежелательно смешивать минеральные и синтетические масла, а также доливать минеральное в полусинтетическое из-за разной растворимости присадок в минеральной и синтетической основах;
− если неизвестно, что использовал прежний владелец автомобиля, перед заменой желательно промыть систему смазки;
− добавление в моторное масло различных препаратов может улучшить одни его свойства и резко ухудшить другие.
e-koncept.ru
Таблицы вязкости, плотности нефтепродуктов
Сводная таблица кинематическая вязкости нефтепродуктов
| Жидкость | Температура | Кинематическая вязкость, сСт |
|---|---|---|
| Анилин | 20 | 4,3 |
| Бензин | 15 | 0,65 |
| Бензол | 20 | 0,07 |
| Глицерин 50% водный раствор | 20 | 6 |
| Глицерин 86% водный раствор | 20 | 105 |
| Глицерин безводный | 20 | 870 |
| Керосин | 15 | 2,7 |
| Нефть легкая | 18 | 25 |
| Нефть тяжелая | 18 | 140 |
| Скипидар | 16 | 1,83 |
| Спирт этиловый | 20 | 2,54 |
| Дизельное топливо (ГОСТ 305-82) | 20 | 18 — 60 |
| Масло авиационное МС, МК (ГОСТ 21743-76) | 100 | 14 – 22 |
| Масло веретенное АУ (ГОСТ 1642-75) | 20 | 49 |
| Масло индустриальное (ГОСТ 20799-75): | — | — |
| И-5А | 50 | 4 |
| И-8А | 50 | 7 |
| И-12А | 50 | 12 |
| И-25А | 50 | 25 |
| И-30А | 50 | 30 |
| И-40А | 50 | 40 |
| И-70А | 50 | 70 |
| И-100А | 50 | 100 |
| Касторовое масло | 20 | 1002 |
| Турбинное масло (ГОСТ 32-74, ГОСТ 9972-74): | — | — |
| ТП-30 | 50 | 30 |
| ТП-46 | 50 | 46 |
График зависимости кинематической вязкости мазута ГОСТ 10585-75 от температуры
Сводная таблица плотности нефтепродуктов
| Жидкость | Температура | Плотность, кг/м3 |
|---|---|---|
| Анилин | 20 | 1021 |
| Бензин | 20 | 710 |
| Бензол | 20 | 880 |
| Глицерин | 20 | 1260 |
| Керосин | 20 | 780 |
| Мазут | 20 | 740 – 1000 |
| Нефть | 20 | 730 — 1060 |
| Спирт этиловый | 20 | 790 |
| Дизельное топливо (ГОСТ 305-82) | 20 | 830 |
Плотность нефти в зависимости от температуры
Вязкость нефтепродуктов
Первая группа. Маловязкие нефтепродукты (ВУ50 — до 3 град.)
— дизельные топлива: Л, З, С и А, масла: соляровое, веретенное, трансформаторное, индустриальное, парфюмерное, приборное МВП.
Вторая группа. Нефтепродукты средней вязкости (ВУ50 — от 3 до 7 град.)
— масло осевое, моторное топливо ДТ, масло вазелиновое медицинское, цилиндровое 2, гипоидное, масло компрессорное М, мазут флотский Ф5
Третья группа. Вязкие нефтепродукты (ВУ50 — от 7 до 10 град.)
— компрессорное Т, КС-13, масла трансмиссионные автотракторные: ТАп15, Тап10, мазут флотский 12, масла авиационные, масла автотракторные: Сап10, Акп10, моторное Т, дизельные масла, вазелиновое, масла индустриальные: И-8А, И-12А, ИГП-4, ИГП-6, ИГП-8.
Четвертая группа. Высоковязкие нефтепродукты (ВУ50 — от 10 и выше град.)
— сырые нефти, мазуты топочные: 40, 100, масло цилиндровое 6, вискозин, вапор, полугудрон, топливо для мартеновских печей МП, автол АК-15, масла для холодильных машин, масла индустриальные: И-20А, И-25А, И-30А, И-40А, И-50А, И-70А, И-100А, ИГП-18, ИГП-30, ИГП-38, ИГП-49, ИГП-72, ИГП-91, ИГП-114, масла турбинные и др.
Таблица перевода в единицы СИ
Таблица 1 – Таблица перевода давления
| Паскаль, (Н/) Па | Бар, бар | Метры водяного столба, м h3O | Техническая атмосфера, (кгс/) ат | Стандартная атмосфера, атм | Тор (0°С), мм ртутного столба | Фунт силы на кв. дюйм (фунт/ ) | |
|---|---|---|---|---|---|---|---|
| 1 Па | 1 | 1,020 * | 1,020 * | 9,869 * | 7,5 * | 1,450 * | |
| 1 бар | 1 | 10,2 | 1,020 | 0,9869 | 750 | 14,5 | |
| 1 м h3O | 9806,7 | 0,09807 | 1 | 0,1 | 0,09678 | 73,55 | 1,422 |
| 1 ат | 98,066 | 0,9807 | 10 | 1 | 0,9678 | 735,5 | 14,22 |
| 1 атм | 101,325 | 1,013 | 10,33 | 1,033 | 1 | 760 | 14,7 |
| 1 мм ртутного столба | 133,32 | 1,333 * | 0,0136 | 1,360 * | 1,316 * | 1 | 1,934* |
| 1 фунт/ | 6895 | 0,06895 | 0,7031 | 0,07031 | 0,06804 | 51,71 | 1 |
Таблица 2 – Коэффициенты для перевода
|
Наименование показателя |
Обозначение единицы СИ |
Наименование |
Переводной коэффициент |
|
Объемный расход жидкости |
м3/с |
Литр в секунду |
10-3 |
|
Кубический метр в час |
1/3600 |
||
|
Литр в час |
1/3600000 |
||
|
Литр в минуту |
1/60000 |
||
|
Галлон (ан.) в минуту |
75,77·10-6 |
||
|
Кубический фунт в секунду |
28,3168·10-3 |
||
|
Галлон (ам.) в минуту |
63,09·10-6 |
||
|
Баррель (ам.) в час (для нефти) |
44,16·10-6 |
||
|
Массовый расход жидкости |
кг/с |
Тонна в секунду |
103 |
|
Тонна в час |
1/3,6 |
||
|
Килограмм в час |
1/3600 |
||
|
Фунт в секунду |
0,45359237 |
||
|
Давление |
Па |
Килопонд на квадратный сантиметр |
98066,5 |
|
Килограмм-сила на квадратный сантиметр |
98066,5 |
||
|
Бар |
105 |
||
|
Гектопьез |
105 |
||
|
Давление |
Па |
Торр |
133,322 |
|
Общепринятый миллиметр ртутного столба |
133,322 |
||
|
Общепринятый миллиметр водяного столба |
9,80665 |
||
|
Паундаль на квадратный фут |
1,48816 |
||
|
Плотность |
кг/м3 |
Стандартная атмосфера |
101325 |
|
Фунт-сила на квадратный дюйм |
6894,76 |
||
|
Килограмм на кубический дециметр |
103 |
||
|
Грамм на кубический сантиметр |
103 |
||
|
Фунт на кубический фут |
16,0185 |
||
|
Мощность |
Вт |
Киловатт |
103 |
|
Килопонд·метр в секунду |
9,80665 |
||
|
Международная тепловая килокалория в час |
1,163 |
||
|
Лошадиная сила |
745,7 |
||
|
Британская тепловая единица в час |
0,293071 |
||
|
Килограмм-сила·метр в секунду |
9,80665 |
||
|
Вязкость (динамическая вязкость) |
Пас (кг/м с) |
Пуаз |
10-1 |
|
Дина-секунда на квадратный сантиметр |
10-1 |
||
|
Грамм на секунду-сантиметр |
10-1 |
||
|
Килопонд·секунда на квадратный метр |
9,80665 |
||
|
Сантипуаз |
10-3 |
||
|
Паундальсекунда на квадратный фут |
1,48816 |
||
|
Кинематическая вязкость |
м2/с |
Стокc |
10-4 |
|
Квадратный фут в секунду |
92,903·10-3 |
||
|
мм2/с |
Сантистокc |
1 |
uodn.ru
изучение зависимости коэффициента вязкости от температуры
Знания, полученные в этой работе, потребуются при рассмотрении вопросов гемодинамики на кафедрах физиологии, пропедевтики внутренних болезней, а также при изучении свойств биологических и лекарственных жидкостей на кафедрах внутренних болезней, фармакологии и др.
ЦЕЛЬ: Определить температурную зависимость вязкости жидкости и энергию активации ее молекул.
Для реализации цели необходимо:
а) Изучить литературу [1] по теме работы, раздел «Течение и свойства жидкостей».
б) Ответить на вопросы.
1. Что является причиной внутреннего трения жидкости с точки зрения молекулярной теории?
2. Как формируется закон Ньютона для течения реальной жидкости?
3. Что называется вязкостью жидкости?
4. Что такое ньютоновская и неньтоновская жидкости?
5. В каких единицах измеряется вязкость?
7. Какие методы измерения вязкости используются в медицине?
8. Что характеризуют динамическая и кинематическая вязкости?
9. Напишите и поясните выражение для силы Стокса и силы Архимеда.
10. Какие силы действуют на шарик, падающий в вязкой жидкости? Как эти силы связаны между собой в случае установившегося движения?
11. Что называется ламинарным и турбулентным течением? Что определяет число Рейнольдца?
12. Как зависит коэффициент внутреннего трения газов и жидкостей от температуры? Объясните эту зависимость на основе молекулярно-кинетической теории строения вещества.
13. В чем различие механизма возникновения внутреннего трения в газах и жидкостях?
14. Что называется энергией активации жидкости?
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ИССЛЕДОВАНИЯ
А). Вязкость жидкостей и газов
Возникновение
внутреннего трения в газах или жидкостях
обусловлено несколькими различными
причинами. В газах, где среднее расстояние
между молекулами в тысячи раз превышает
размеры молекул, силы взаимодействия
между молекулами настолько малы, что
движение молекул от столкновения до
столкновения происходит по прямой.
Возникновение силы внутреннего трения
в газах обусловлено только взаимным
проникновением молекул из одного слоя
в другой. Молекулы, проникшие из более
быстрого слоя 2 в слой 1, передают некоторый
импульс молекулам этого слоя. Это
равносильно действию на слой 1 некоторой
силы в направлении его движения. В свою
очередь молекулы, проникшие из более
медленного слоя 1 в слой 2, получают
некоторый импульс, что приводит к
торможению слоя 2, а это равносильно
действию силы F в направлении, противоположном движению.
Поскольку количество молекул, проникающих
из слоя 1 в слой 2 и наоборот, в среднем
одинаково, а переносимый ими импульс
разный (скорости слоев разные), в явлении
внутреннего трения в газах происходит
направленный перенос импульса молекул
в направлении от более быстрого слоя к
более медленному (от слоя 2 к слою 1).
Поэтому явление внутреннего трения
наряду с диффузией и теплопроводностью
относится к явлениям переноса. Следует
помнить, что коэффициент вязкости дня
газов возрастает с повышением температуры
(η ~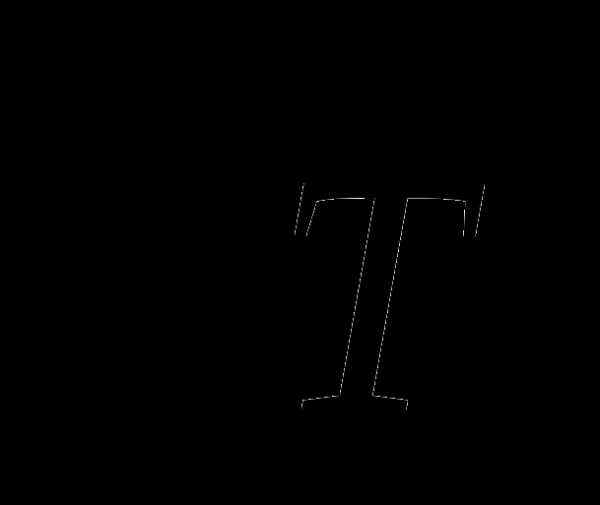 ).
Это объясняется тем, что с повышением
температуры газа увеличивается скорость
теплового движения молекул, что
способствует более интенсивному обмену
молекул между слоями и приводит к
увеличению направленного переноса
импульса молекул, т.е. к увеличению
вязкости.
).
Это объясняется тем, что с повышением
температуры газа увеличивается скорость
теплового движения молекул, что
способствует более интенсивному обмену
молекул между слоями и приводит к
увеличению направленного переноса
импульса молекул, т.е. к увеличению
вязкости.
В жидкостях, плотности которых в тысячи раз превышают плотность газа, среднее расстояние между молекулами сравнимо с их размерами. Поэтому силами взаимодействия между молекулами в жидкостях пренебрегать нельзя, и они сказываются при взаимном перемещении одних молекул относительно других. Кроме того, молекулы жидкости (в отличие от молекул газа) совершают колебательное движение относительно временных положений равновесия, меняя их через некоторые промежутки времени. Чем ниже температура жидкости, тем реже молекулы изменяют свои положения равновесия, и смещение одних молекул относительно других затруднено. Поэтому и вязкость жидкости при понижении температуры возрастает. Таким образом, вязкость в жидкостях обусловлена взаимодействием молекул и особым характером их теплового движения.
Механизмы переноса (диффузия, теплопроводность, вязкость) в жидкостях и газах существенно отличаются вследствие различия в их структуре. Молекулы в жидкости расположены близко друг к другу, поэтому свойства жидкостей в большей степени определяются характером межмолекулярных сил. Каждая молекула жидкости окружена со всех сторон «соседями», отстоящими от нее в среднем на расстоянии, близком к r0. Тепловое движение молекул сводится в основном к колебаниям внутри потенциальной ямы, созданной ее ближайшим окружением (место временной локализации) и перескоками ее из одного места локализации в другое. Так, за 1 с молекула жидкости меняет свое положение приблизительно 108 раз, совершая между двумя перескоками 103-105 колебаний.
Минимальная энергия, необходимая молекуле для преодоления потенциального барьера сил взаимодействия с ближайшим окружением и перескока в новое положение равновесия, называется энергией активации данной жидкости ɛ.
На полное освобождение отдельной молекулы от действия всех остальных необходимо затратить теплоту испарения. На разрушение порядка расположения молекул необходимо затратить теплоту плавления. Величина энергии активации лежит между теплотой испарения и теплотой плавления.
Уравнение переноса для жидкостей формально сохраняет тот же вид, что и для газов. Однако вследствие различного механизма переноса количества движения выражения для коэффициента газа и жидкости различны. Сущность явления внутреннего трения жидкости состоит в том, что молекулы, находящиеся под действием внешней силы, совершают перескоки преимущественно в направлении этой силы. Чем чаще способны молекулы жидкости перемещаться из одного мгновенного положения равновесия в другое, тем больше текучесть и меньше вязкость жидкости. Под текучестью жидкости понимают величину, обратную вязкости.
В отличие от газов с ростом температуры вязкость жидкости уменьшается. При критической температуре значение коэффициента вязкости пара и жидкости выравниваются.
Зависимость коэффициента вязкости от температуры для жидкостей описывается следующим уравнением:
, (1)
Где — коэффициент вязкости, W – энергия активации, T – абсолютная температура, k – постоянная Больцмана, A – коэффициент, который зависит от температуры.
При небольших интервалах температур Множитель А можно считать постоянным.
Из формулы (1) с учетом А=const получим:
.
Это уравнение представляет собой уравнение прямой линии
.
Тангенс угла наклона прямой представляет собой коэффициент . Зная постоянную Больцмана, можно вычислить энергию активации данной жидкости.
Б) Определение вязкости жидкости по методу Стокса
На движущийся шарик в жидкости действуют три силы: сила тяжести FТ, выталкивающая архимедова сила FА и сила сопротивления FC (рис. 3). Силу тяжести и выталкивающую силу можно определить следующим образом:
где r — радиус шарика; — плотность шарика; 0 — плотность жидкости.
Сила тяжести и выталкивающая сила постоянны. Сила сопротивления FC прямо пропорциональна скорости и поэтому на начальном этапе она меньше силы тяжести, и шарик падает равноускорено. При этом сила сопротивления увеличивается и наступает момент, когда все три силы уравновешиваются. Шарик начинает двигаться равномерно:
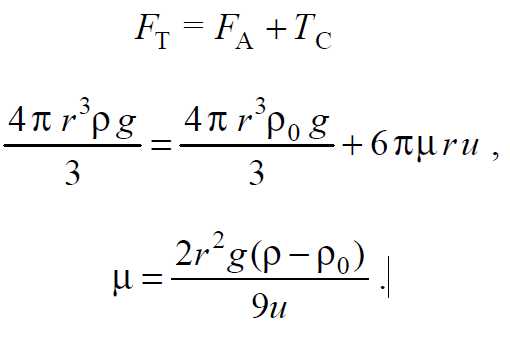 (1)
(1)
Для
определения вязкости жидкости по методу
Стокса берётся высокий цилиндрический
сосуд с исследуемой жидкостью (рис. 3).
На сосуде имеются две кольцевые метки А и В,
расположенные на расстоянии l друг
от друга. Уровень жидкости должен быть
выше верхней метки на l0 = 4…5 см, чтобы к моменту прохождения
шарика мимо верхней метки его скорость
можно было считать установившейся. 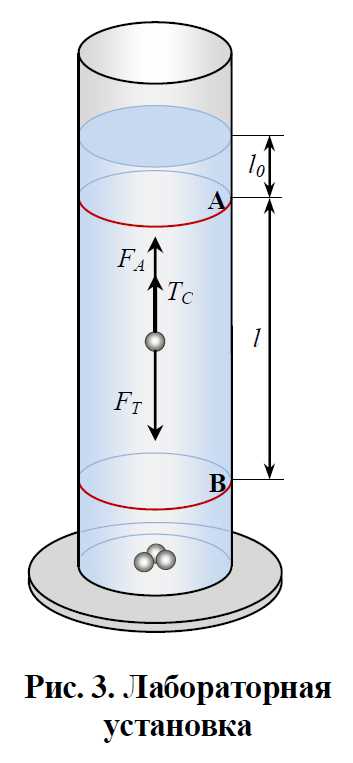
Бросая шарик в сосуд, отмечают по секундомеру время t прохождения шариком расстояния l=АВ между двумя метками.
Преобразуем формулу (1) путём подстановки выражения для скорости движения u = l/t и замены радиуса шарика r диаметром d:
(2),
где: — плотность шарика, 0 – плотность жидкости, — динамическая вязкость, g – ускорение свободного падения, d – диаметр шарика, t – время движения шарика от метки А до метки В, l – расстояние между метками.
Уравнение (2) справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки диаметром D, то приходится учитывать влияние боковых стенок.
При падении шарика диаметром d в цилиндрической трубе диаметром D, высотой h учёт влияния границ даёт:
(3)
Таким образом, зная плотности материала шарика и жидкости, радиусы шарика и сосуда, скорость установившегося движения шарика u, по формуле (3) можно вычислить динамическую вязкость жидкости.
ЗАДАНИЕ, ВЫПОЛНЯЕМОЕ В ЛАБОРАТОРИИ
Изменяя температуру воды, измерить время падения шарика в трубке. Рассчитать вязкость воды при различных температурах. Построить графики зависимостей . По второму графику рассчитать энергию активации воды.
ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ИССЛЕДОВАНИЯ
Лабораторная работа выполняется на установке фирмы PHYWE (рис. 1)
Лабораторная установка представляет собой вискозиметр с падающим шариком, который соединен с нагревательным элементом. Нагревательный элемент опущен в ванну с водой. На нагревательном элементе можно установить нужную температуру. С помощью насоса нагретая вода попадает в вискозиметр. С помощью секундомера устанавливается время падения шарика в жидкости.

Рис. 1 Общий вид экспериментальной установки.
МЕТОДИКА ПРОВЕДЕНИЯ ИССЛЕДОВАНИЯ
1) Налейте в ванну холодной воды так, чтобы вода не доходила до края на 5 см.
2) Включите установку в сеть. Включите нагревательный элемент.
3) После того, как вода заполнит вискозиметр, установите на нагревательном элементе температуру 10оС (значение температуры смотрите на электронном термометре).
4) Измерьте штангенциркулем диаметр стеклянного шарика. Вычислите плотность материала шарика по формуле: , где — объем шарика, m = 4 г – масса шарика.
5) Когда нужная температура установится, откройте вискозиметр и опустите туда стеклянный шарик.
6)Измерьте штангенциркулем внутренний диаметр трубки вискозиметра. Закройте вискозиметр (если с шариком в вискозиметр попал пузырек воздуха, его нужно выгнать с помощью стеклянной палочки!).
5) Переверните вискозиметр и засеките время прохождение им крайних меток.
6) Повторите измерения 5 раз, каждый раз переворачивая вискозиметр. Вычислите среднее значение времени. Измерения занесите в таблицу.
7) Повторите пункты 4-6, повышая температуру воды до 50оС с шагом в 5оС.
8) Измерьте расстояние пройденное шариком в вискозиметре.
9) Для каждой температуры рассчитайте вязкость жидкости по формуле (2) (плотность воды = 1000 кг/м3). Результаты занесите в таблицу.
10) Постройте графики зависимостей .
11) По второму графику рассчитайте коэффициент как тангенс угла наклона прямой с осью ОХ. Рассчитайте энергию активации данной жидкости.
12) Сделайте вывод о характере зависимости вязкости жидкости от температуры.
Таблица
ТС | Т, К | 1/Т | t, с | tср, с | , Пас | Ln() |
10 | ||||||
15 | ||||||
20 | ||||||
25 | ||||||
30 | ||||||
35 | ||||||
40 | ||||||
45 | ||||||
50 |
Отчет о проделанной работе сдайте преподавателю.
studfiles.net
223_вязкость_от_температуры
Лабораторная работа
»Исследование зависимости вязкости жидкости от температуры и концентрации на шариковом вискозиметре»
P1.8.3.3 Шариковый вискозиметр: измерение зависимости вязкости ньютоновской жидкости от температуры
Цель работы: определение вязкости жидкости и энергии активации.
Оборудование:
Вискозиметр Хепплера
Секундомер I
Циркуляционный термостат 20÷+100 °С
Набор для циркуляционного насоса
Силиконовая подводка, 7 мм Ø
Краткая теория.
Рассмотрим протекание жидкости по трубе. В том случае, когда соседние слои жидкости (или газа) перемещаются с различной скоростью, между ними действуют силы трения. Вязкостью называется свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Слой жидкости, непосредственно прилегающий к неподвижной плоскости, неподвижен. Линия тока жидкости в центре трубы перемещается с максимально скоростью. В промежуточной области скорость течения жидкости зависит от расстояния.
Основной закон вязкого течения был установлен И. Ньютоном
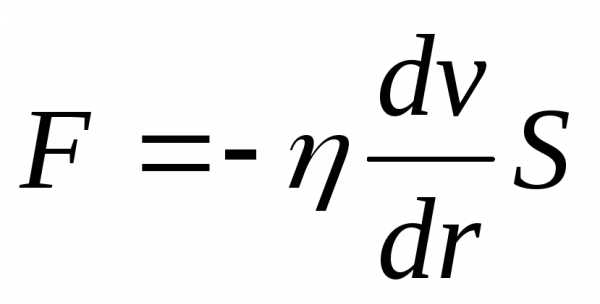 (1)
(1)
где сила трения F пропорциональна площади S плоскостей, перемещающихся относительно друг друга, и градиенту скорости dv/dr. Градиент dv/dr характеризует быстроту изменения скорости от слоя к слою. Коэффициент пропорциональности называется коэффициентом динамической вязкости. Он характеризует сопротивление жидкости (газа) смещению ее слоев. В системе СИ за единицу вязкости принят Паскальсекунда, сокращенно – Пас. Жидкость имеет вязкость один Пас, если для сдвига плоскости площадью 1 м2 параллельно другой плоскости, расположенной на расстоянии 1 м от первой, со скоростью 1 м/с требуется сила 1 Н. Если коэффициент динамической вязкости отнести к плотности жидкости, то получившеюся величину называют коэффициентом кинематической вязкости
=/; [ ] = []/[] = Пас/(кг/м3) = м2/с.
Когда жидкость (газ) перемещается как бы слоями, упорядоченно, течение жидкости называют ламинарным. Ламинарное течение жидкости наблюдается, например, при достаточно медленном течении жидкости в трубе. С увеличением скорости движения ламинарное течение в некоторый момент переходит в турбулентное течение, возникают вихри, происходит интенсивное перемешивание слоев жидкости, сопротивление жидкости изменяется (рис. 1).
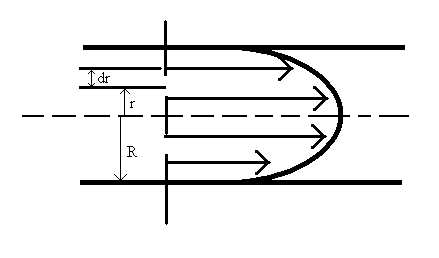
Рис. 1. Распределение скоростей движения жидкости в сечении трубы.
Характер течения определяется числом Рейнольдса
Re = v Lx/, (2)
где – плотность жидкости, – коэффициент динамической вязкости, v – скорость шарика, Lx – характерный размер тела. При рассмотрении течения жидкости в круглой трубе характерный размер имеет смысл радиуса трубы, а v имеет смысл средней скорости жидкости в сечении трубы. Если число Рейнольдса меньше критического значения Reкр, то возможно только ламинарное течение. Если Re больше критического значения, течение может иметь переходный или турбулентный характер. Критическое значение числа Рейнольдса зависит от состояния поверхности и других факторов. Для движения жидкости по трубе, как правило, Reкр= 2000 – 2200.
В системе СГС вязкость измеряется в дина-секунда на квадратный сантиметр (дин·сек/см2), равная 1 г/(см·сек) и названная пуазом (пз). Применяют дольные единицы пуаза — сантипуаз (спз), миллипуаз (мпз) и микропуаз (мкпз).
Нью́тоновская жи́дкость (названная так в честь Исаака Ньютона) — вязкая жидкость, подчиняющаяся в своём течении закону вязкого трения Ньютона
Примерами ньютоновской жидкости являются все низкомолекулярные вещества в жидком состоянии, их смеси и истинные растворы в них низкомолекулярных веществ (вода, органические жидкости, расплавленные металлы, соли и стекло при температуре выше температуры стеклования).
Экспериментальное изучение строения жидкостей показало, что в отличие от газов, жидкости обладают определенной структурой, называемой ближним порядком. Это означает, что число ближайших соседей отдельно выбранной молекулы, а также их взаимное расположение в среднем для всех молекул одинаковы. Подобно твердым телам жидкости мало сжимаемы, обладают большой плотностью; подобно газам – принимают форму сосуда, в котором находятся. Такой характер свойств жидкостей связан с особенностями теплового движения их молекул. По теории Я. Френкеля, молекулы жидкости, подобно частицам твердого тела, колеблются около положения равновесия, однако эти положения не являются постоянными. По истечении некоторого времени, называемого временем оседлой жизни, молекула скачком переходит в новое положение равновесия на расстояние, равное среднему расстоянию между соседними молекулами. Для того чтобы молекула жидкости «перескочила» из одного положения равновесия в другое, должны нарушиться связи с окружавшими ее молекулами и образоваться связи с новыми соседями. Для разрыва межмолекулярных связей требуется энергия Ea (энергия активации), выделяемая при образовании новых связей. Такой переход молекулы из одного положения равновесия в другое является переходом через потенциальный барьер высотой Еа. Энергию для преодоления потенциального барьера молекула получает за счет энергии теплового движения соседних молекул. Зависимость среднего времени свободной жизни молекулы () от температуры жидкости и энергии активации выражается формулой, вытекающей из распределения Больцмана:
| (3) |
где 0 – средний период колебаний молекулы около положения равновесия, k – постоянная Больцмана. Чем чаще молекулы меняют свои положения равновесия, тем более текуча и менее вязка жидкость, т.е. вязкость прямо пропорциональна . Учитывая формулу (3), получим выражения для температурной зависимости вязкости:
| (4) |
где
А — const.
Из графика температурной зависимости
вязкости можно определить энергию
активации. Для этого удобно прологарифмировать
уравнение (3)  и построить график в координатах ln и
1/T.
Тангенс угла наклона этого графика
будет равен энергии активации, поделенной
на постоянную Больцмана.
и построить график в координатах ln и
1/T.
Тангенс угла наклона этого графика
будет равен энергии активации, поделенной
на постоянную Больцмана.
Вязкость жидкостей и газов измеряют приборами, называемыми вискозиметрами. В представленной работе вязкость жидкостей и газов определяется сравнительным методом, в котором вязкость жидкости определяется по формуле:
(5),
где 1 плотность шарика, 2 плотность жидкости, К коэффициент, зависящей от размеров и плотности конкретного шарик, t время падения шарика в жидкости между двумя метками.

Ход работы:
Упражнение 1. Определение коэффициента К.
1. Измерьте массу и диаметр шарика.
2. Поместите шарик с неизвестным коэффициентом К в измерительную трубку.
3. Налейте жидкость с известной вязкостью в вискозиметр.
4. Переверните измерительную систему, измерьте время падения шарика в жидкости tмежду двумя крайними метками. Для более точного определения времени эксперимент следует проводить 4-6 раз.
5. Рассчитайте динамическую вязкость жидкости по формуле:
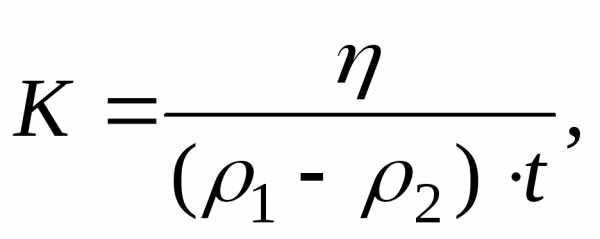
где 1 – плотность шарика;
2 – плотность жидкости;
— динамическая вязкость известной жидкости, приведённая в таблице.
Упражнение 2. Измерение вязкости ньтоновской жидкости.
Поместите шарик с измеренным коэффициентом в измерительную трубку.
Налейте жидкость, вязкость которой надо определить в вискозиметр.
Переверните измерительную систему, измерьте время падения шарика в жидкости tмежду двумя крайними метками. Для более точного определения времени эксперимент следует проводить 4-6 раз.
Рассчитайте динамическую вязкость жидкости по формуле:
где 1 – плотность шарика;
2 – плотность жидкости;
K — индивидуальная константа шарика
Включите нагреватель. Дождитесь повышение температуры на 1 градус.
Переверните измерительную систему, измерьте время падения шарика в жидкости tмежду двумя крайними метками. Для более точного определения времени эксперимент следует проводить 4-6 раз.
Проведите измерения при различных температурах. (5-6 значений). После каждого увеличения температуры ждите несколько минут, пока полностью прогреется исследуемая жидкость.
Постройте график зависимости коэффициента внутреннего трения жидкости от абсолютной температуры в координатах и Т.
Постройте график зависимости коэффициента внутреннего трения жидкости от абсолютной температуры в координатах
 и 1/T.
По тангенсу угла его наклона определите
энергию активации внутреннего трения
Еа.
и 1/T.
По тангенсу угла его наклона определите
энергию активации внутреннего трения
Еа.
Контрольные вопросы:
Явления переноса ( диффузия, теплопроводность, вязкость)
Какие течения жидкости называют ламинарными и турбулентными? Число Рейнольдса
Каков физический смысл коэффициента вязкости жидкости (газов)?
Закон Пуазейля.
Движение шарика в жидкости.
studfiles.net
Изучение зависимости коэффициента вязкости жидкости от температуры
Лабораторная работа 21
Изучение зависимости коэффициента вязкости жидкости от температуры.
Механизмы вязкости в газах и жидкостях существенно отличаются. В жидкостях расстояние между молекулами значительно меньше, чем в газах. Поэтому на движение молекул в жидкостях, в первую очередь, влияет межмолекулярное взаимодействие, ограничивая их подвижность. Вязкость жидкостей значительно больше, чем у газов и уменьшается с ростом температуры (у газов наоборот).
Молекулы жидкости могут совершать малые колебания лишь в пределах, ограниченных межмолекулярными расстояниями. Однако время от времени колеблющаяся молекула в результате флуктуации может получить от соседних молекул избыточную энергию, достаточную для того, чтобы совершить скачок на некоторое расстояние. В новом месте частица проведет некоторое время t, совершая колебания, пока снова не получит в результате флуктуации, нужную для скачка энергию; она вновь совершит скачок, и т. д. Такие колебания, сменяющиеся скачками – это и есть тепловые движения молекул жидкости. По образному выражению Френкеля Я.И., молекулы в жидкости ведут кочевой образ жизни, при котором кратковременные переезды сменяются относительно длительными периодами «оседлой» жизни. Среднее время t «оседлой» жизни молекул называется временем релаксации. Оно зависит от температуры. С повышением температуры t очень быстро уменьшается, что обуславливает увеличение подвижности молекул жидкости и, соответственно, уменьшение вязкости.
Для того, чтобы молекула жидкости перескочила из одного положения равновесия в другое, она должна нарушить связи с соседними молекулами. Для этого требуется затратить некоторую энергию W, т.е. молекула должна преодолеть потенциальный барьер высотой W. Величина W называется энергией активации.
Длительность пребывания молекулы в данном месте жидкости определяется вероятностью для молекулы получить энергию W, достаточную для скачка. А эта вероятность выражается законом Больцмана
Здесь n-число молекул в единице объёма, энергия которых равна W, n0 – число молекул в единице объёма с энергией W= 0.
Чем больше вероятность получения молекулой энергии W, тем меньше будет время «оседлости» t, т.е. . Поэтому для среднего времени релаксации можно написать выражение
.
Множитель А имеет смысл периода колебания молекулы.
Очевидно, что жидкость будет тем более текучей (с тем меньшей вязкостью), чем меньше время t«оседлости» молекул и , значит, чем чаще происходит скачок.
Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде
(1)
Множитель С, входящий в это выражение, зависит от рода жидкости, частоты колебаний молекул и температуры (~Т). При обычных температурах (kТ<W) из формулы (1) следует, что вязкость жидкости уменьшается с повышением температуры (в противоположность газам). Однако при достаточно больших температурах, когда kТ>W, вязкость начинает возрастать с температурой (как у газов).
Прологарифмируем формулу (1)
(2)
График зависимости от представляет собой прямую (рис.1). Из наклона этой прямой можно определить энергию активации W.
 (3)
(3)
k – постоянная Больцмана.
Это энергия активации для одной молекулы.
Энергия активации в расчёте на один моль жидкости
WМ = W·NА, NА— число Авогадро.
По справочным данным для водыWМ »16 Дж/моль.
В данной работе экспериментально определяется коэффициент вязкости воды при различных температурах и на основе этих измерений определяется энергия активации.
Экспериментально коэффициент вязкости измеряется вискозиметром с падающим шариком (метод Стокса).
На шарик действуют три силы: сила тяжести Р, направленная вниз; сила внутреннего трения и выталкивающая сила Fв, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, т.е.
vunivere.ru
1. Использовать методическое руководство к работе «Определение вязкости жидкости. Исследование зависимости вязкости от концентрации, температуры или градиента скорости»
2. Теплообмен с окружающей средой не скажется на навыках.
7. Ход занятия
Измерить ареометром плотности жидкостей: дистиллированной воды и растворов различной концентрации сахарозы. Для этого налить в мерный цилиндр исследуемую жидкость и осторожно опустить в него ареометр с самыми низкими значениями пределами измерения. Если уровень жидкости не доходит до шкалы этого ареометра, необходимо заменить его на ареометр, предназначенный для измерения плотности более плотных жидкостей. Плотность жидкости находят по делению шкалы ареометра, которое соответствует уровню жидкости. После измерения плотности одного из жидкостей необходимо промыть мерный цилиндр дистиллированной водой. Для уменьшения погрешности измерения рекомендуется начинать опыт с дистиллированной водой, затем с раствора с наиболее низкой концентрацией сахарозы и далее использовать растворы с возрастающей концентрацией.
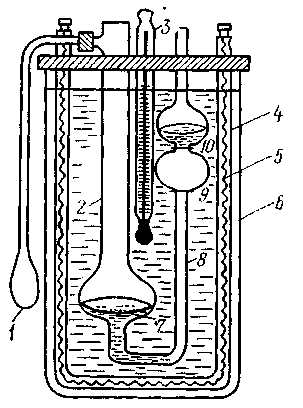
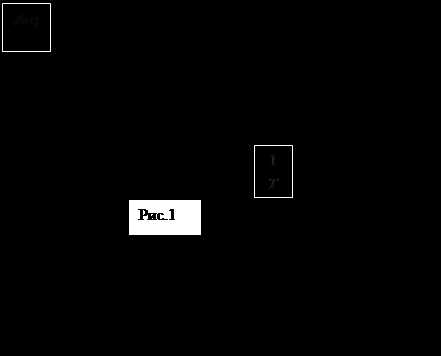
В вискозиметр наливают исследуемый раствор заполняя расширение 7 и погружают его в сосуд 6 . Сосуд 6 выполняет роль термостата. Закрыв пальцем руки отверстие колена 2, грушей 1 медленно нагнетают измеряемую жидкость в правое колено через капилляр 8 в расширение, находящееся выше метки 10 . Отнимают палец и освобождают грушу, после чего исследуемая жидкость начинает медленно вытекать через расширение, так как она расположена выше чем жидкость в расширении 7 сообщающих сосудов. В момент прохождения мениска жидкости через метку 10 включают секундомер , останавливают его в момент прохождения мениска через метку 9.

Измерить по 3 раза время вытекания растворов различной концентрации исследуемого раствора из вискозиметра Оствальда. Для уменьшения погрешности измерения рекомендуется начинать опыт с раствора с наиболее низкой концентрацией, затем использовать растворы с возрастающей концентрацией.
Аналогичным образом произвести измерение времени истечения жидкости сравнения после трех кратного промывания вискозиметра стандартным раствором .
Данные измерений занести в таблицу.
Таблица 1
С, % | ρ. 10-3, кг/м3 | t, сек | ||||
ρ1 | ρ2 | ρ3 | t1 | t2 | t3 | |
Стандартная жидкость | ||||||
5 | ||||||
20 | ||||||
40 | ||||||
х | ||||||
По результатам измерений относительным методом, второе название «метод сравнения», третье название « метод нахождения постоянной прибора» найдем вязкость исследуемой жидкости по известной вязкости стандартной жидкости. В качестве стандартной жидкости будем использовать воду. Данные для разных температур вязкости и плотности воды возьмем из таблицы.
Плотность и вязкость воды при различных температурах.
t, 0C | , кг/м3 | ·103, Па · с |
0 | 999,87 | 1,79 |
5 | 999,99 | 1,52 |
10 | 999,73 | |
15 | 999,13 | 1,14 |
20 | 998,23 | 1,00 |
25 | 997,07 | 0,89 |
30 | 995, 67 | 0,80 |
35 | 994,06 | 0,72 |
Объем истекающей жидкости между метками 9 и 10 одинаков, из формулы Пуазейля, как для воды так и для исследуемой жидкости т.е.
где Δp , t, η – разность давления между метками 9 и 10, время истечения, вязкость исследуемого раствора, а Δp0 , t0, η0— соответствующие величины для стандартной жидкости. При этом Δp и Δp0 можно выразить через произведение g- ускорение свободного падения на плотность жидкости ρ ( ρ-исследуемой или ρ0— стандартной), на среднюю высоту между метками 9 и 10 Δhср. Если нам известны значения плотности и вязкости стандартной жидкости для выбранной температуры опыта при использовании одного вискозиметра Оствальда или вискозиметров типа ВПЖ для определения времени истечения как стандартной так и исследуемой жидкости, вязкость можно найти по формуле
η0=kgρ0 t0
где k- постоянная прибора и определяется через параметры вискозиметра и не зависит от используемых жидкостей для измерения, равна
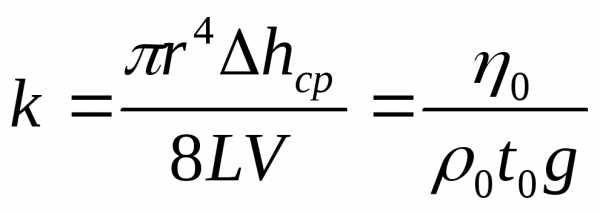
k-зависит от температуры и ускорения свободного падения и времени протекания жидкости между метками 9 и10. Искомая вязкость раствора будет равна
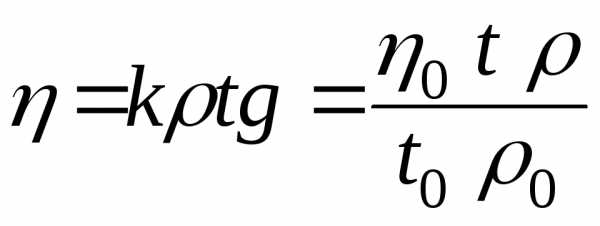
По конечной формуле видно, что мы сравнили величины характеризующие исследуемую жидкость и стандартную , получили метод сравнения. С другой стороны искомая величина рассмотрена относительно стандартной величины, относительный метод.
При проведении трех измерений на каждый исследуемый раствор ,расчетная формула для вязкости раствора имеет вид:
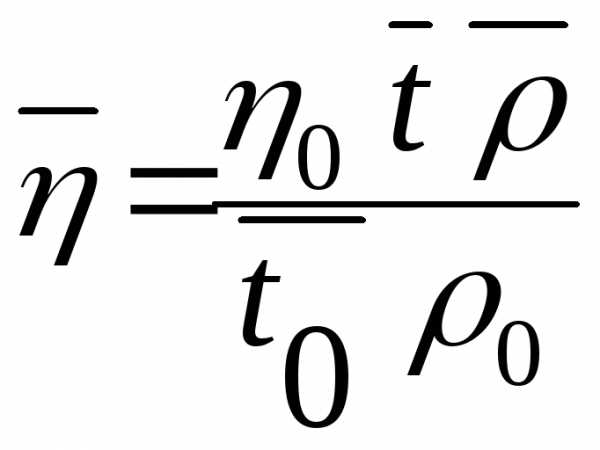 (1),
(1),
где 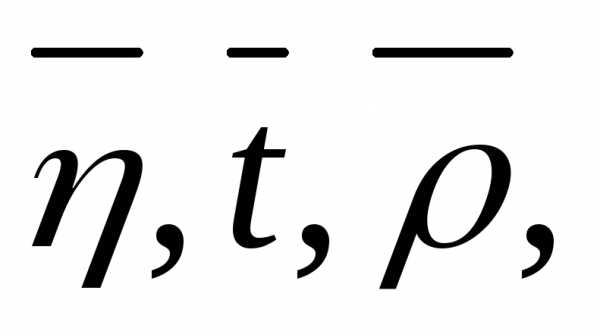 — среднее значение изn
измерений вязкости, времени истечения
из вискозиметра и плотность для
исследуемой жидкости и
— среднее значение изn
измерений вязкости, времени истечения
из вискозиметра и плотность для
исследуемой жидкости и 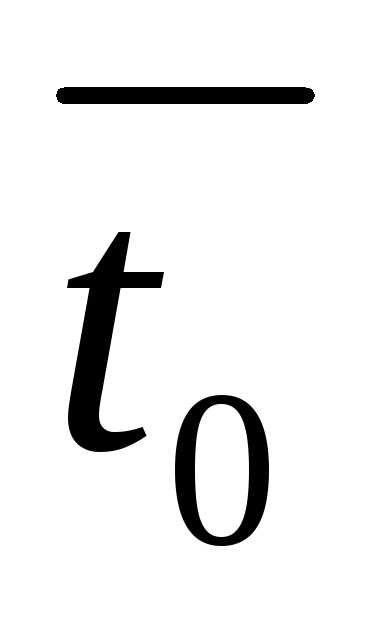 времени истечения воды из вискозиметра
,0 , 0 — вязкость, и плотность воды взятые из
таблицы.
времени истечения воды из вискозиметра
,0 , 0 — вязкость, и плотность воды взятые из
таблицы.
Конечный результат представляется в виде
 ,
,
где Δη- доверительный интервал где находится истинное значение определяемой вязкости. Δη определяется по формуле
где tα,n-коэффициент Стьюдента при доверительной вероятности α= 0,95 (или 0,99 или 0,999), и числе измерений n, или n-1 степеней свободы. Данный коэффициент берется из таблицы. Определим по формулам:
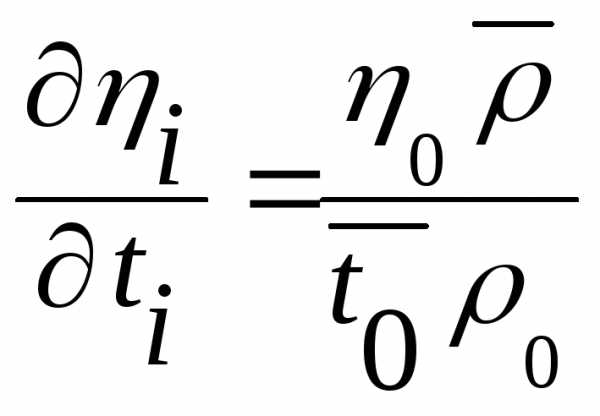 ;
; 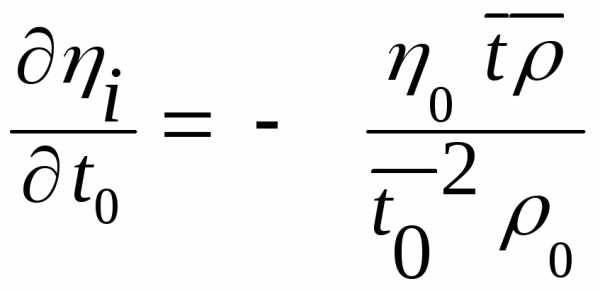 ;
;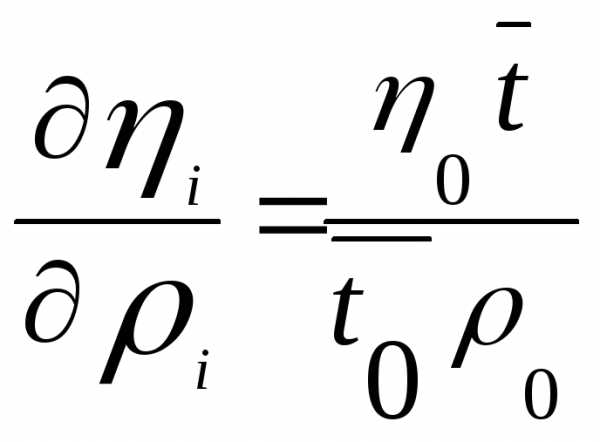 ,
а также
,
а также
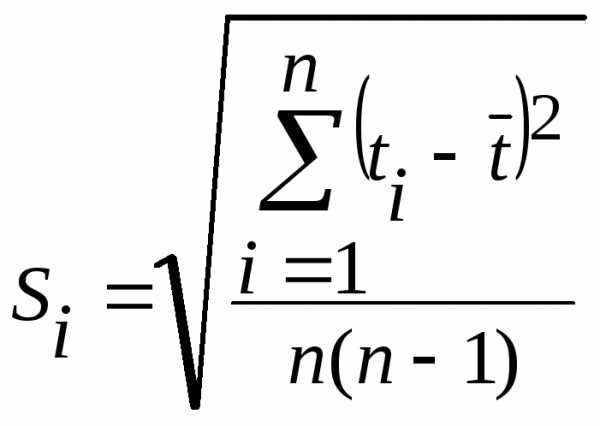 ;
; 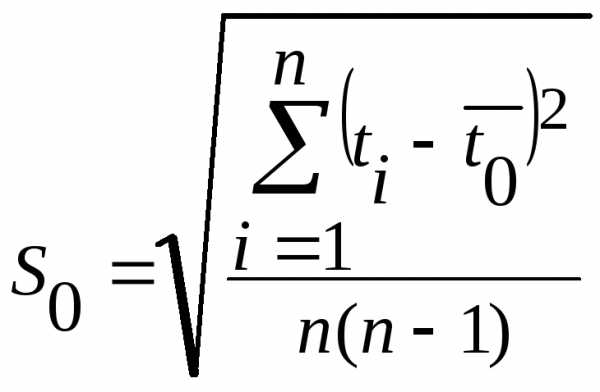 ;
;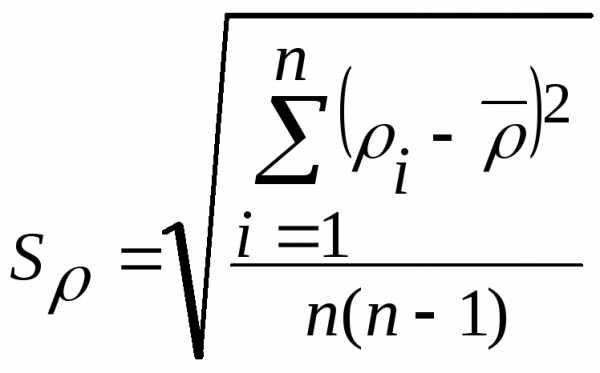 ,
а также
,
а также
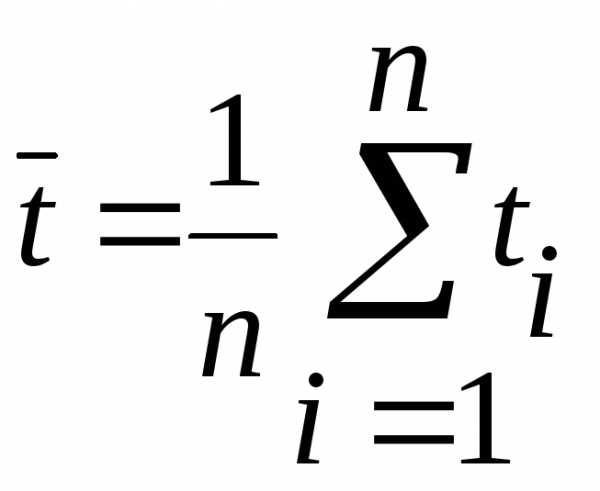 ;
; 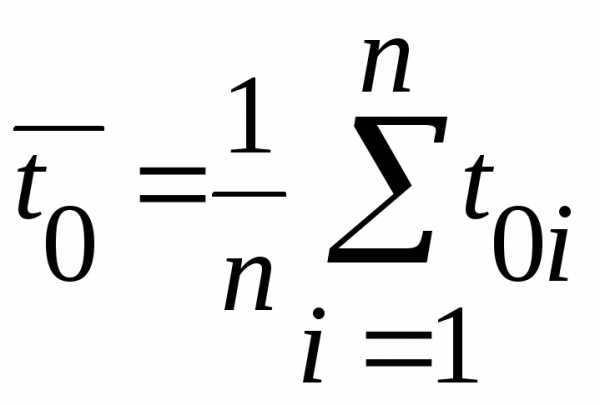 ;
;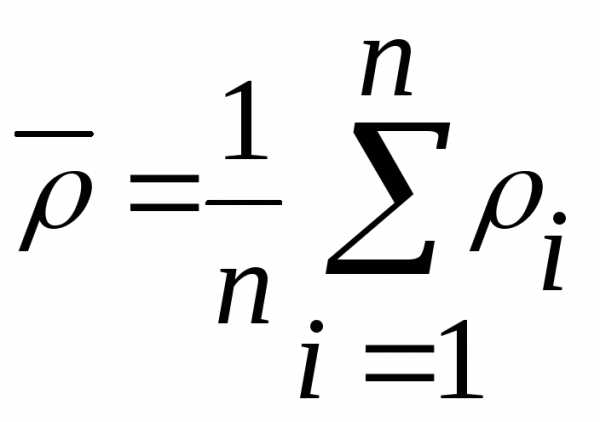
Рассчитать по формулам величины и занести результаты вычислений в таблицу.
Таблица 2
С, % | (среднее значение), | Среднеквадратическая, среднеарифметического | . 103 (среднее значение), Па.сек | . 103, Па.сек | ||||
| | | Si | S0 | Sρ | |||
0 | 1,00 | — | ||||||
5 | — | |||||||
20 | — | |||||||
40 | — | |||||||
x | ||||||||
Построить график зависимости коэффициента вязкости раствора от концентрации сахарозы в растворе η=f(С). По графику определить неизвестную концентрацию раствора сахарозы, зная величину коэффициента вязкости этого раствора.
Сделать вывод по результатам работы. В выводе указать искомую концентрацию раствора х (%) и коэффициент вязкости этого раствора (Па . сек) и как изменяется коэффициент вязкости с увеличением концентрации сахарозы в растворе.
8. ЛИТЕРАТУРА
1.Конспект лекций.
2.Ремизов А.Н. Медицинская и биологическая физика: Учеб. для мед. спец. вузов.– 2-е изд. испр.– М.: Высш. школа, 1996.–608 с.
3.Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике: Учебн. пособие.– 2-е изд., перераб. и доп. – М: Дрофа, 2001.– 192 с.
4.Блохина М.Е., Эссаулова И.А., Мансурова Г.В. Руководство к лабораторным работам по медицинской и биологической физике: Учебн. пособие. – 3-е изд., стереотип. – М.: Дрофа, 2002.– 288 с.
Министерство здравоохранения республики Беларусь
Учреждение образования
«Гомельский государственный медицинский университет»
Кафедра медицинской и биологической физики
studfiles.net

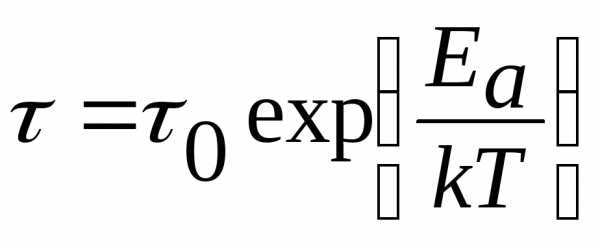 ,
,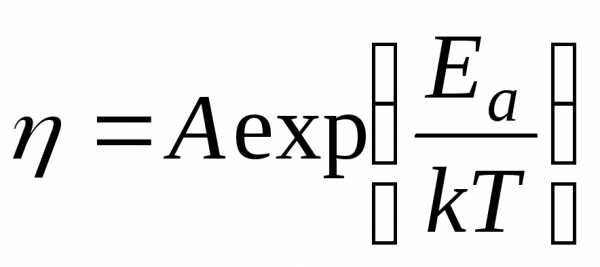 ,
,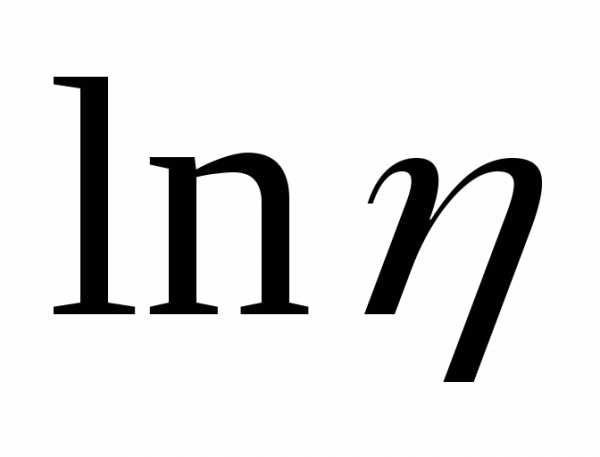 и 1/T.
По тангенсу угла его наклона определите
энергию активации внутреннего трения
Еа.
и 1/T.
По тангенсу угла его наклона определите
энергию активации внутреннего трения
Еа.