Зависимость вязкости от температуры —
С повышением температуры вязкость капельных жидкостей и их смесей понижается.
Математических уравнений, пригодных для практического применения, выражающих закон изменения вязкости от температуры, до настоящего времени не имеется, поэтому пользуются эмпирическими зависимостями. Для минеральных масел с вязкостью > 80 ccm при температурах от 30 до 1500 С пользуются выражением
где и – кинематические коэффициенты вязкости при заданной температуре t и температуре 500 С в ccm;
n – показатель степени, значения которого в зависимости от исходной вязкости при 500 С приведены ниже.
| Вязкость | 2,8 | 6,25 | 9,0 | 11,8 | 21,2 | 29,3 |
| Показатель n | 1,39 | 1,59 | 1,72 | 1,79 | 1,99 | 2,13 |
| Вязкость | 37,3 | 45,1 | 52,9 | 60,6 | 68,4 | 80,0 |
| Показатель n | 2,24 | 2,32 | 2,42 | 2,49 | 2,52 | 2,56 |
В гидросистемах применяются жидкости, вязкость которых при 500 С составляет 10-100 спз. В частности вязкость применяемого в самолетных гидросистемах масла АМГ – 10 при 500 С равна 10 ccm.
Зависимость вязкости распространенных масел от температуры показана на рис. 2. а и б. Очевидно, чем меньше изменяется вязкость с изменением температуры, тем выше качество и лучше эксплуатационные свойства рабочей жидкости. При применении жидкостей, имеющих крутую кривую температурной зависимости вязкости, затруднена работа гидросистемы в зимних условиях эксплуатации.
Обычно вязкостно – температурные свойства жидкостей характеризуются отношением Жидкость, предназначенная для эксплуатации в широком температурном интервале, считается пригодной, если ее вязкость при изменении температуры от – 500 С до + 500 С изменяется не более, чем в 100 раз.
Рис. 2. Графики зависимости динамической вязкости
масел от температуры:
1 – трансформаторное; 2 – индустриальное 12;
3- индустриальное 20; 4 – индустриальное 30;
5- индустриальное 50; 6- автотракторное;
7- МВП; 8- ЦИАТИМ-1; 9- АМГ-10
einsteins.ru
Исследование зависимости вязкости моторного масла от температуры
Томск — это город, в котором зима бывает очень суровой. И ежегодно среди автомобилистов возникает проблема сложного, а порой и невозможного, запуска двигателя автомобиля в зимних условиях. Эта проблема может возникнуть по ряду причин. Когда двигатель холодный, наоборот, масло обладает тенденцией сгущаться. И, как следствие, невозможность прокрутки вала двигателя. Моторное масло играет важнейшую роль в эксплуатации двигателя автомобиля. Его основная задача — это смазка. Моторное масло разных видов и сортов отличается по характеристикам, определяющим сферу их применения. В зависимости от характеристик, масло рекомендуется для использования в разных типах двигателей, работающих в различных условиях и температурных режимах. Для покупателей наибольшую важность представляют два показателя: вязкость (позволяет определить, подойдет ли масло для определенного сезона и климата) и допуск (подходит ли масло для данного автомобиля). Причем даже для одного и того же типа масла, но разных марок показатель вязкости может отличаться в зависимости от температурных условий. Исходя из этого, нами была поставлена следующая
Для реализации поставленной цели решались следующие задачи:
- Изучить классификацию моторных масел;
- Изучить характеристики моторных масел;
- Определить вязкость моторных масел при различных (низких) температурах;
- Сформулировать рекомендации автомобилистам по применению различных масел при низких температурах.
Объект исследования: моторное масло.
Предмет исследования: вязкость.
Методы исследования.
Теоретические: анализ информации по темам “Моторные масла”, “Характеристики моторных масел”, “Вязкость и способы ее измерения”.
Практические: эксперимент по определению вязкости (кинематической и динамической) моторных масел при различных температурах.
Моторное масло — это смазочный материал, который используется с целью уменьшения трения в движущихся частях двигателей внутреннего сгорания.
Первое в мире моторное масло было запатентовано в 1873 году американским доктором Джоном Эллисом. В 1866 году Эллис изучал свойства сырой нефти в медицинских целях, но обнаружил, что сырая нефть обладает хорошими смазочными свойствами. Джон Эллис зарегистрировал Valvoline — первый в мире бренд моторного масла.
Моторное масло разделяется на три типа: минеральное, синтетическое и полусинтетическое.
Существует классификация масел по вязкостно-температурным свойствам и классификация масел по эксплуатационным свойствам (назначению и качеству). В настоящее время единственной признанной во всем мире системой классификации транспортных масел по вязкости является спецификация SAE (Американская ассоциация автомобильных инженеров).
Норма SAE J 300 определяет степень вязкости для каждого смазочного материала.
SAE J-300 содержит 6 зимних классов и 5 летних классов моторных масел.
Классы вязкости SAE OW, 5W, 10W, 15W, 20W, 25W относятся к зимним, а SAE 20, 30, 40, 50, 60 — к летним.
Надежность работы двигателя во многом определяется выбором масла с оптимальной вязкостью.
Вязкость — это одна из важнейших характеристик масел, которая характеризует внутреннее трение, определяет текучесть и способность обеспечить жидкостной режим смазывания. Различают кинематическую и динамическую вязкость.
Кинематическая вязкость, характерная для простых масел при положительных температурах, определяется в капиллярных вискозиметрах, а динамическая — для загущенных (всесезонных) масел и масел при отрицательных температурах, определяется в ротационных вискозиметрах, ее величина зависит не только от температуры, но и от градиента скорости сдвига.
Динамическую вязкость представляет собой произведение кинематической вязкости на плотность жидкости, в технической системе ее измеряют в сантипуазах (сП), а в системе СИ — в миллиПаскаль-секундах (мПа-с), где 1 сП= 1 мПа-с. Это сопротивление, которое оказывает жидкость при относительном перемещении двух ее слоев поверхностью 1 м
Кинематическую вязкость в технической системе единиц измеряют в Стоксах (Ст) или сантистоксах (сСт), а в системе СИ в м2/с или в мм2/с. Кинематической вязкостью [ν] называется величина, равная отношению динамической вязкости жидкости [μ] к ее плотности [ρ] при той же температуре: ν = μ/ρ.
В ходе эксперимента была измерена динамическая (методом Стокса) и кинематическая (вискозиметром ВПЖ-2, d=1,77 мм) вязкость при различных температурах для следующих марок масла:
- ZIC XQ 5w40
- Helix HX7 5w40
- Castrol Magnatec 5w40
Кинематическая вязкость определялась по следующей формуле:
K — постоянная вискозиметра (1,022 )
T — время истечения жидкости, с
ν — кинематическая вязкость жидкости, мм2/с
g — ускорение свободного падения (м/с2)
Результаты измерений показаны в таблице 1.
Таблица 1. Кинематическая вязкость (вискозиметр)
|
Масло |
t = +210С |
t = -70С |
t = -140C |
t = -180C |
t = -210 |
|||||
|
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
Тср, с |
ν, мм2/с |
|
|
ZIC XQ 5w40 |
143 |
146,04 |
153 |
156,25 |
192 |
196,08 |
198 |
202,21 |
241 |
246,13 |
|
Helix HX7 5w40 |
139 |
141,957 |
188 |
191,99 |
199 |
203,23 |
224 |
228,76 |
246 |
251,24 |
|
Castrol Magnatec 5w40 |
128 |
130,723 |
176 |
179,74 |
230 |
234,89 |
236 |
241,02 |
239 |
244,08 |
Таким образом, можно сделать следующие выводы: 1) вязкость масла увеличивается с понижением температуры; 2) Из всех марок масел меньше всего увеличилась вязкость Castrol Magnatec.
Динамическая вязкость (Па*с) определялась по следующей формуле:
t – время падения, с
r – радиус шарика, м
R0– радиус сосуда, м
l – высота падения, м
ρ – плотность шарика, кг/м3
ρ0 – плотность жидкости, кг/м3
Для измерения вязкости использовалась следующая установка (рис. 1).
Значения динамической вязкости представлены в таблице 2.
ρ = 8900 кг/м3
l = 0,14 м
r = 2 мм
R0 = 0,015 м
Значения плотности масел:
Плотность масла ZIC XQ (при всех температурах): 1660 кг/м3.
Плотность масел Helix HX7 и Castrol Magnatec (при всех температурах): 1760 кг/м3.
Таблица 2. Динамическая вязкость (метод Стокса)
|
Масло |
t = +210С |
t = -70С |
t = -140C |
t = -180C |
t = -210C |
|||||
|
, cм/с |
μ, Па·с |
, cм/с |
μ, Па·с |
, cм/с |
μ, Па·с |
, см/с |
μ, Па·с |
, см/с |
μ, Па·с |
|
|
ZIC XQ 5w40 |
4,59 |
0,503 |
9,59 |
0,838 |
11,13 |
1,07 |
15,01 |
1,109 |
17,65 |
1,305 |
|
Helix HX7 5w40 |
1,73 |
0,34 |
4,83 |
0,81 |
7,53 |
0,996 |
10,35 |
1,505 |
13,12 |
2,103 |
|
Castrol Magnatec 5w40 |
2,56 |
0,34 |
6,36 |
0,76 |
9,48 |
0,859 |
12,15 |
1,370 |
15,95 |
2,59 |
Таким образом, можно сделать вывод, что при понижении температуры динамическая вязкость увеличивается. Причем у масла Castrol Magnatec интенсивнее, чем у ZIC и Helix.
Динамическая вязкость важна при определении низкотемпературных свойств смазок, но её редко применяют при анализе масла или для определения класса вязкости. По многим разным причинам, исследователя масла интересует кинематическая вязкость. А по этому показателю лучшие свойства показало масло Castrol Magnatec. Но сказать, что остальные масла более худшего качества нельзя. Их показатели вязкости незначительно отличаются от Castrol Magnatec и все значения укладываются в рамки допустимых производителем.
Следует отметить, что эффективность работы мотора зависит не от абсолютного значения вязкости при определенных температурах, а от динамики ее изменений при работе в определенных диапазонах рабочих температур, а также соответствие этой динамики конструкции данного двигателя. Если двигатель рассчитан на параметры авто-масла 5w30, тогда моторное масло с маркировкой 0w20 не подходит и его заливать нельзя, а с маркировкой 5w40 не рекомендуется. Значит, использовать то авто-масло, которое подходит согласно требованиям производителя двигателя, но ни в коем случае не рекомендациям изготовителя авто-масла.
В целом по маслам можно дать следующие рекомендации:
− перечень марок масел, допущенных к применению, постоянно изменяется, получают допуск новые марки, некоторые его теряют;
− температурный диапазон применения, указанный на упаковке масла, носит лишь рекомендательный характер;
− не стоит оценивать масла по цвету, большинство вводимых в него присадок делают его более темным;
− замену масла при тяжелых условиях эксплуатации необходимо производить в 1,5—2 раза чаще, тоже рекомендуется делать для автомобилей со значительным пробегом, так как условия его работы в изношенных двигателях более жесткие, в частности из-за окисляющего действия сгоревших газов, попадающих в масляный катер;
− быстрое (через 1—2 тыс. км пробега) почернение масла не обязательно указывает на потерю его эксплуатационных свойств;
− доливать следует тот же сорт масла, который залит в двигатель, так как масла разных производителей содержат различные пакеты присадок и смешивание может ухудшить их свойства;
− нежелательно смешивать минеральные и синтетические масла, а также доливать минеральное в полусинтетическое из-за разной растворимости присадок в минеральной и синтетической основах;
− если неизвестно, что использовал прежний владелец автомобиля, перед заменой желательно промыть систему смазки;
− добавление в моторное масло различных препаратов может улучшить одни его свойства и резко ухудшить другие.
e-koncept.ru
Изучение зависимости коэффициента вязкости жидкости от температуры
Лабораторная работа 21
Изучение зависимости коэффициента вязкости жидкости от температуры.
Механизмы вязкости в газах и жидкостях существенно отличаются. В жидкостях расстояние между молекулами значительно меньше, чем в газах. Поэтому на движение молекул в жидкостях, в первую очередь, влияет межмолекулярное взаимодействие, ограничивая их подвижность. Вязкость жидкостей значительно больше, чем у газов и уменьшается с ростом температуры (у газов наоборот).
Молекулы жидкости могут совершать малые колебания лишь в пределах, ограниченных межмолекулярными расстояниями. Однако время от времени колеблющаяся молекула в результате флуктуации может получить от соседних молекул избыточную энергию, достаточную для того, чтобы совершить скачок на некоторое расстояние. В новом месте частица проведет некоторое время t, совершая колебания, пока снова не получит в результате флуктуации, нужную для скачка энергию; она вновь совершит скачок, и т. д. Такие колебания, сменяющиеся скачками – это и есть тепловые движения молекул жидкости. По образному выражению Френкеля Я.И., молекулы в жидкости ведут кочевой образ жизни, при котором кратковременные переезды сменяются относительно длительными периодами «оседлой» жизни. Среднее время t «оседлой» жизни молекул называется временем релаксации. Оно зависит от температуры. С повышением температуры t очень быстро уменьшается, что обуславливает увеличение подвижности молекул жидкости и, соответственно, уменьшение вязкости.
Для того, чтобы молекула жидкости перескочила из одного положения равновесия в другое, она должна нарушить связи с соседними молекулами. Для этого требуется затратить некоторую энергию W, т.е. молекула должна преодолеть потенциальный барьер высотой W. Величина W называется энергией активации.
Длительность пребывания молекулы в данном месте жидкости определяется вероятностью для молекулы получить энергию W, достаточную для скачка. А эта вероятность выражается законом Больцмана
Здесь n-число молекул в единице объёма, энергия которых равна W, n0 – число молекул в единице объёма с энергией W= 0.
Чем больше вероятность получения молекулой энергии W, тем меньше будет время «оседлости» t, т.е. . Поэтому для среднего времени релаксации можно написать выражение
.
Множитель А имеет смысл периода колебания молекулы.
Очевидно, что жидкость будет тем более текучей (с тем меньшей вязкостью), чем меньше время t«оседлости» молекул и , значит, чем чаще происходит скачок.
Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде
(1)
Множитель С, входящий в это выражение, зависит от рода жидкости, частоты колебаний молекул и температуры (~Т). При обычных температурах (kТ<W) из формулы (1) следует, что вязкость жидкости уменьшается с повышением температуры (в противоположность газам). Однако при достаточно больших температурах, когда kТ>W, вязкость начинает возрастать с температурой (как у газов).
Прологарифмируем формулу (1)
(2)
График зависимости от представляет собой прямую (рис.1). Из наклона этой прямой можно определить энергию активации W.
 (3)
(3)
k – постоянная Больцмана.
Это энергия активации для одной молекулы.
Энергия активации в расчёте на один моль жидкости
WМ = W·NА, NА— число Авогадро.
По справочным данным для водыWМ »16 Дж/моль.
В данной работе экспериментально определяется коэффициент вязкости воды при различных температурах и на основе этих измерений определяется энергия активации.
Экспериментально коэффициент вязкости измеряется вискозиметром с падающим шариком (метод Стокса).
На шарик действуют три силы: сила тяжести Р, направленная вниз; сила внутреннего трения и выталкивающая сила Fв, направленные вверх. Шарик сначала падает ускоренно, но затем очень быстро наступает равновесие, т.е.
vunivere.ru
Плотность воздуха, его удельная теплоемкость, вязкость и другие физические свойства: таблицы при различных температурах
Рассмотрены основные физические свойства воздуха: плотность воздуха, его динамическая и кинематическая вязкость, удельная теплоемкость, теплопроводность, температуропроводность, число Прандтля и энтропия. Свойства воздуха даны в таблицах в зависимости от температуры при нормальном атмосферном давлении.
Плотность воздуха в зависимости от температуры
Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа. Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.
На практике, чтобы узнать какова плотность воздуха при различных температурах, удобно воспользоваться готовыми таблицами. Например, приведенной таблицей значений плотности атмосферного воздуха в зависимости от его температуры. Плотность воздуха в таблице выражена в килограммах на кубический метр и дана в интервале температуры от минус 50 до 1200 градусов Цельсия при нормальном атмосферном давлении (101325 Па).
| t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 |
|---|---|---|---|---|---|---|---|
| -50 | 1,584 | 20 | 1,205 | 150 | 0,835 | 600 | 0,404 |
| -45 | 1,549 | 30 | 1,165 | 160 | 0,815 | 650 | 0,383 |
| -40 | 1,515 | 40 | 1,128 | 170 | 0,797 | 700 | 0,362 |
| -35 | 1,484 | 50 | 1,093 | 180 | 0,779 | 750 | 0,346 |
| -30 | 1,453 | 60 | 1,06 | 190 | 0,763 | 800 | 0,329 |
| -25 | 1,424 | 70 | 1,029 | 200 | 0,746 | 850 | 0,315 |
| -20 | 1,395 | 80 | 1 | 250 | 0,674 | 900 | 0,301 |
| -15 | 1,369 | 90 | 0,972 | 300 | 0,615 | 950 | 0,289 |
| -10 | 1,342 | 100 | 0,946 | 350 | 0,566 | 1000 | 0,277 |
| -5 | 1,318 | 110 | 0,922 | 400 | 0,524 | 1050 | 0,267 |
| 0 | 1,293 | 120 | 0,898 | 450 | 0,49 | 1100 | 0,257 |
| 10 | 1,247 | 130 | 0,876 | 500 | 0,456 | 1150 | 0,248 |
| 15 | 1,226 | 140 | 0,854 | 550 | 0,43 | 1200 | 0,239 |
При 25°С воздух имеет плотность 1,185 кг/м3. При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м3, что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение плотности газов при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.
Если сравнить плотность воздуха относительно плотности воды, то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м3, а плотность воздуха составляет 1,27 кг/м3. Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м3.
Динамическая и кинематическая вязкость воздуха при различных температурах
При выполнении тепловых расчетов необходимо знать значение вязкости воздуха (коэффициента вязкости) при различной температуре. Эта величина требуется для вычисления числа Рейнольдса, Грасгофа, Релея, значения которых определяют режим течения этого газа. В таблице даны значения коэффициентов динамической μ и кинематической ν вязкости воздуха в диапазоне температуры от -50 до 1200°С при атмосферном давлении.
Коэффициент вязкости воздуха с ростом его температуры значительно увеличивается. Например, кинематическая вязкость воздуха равна 15,06·10-6 м2/с при температуре 20°С, а с ростом температуры до 1200°С вязкость воздуха становиться равной 233,7·10-6 м2/с, то есть увеличивается в 15,5 раз! Динамическая вязкость воздуха при температуре 20°С равна 18,1·10-6 Па·с.
При нагревании воздуха увеличиваются значения как кинематической, так и динамической вязкости. Эти две величины связаны между собой через величину плотности воздуха, значение которой уменьшается при нагревании этого газа. Увеличение кинематической и динамической вязкости воздуха (как и других газов) при нагреве связано с более интенсивным колебанием молекул воздуха вокруг их равновесного состояния (согласно МКТ).
| t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с |
|---|---|---|---|---|---|---|---|---|
| -50 | 14,6 | 9,23 | 70 | 20,6 | 20,02 | 350 | 31,4 | 55,46 |
| -45 | 14,9 | 9,64 | 80 | 21,1 | 21,09 | 400 | 33 | 63,09 |
| -40 | 15,2 | 10,04 | 90 | 21,5 | 22,1 | 450 | 34,6 | 69,28 |
| -35 | 15,5 | 10,42 | 100 | 21,9 | 23,13 | 500 | 36,2 | 79,38 |
| -30 | 15,7 | 10,8 | 110 | 22,4 | 24,3 | 550 | 37,7 | 88,14 |
| -25 | 16 | 11,21 | 120 | 22,8 | 25,45 | 600 | 39,1 | 96,89 |
| -20 | 16,2 | 11,61 | 130 | 23,3 | 26,63 | 650 | 40,5 | 106,15 |
| -15 | 16,5 | 12,02 | 140 | 23,7 | 27,8 | 700 | 41,8 | 115,4 |
| -10 | 16,7 | 12,43 | 150 | 24,1 | 28,95 | 750 | 43,1 | 125,1 |
| -5 | 17 | 12,86 | 160 | 24,5 | 30,09 | 800 | 44,3 | 134,8 |
| 0 | 17,2 | 13,28 | 170 | 24,9 | 31,29 | 850 | 45,5 | 145 |
| 10 | 17,6 | 14,16 | 180 | 25,3 | 32,49 | 900 | 46,7 | 155,1 |
| 15 | 17,9 | 14,61 | 190 | 25,7 | 33,67 | 950 | 47,9 | 166,1 |
| 20 | 18,1 | 15,06 | 200 | 26 | 34,85 | 1000 | 49 | 177,1 |
| 30 | 18,6 | 16 | 225 | 26,7 | 37,73 | 1050 | 50,1 | 188,2 |
| 40 | 19,1 | 16,96 | 250 | 27,4 | 40,61 | 1100 | 51,2 | 199,3 |
| 50 | 19,6 | 17,95 | 300 | 29,7 | 48,33 | 1150 | 52,4 | 216,5 |
| 60 | 20,1 | 18,97 | 325 | 30,6 | 51,9 | 1200 | 53,5 | 233,7 |
Примечание: Будьте внимательны! Вязкость воздуха дана в степени 106.
Удельная теплоемкость воздуха при температуре от -50 до 1200°С
Представлена таблица удельной теплоемкости воздуха при различных температурах. Теплоемкость в таблице дана при постоянном давлении (изобарная теплоемкость воздуха) в интервале температуры от минус 50 до 1200°С для воздуха в сухом состоянии. Чему равна удельная теплоемкость воздуха? Величина удельной теплоемкости определяет количество тепла, которое необходимо подвести к одному килограмму воздуха при постоянном давлении для увеличения его температуры на 1 градус. Например, при 20°С для нагревания 1 кг этого газа на 1°С в изобарном процессе, требуется подвести 1005 Дж тепла.
Удельная теплоемкость воздуха увеличивается с ростом его температуры. Однако, зависимость массовой теплоемкости воздуха от температуры не линейная. В интервале от -50 до 120°С ее величина практически не меняется — в этих условиях средняя теплоемкость воздуха равна 1010 Дж/(кг·град). По данным таблицы видно, что значительное влияние температура начинает оказывать со значения 130°С. Однако, температура воздуха влияет на его удельную теплоемкость намного слабее, чем на вязкость. Так, при нагреве с 0 до 1200°С теплоемкость воздуха увеличивается лишь в 1,2 раза – с 1005 до 1210 Дж/(кг·град).
Следует отметить, что теплоемкость влажного воздуха выше, чем сухого. Если сравнить теплоемкость воды и воздуха, то очевидно, что вода обладает более высоким ее значением и содержание воды в воздухе приводит к увеличению удельной теплоемкости.
| t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) |
|---|---|---|---|---|---|---|---|
| -50 | 1013 | 20 | 1005 | 150 | 1015 | 600 | 1114 |
| -45 | 1013 | 30 | 1005 | 160 | 1017 | 650 | 1125 |
| -40 | 1013 | 40 | 1005 | 170 | 1020 | 700 | 1135 |
| -35 | 1013 | 50 | 1005 | 180 | 1022 | 750 | 1146 |
| -30 | 1013 | 60 | 1005 | 190 | 1024 | 800 | 1156 |
| -25 | 1011 | 70 | 1009 | 200 | 1026 | 850 | 1164 |
| -20 | 1009 | 80 | 1009 | 250 | 1037 | 900 | 1172 |
| -15 | 1009 | 90 | 1009 | 300 | 1047 | 950 | 1179 |
| -10 | 1009 | 100 | 1009 | 350 | 1058 | 1000 | 1185 |
| -5 | 1007 | 110 | 1009 | 400 | 1068 | 1050 | 1191 |
| 0 | 1005 | 120 | 1009 | 450 | 1081 | 1100 | 1197 |
| 10 | 1005 | 130 | 1011 | 500 | 1093 | 1150 | 1204 |
| 15 | 1005 | 140 | 1013 | 550 | 1104 | 1200 | 1210 |
Теплопроводность, температуропроводность, число Прандтля воздуха
В таблице представлены такие физические свойства атмосферного воздуха, как теплопроводность, температуропроводность и его число Прандтля в зависимости от температуры. Теплофизические свойства воздуха даны в интервале от -50 до 1200°С для сухого воздуха. По данным таблицы видно, что указанные свойства воздуха существенно зависят от температуры и температурная зависимость рассмотренных свойств этого газа различна.
Теплопроводность воздуха λ при повышении температуры увеличивается во всем диапазоне, достигая при 1200°С величины 0,0915 Вт/(м·град). Другие теплофизические свойства воздуха такие, как его температуропроводность a и число Прандтля Pr, по-разному реагируют на изменение температуры. Температуропроводность, как и вязкость воздуха сильно зависит от температуры и при нагревании, например с 0 до 1200°С, ее значение увеличивается почти в 17 раз.
Число Прандтля воздуха слабо зависит от температуры и при нагревании этого газа его величина сначала снижается до величины 0,674, а затем начинает расти, и при температуре 1200°С достигает значения 0,724.
| t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr | t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr |
|---|---|---|---|---|---|---|---|
| -50 | 2,04 | 12,7 | 0,728 | 170 | 3,71 | 45,7 | 0,682 |
| -40 | 2,12 | 13,8 | 0,728 | 180 | 3,78 | 47,5 | 0,681 |
| -30 | 2,2 | 14,9 | 0,723 | 190 | 3,86 | 49,5 | 0,681 |
| -20 | 2,28 | 16,2 | 0,716 | 200 | 3,93 | 51,4 | 0,68 |
| -10 | 2,36 | 17,4 | 0,712 | 250 | 4,27 | 61 | 0,677 |
| 0 | 2,44 | 18,8 | 0,707 | 300 | 4,6 | 71,6 | 0,674 |
| 10 | 2,51 | 20 | 0,705 | 350 | 4,91 | 81,9 | 0,676 |
| 20 | 2,59 | 21,4 | 0,703 | 400 | 5,21 | 93,1 | 0,678 |
| 30 | 2,67 | 22,9 | 0,701 | 450 | 5,48 | 104,2 | 0,683 |
| 40 | 2,76 | 24,3 | 0,699 | 500 | 5,74 | 115,3 | 0,687 |
| 50 | 2,83 | 25,7 | 0,698 | 550 | 5,98 | 126,8 | 0,693 |
| 60 | 2,9 | 27,2 | 0,696 | 600 | 6,22 | 138,3 | 0,699 |
| 70 | 2,96 | 28,6 | 0,694 | 650 | 6,47 | 150,9 | 0,703 |
| 80 | 3,05 | 30,2 | 0,692 | 700 | 6,71 | 163,4 | 0,706 |
| 90 | 3,13 | 31,9 | 0,69 | 750 | 6,95 | 176,1 | 0,71 |
| 100 | 3,21 | 33,6 | 0,688 | 800 | 7,18 | 188,8 | 0,713 |
| 110 | 3,28 | 35,2 | 0,687 | 850 | 7,41 | 202,5 | 0,715 |
| 120 | 3,34 | 36,8 | 0,686 | 900 | 7,63 | 216,2 | 0,717 |
| 130 | 3,42 | 38,6 | 0,685 | 950 | 7,85 | 231,1 | 0,718 |
| 140 | 3,49 | 40,3 | 0,684 | 1000 | 8,07 | 245,9 | 0,719 |
| 150 | 3,57 | 42,1 | 0,683 | 1100 | 8,5 | 276,2 | 0,722 |
| 160 | 3,64 | 43,9 | 0,682 | 1200 | 9,15 | 316,5 | 0,724 |
Будьте внимательны! Теплопроводность воздуха в таблице указана в степени 102. Не забудьте разделить на 100! Температуропроводность воздуха указана в степени 106. Допускается интерполяция значений физических свойств воздуха в приведенных таблицах.
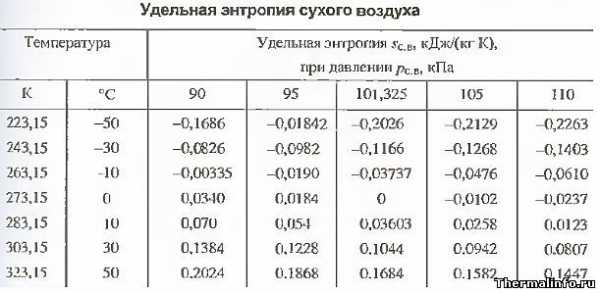
Энтропия сухого воздуха
В таблице представлены значения такого теплофизического свойства воздуха, как удельная энтропия. Значения энтропии даны для сухого воздуха в размерности кДж/(кг·град) в зависимости от температуры и давления. Удельная энтропия указана в таблице в интервале температуры от -50 до 50°С при давлении воздуха от 90 до 110 кПа. Следует отметить, что при нормальном атмосферном давлении (101,325 кПа) и температуре, например 30°С, удельная энтропия воздуха равна 0,1044 кДж/(кг·град).
 Источники:
Источники:
- Михеев М.А., Михеева И.М. Основы теплопередачи.
- Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная теника. Кондиционирование воздуха. Свойства веществ: Справ./ Под ред. С.Н. Богданова. 4-е изд., перераб. и доп. — СПб.: СПбГАХПТ, 1999.- 320 с.
thermalinfo.ru
Вязкость воды: таблицы при различных температурах
Кинематическая вязкость воды при различных температурах
Вода H2O представляет собой ньютоновскую жидкость и ее течение описывается законом вязкого трения Ньютона, в уравнении которого коэффициент пропорциональности называется коэффициентом вязкости, или просто вязкостью.
Вязкость воды зависит от температуры. Кинематическая вязкость воды равна 1,006·10-6 м2/с при температуре 20°С.
В таблице представлены значения кинематической вязкости воды в зависимости от температуры при атмосферном давлении (760 мм.рт.ст.). Значения вязкости даны в интервале температуры от 0 до 300°С. При температуре воды свыше 100°С, ее кинематическая вязкость указана в таблице на линии насыщения.
Кинематическая вязкость воды изменяет свою величину при нагревании и охлаждении. По данным таблицы видно, что с ростом температуры воды ее кинематическая вязкость уменьшается. Если сравнить вязкость воды при различных температурах, например при 0 и 300°С, то очевидно ее уменьшение примерно в 14 раз. То есть вода при нагревании становится менее вязкой, а высокая вязкость воды достигается если воду максимально охладить.
Значения коэффициента кинематической вязкости при различных температурах необходимы для вычисления величины числа Рейнольдса, которое соответствует определенному режиму течения жидкости или газа.
| t, °С | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 |
|---|---|---|---|---|---|---|---|---|
| ν·106, м2/с | 1,789 | 1,006 | 0,659 | 0,478 | 0,365 | 0,295 | 0,252 | 0,217 |
| t, °С | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 |
| ν·106, м2/с | 0,191 | 0,173 | 0,158 | 0,148 | 0,141 | 0,135 | 0,131 | 0,128 |
Если сравнить вязкость воды с вязкостью других ньютоновских жидкостей, например с кровью, или с маслами, то вода будет иметь меньшую вязкость. Менее вязкими, по сравнению с водой, являются органические жидкости – ацетон, бензол и сжиженные газы, например такие, как жидкий азот.
Динамическая вязкость воды в зависимости от температуры
Кинематическая и динамическая вязкость связаны между собой через значение плотности. Если кинематическую вязкость умножить на плотность, то получим величину коэффициента динамической вязкости (или просто динамическую вязкость).
Динамическая вязкость воды при температуре 20°С равна 1004·10-6 Па·с. В таблице даны значения коэффициента динамической вязкости воды в зависимости от температуры при нормальном атмосферном давлении (760 мм.рт.ст.). Вязкость в таблице указана при температуре от 0 до 300°С.
| t, °С | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 |
|---|---|---|---|---|---|---|---|---|
| μ·106, Па·с | 1788 | 1004 | 653,3 | 469,9 | 355,1 | 282,5 | 237,4 | 201,1 |
| t, °С | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 |
| μ·106, Па·с | 173,6 | 153,0 | 136,4 | 124,6 | 114,8 | 105,9 | 98,1 | 91,2 |
Динамическая вязкость при нагревании воды уменьшается, вода становится менее вязкой и при достижении температуры кипения 100°С величина вязкости воды составляет всего 282,5·10-6 Па·с.
Источник:
Михеев М. А., Михеева И. М. Основы теплопередачи.
thermalinfo.ru
Зависимость вязкости жидкостей от температуры и давления
Зависимость вязкости жидкости от температуры. . 311 Зависимость вязкости жидкости от давления. . . 314 Вязкость жидкостей, кипящих под повышенным давлением (область от нормальной температуры кипения до критической). ………..315 [c.279]Как известно [3], влияние давления на вязкость капельных жидкостей сказывается в области высоких давлений. Поэтому, в тех случаях, когда давление не превышает 10 МПа, изменением вязкости от давления пренебрегают. Вязкость, главным образом, зависит от рода жидкости и температуры (табл. 6 и 7). Обычно зависимость вязкости от температуры для различных жидкостей определяется по экспериментальным формулам, графикам, таблицам. [c.11]
ЗАВИСИМОСТЬ ВЯЗКОСТИ ЖИДКОСТИ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ [c.311] Изменение давления до 10 МПа мало влияет на изменение вязкости. При больших давлениях его влиянием на изменение вязкости пренебрегать нельзя. Аналитические зависимости вязкости от температуры весьма разнообразны. Отношение коэффициента динамической вязкости к плотности жидкости называется коэффициентом кинематической вязкости, который обычно и применяется в практических расчетах [c.18]
В жидкостях вязкость обусловлена преимущественно внутренним давлением, а в газах — тепловым движением молекул. Этим объясняется характер зависимости вязкости от температуры у жидкостей с повышением температуры вязкость уменьшается, так как при этом уменьшается внутреннее давление, а у газов — возрастает, поскольку при этом усиливается интенсивность перемещения молекул газа из слоя в слой. [c.33]
Некоторые исследователи [46, 103, 104] установили важную зависимость вязкости жидкостей и газов от плотности. Эта зависимость интересна потому, что дает возможность обоба е-ния данных по вязкости газов и жидкостей при различных температурах и давлениях. Особенность этой закономерности состоит в том, что если на одну из осей координат откладывать плотность р, а на другую—значение избыточной вязкости (ч1р.т — т), то экспериментальные данные для всех температур расположатся на одной кривой. [c.105]
На диаграмме в логарифмической системе координат по обеим осям зависимость вязкости жидкости от давления пара стандартной жидкости при одинаковых температурах должна, на основа- [c.293]
Вязкость газов также возрастает с повышением давления. Так, вязкость этилена при 1000 атм и 24° в 12 раз больше, чем при атмосферном давлении [55]. При небольших приведенных температурах и высоких давлениях вязкость газов может быть описана формулами, выражающими зависимость вязкости жидкостей от давления [56]. [c.119]
Методы приближенного расчета вязкости жидкости. . . 310 Зависимость вязкости жидкости от температуры и давления. ………………311 [c.279]
В этой главе рассматриваются вопросы учета сырой нефти при ее дальнейшей транспортировке, не затрагивая вопросов измерения дебита нефтяных скважин. Под сырой нефтью будем подразумевать любую нефть (жидкость), полученную после сепарации, без всякого ограничения содержания каких-либо примесей (воды, солей, механических примесей и т.д.) и перекачиваемую на установки подготовки нефти. Эта жидкость представляет собой сложную смесь нефти, растворенного газа, пластовой воды, содержащей, в свою очередь, различные соли, парафина, церезина и других веществ, механических примесе
www.chem21.info
Динамический коэффициент вязкости
Вязкостью называется способность жидкости сопротивляться относительному перемещению ее частиц при воздействии внешних сил, т.е. наличие вязкости обуславливает возникновение сил внутреннего трения в движущейся жидкости.
Вязкость характеризуется динамическим μ или кинематическим коэффициентами вязкости υ, связанными между собой соотношением:
Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.
Различают динамическую вязкость (единицы измерения: Па·с = 10 пуаз) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.
Переход вещества из жидкого состояния в стеклообразное обычно связывают с достижением вязкости порядка 1011−1012 Па·с
Прибор для измерения вязкости называется вискозиметром.
Сила вязкого трения F пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию междуплоскостями h:
Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости.
Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.
Влияние температуры на вязкость газов
В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).
Формула Сазерленда может быть использована для определения вязкости идеального газав зависимости от температуры:[1]
где:
μ = динамическая вязкость в (Па·с) при заданной температуре T,
μ0 = контрольная вязкость в (Па·с) при некоторой контрольной температуре T0,
T = заданная температура в Кельвинах,
T0 = контрольная температура в Кельвинах,
C = постоянная Сазерленда для того газа, вязкость которого требуется определить.
Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.
Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:
Коэффициент вязкости (динамическая вязкость) может быть получен на основе соображений о движениях молекул. Очевидно, что будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде:
Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение
где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.
Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.
Кинематическая вязкость
В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной
и эта величина получила название кинематической вязкости. Здесь — плотность жидкости; — динамическая вязкость (см. выше).
Кинематическая вязкость в старых источниках часто указана в сантистоксах (сСт). В СИ эта величина переводится следующим образом:
1 сСт = 1мм21c = 10−6 м2c
Пло́тность — скалярнаяфизическая величина, определяемая как отношениемассытела к занимаемому этим теломобъёмуилиплощади(поверхностная плотность). Более строгое определение плотности требует уточнение формулировки:
Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
Плотность вещества — это плотность тел, состоящих из этого вещества. Отсюда вытекает и короткая формулировка определения плотности вещества: плотность вещества — это масса его единичного объёма.
Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю[1], или, записывая кратко, . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемойфизической модели.
Исходя из определения плотности, её размерность кг/м³ в системе СИи в г/см³ в системеСГС.
Для сыпучих и пористых тел различают:
истинную плотность, определяемую без учёта пустот;
удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.
где М — молярная массагаза,—молярный объём(принормальных условияхравен 22,4 л/моль).
studfile.net
