Динамическая вязкость газов (уравнение Сазерленда) Калькулятор
✖Константа a — это эмпирическая константа, заданная в соответствии с условиями в уравнении Сазерленда.ⓘ Постоянный а [A] | +10% -10% | ||
✖Температура – это степень или интенсивность тепла, присутствующего в веществе или объекте.ⓘ Температура [T] | ЦельсияДелильФаренгейтКельвинНьютонРанкинтемпература по реомюруРёмерТройной точки воды | +10% -10% | |
✖b — эмпирическая константаⓘ б [b] | +10% -10% |
|
✖Динамическая вязкость жидкости — это мера ее сопротивления течению при приложении внешней силы.ⓘ Динамическая вязкость газов (уравнение Сазерленда) [μviscosity] |
|
⎘ копия |
👎
Формула
сбросить
👍
Динамическая вязкость газов (уравнение Сазерленда) Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. (1/2)))/(1+b/T)
(1/2)))/(1+b/T)
Связь между температурой и вязкостью?
По мере повышения температуры газы становятся более динамичными, больше столкновений приводит к большей передаче молекулярного импульса между разными слоями. Следовательно, с увеличением температуры увеличивается вязкость газов.
Share
Copied!
|
Заглавная страница
КАТЕГОРИИ: Археология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
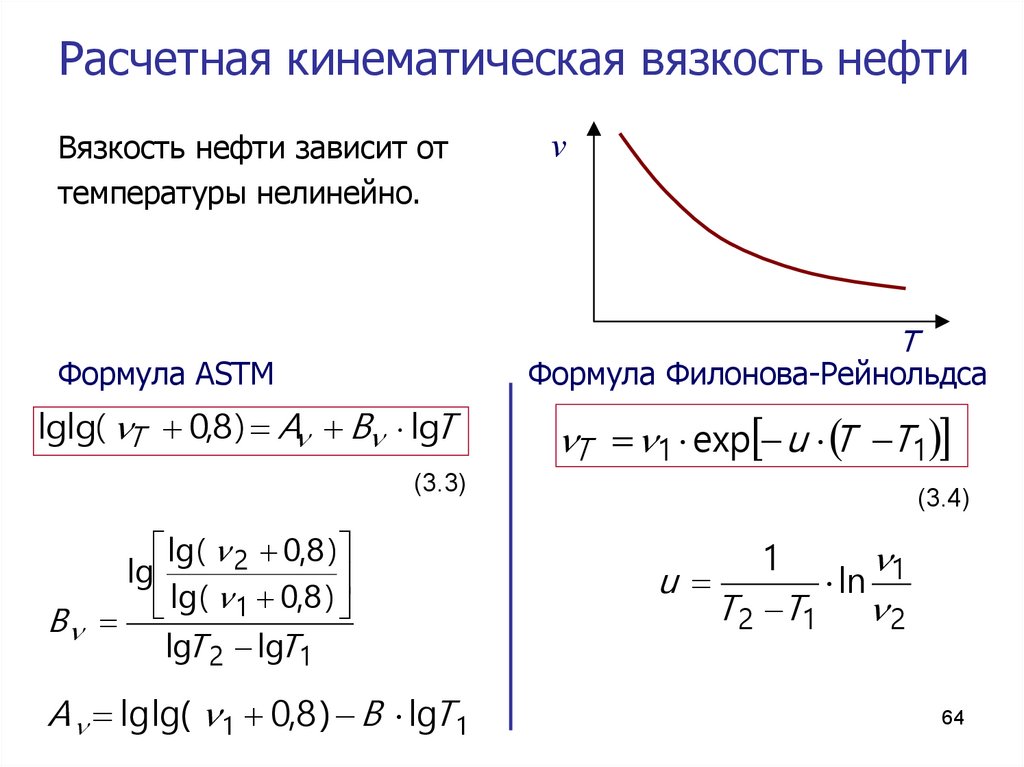
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒ В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры). Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:[1] где: · μ = динамическая вязкость в (Па·с) при заданной температуре T, · μ0 = контрольная вязкость в (Па·с) при некоторой контрольной температуре T0, · T = заданная температура в Кельвинах, · T0 = контрольная температура в Кельвинах, · C = постоянная Сазерленда для того газа, вязкость которого требуется определить. Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.
ВЯЗКОСТЬ ЖИДКОСТЕЙ Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона: Коэффициент вязкости — будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: Коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского. Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.
В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной и эта величина получила название кинематической вязкости. Здесь — плотность жидкости; — коэффициент динамической вязкости
Пусть имеются две параллельные пластинки, между которыми находится газ (жидкость). Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0. Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е. (3.3.1) Постоянная a определяется из условия, что при x = h u = u0, т. е. u0 = ah. (3.3.2) Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения. Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е. где – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения , равенство (3.3.3) перепишем в виде Так как из (3.3.2) следует, что , то последнее выражение можно представить так: Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Согласно второму закону Ньютона, , где K – импульс элементарной массы слоя газа. Поэтому формулу выше можно представить в виде бесконечно малых: Таким образом, с точки зрения молекулярно-кинетической теории в процесс внутреннего трения каждая молекула переносит упорядоченный импульс , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса и , получим: 7. Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры: где — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры).
В интегральной форме это же выражение запишется так где — полная мощность тепловых потерь, — площадь сечения параллелепипеда, — перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями. Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициент теплопроводности газов определяется формулой: Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. ВЫВОД ФОРМУЛ: Для количественного описания термодинамического потока вводят величину , численно равную количеству физической величины, переносимой за одну секунду через выбранную поверхность. В случае диффузии поток определяет интенсивность переноса частиц примеси; при теплопроводности величина численно равна количеству теплоты, переносимой за единицу времени; для явления вязкости величина характеризует перенос импульса. В общем случае поток определяется следующим образом: где: — плотность термодинамического потока, — вектор, численно равный величине элементарной поверхности и направленный по нормали к этой поверхности. Если термодинамический поток однороден и вектор во всех точках среды одинаков и перпендикулярен поверхности, то величина потока , проходящего через плоскую площадку , определяется по формуле: где — абсолютное значение (модуль) вектора . Если рассматриваемая термодинамическая система находится в состоянии, близком к равновесию, то плотность термодинамического потока пропорциональна градиенту соответствующей физической величины в той же точке: (6.3) где — коэффициенты переноса, или кинетические коэффициенты. Из выражения (6.3) следует, что плотность термодинамического потока имеет тем большую величину, чем сильнее изменяется физическая величина от точки к точке пространства. Кроме этого, знак минус в этом выражении указывает на то, что поток направлен в сторону уменьшения величины . Величина зависит от описываемого процесса. При описании диффузии в качестве параметра выступает относительная концентрация примеси, а коэффициент переноса представляет собой коэффициент диффузии . Для случая теплопроводности вместо необходимо использовать энергию теплового движения молекулы, а коэффициент является коэффициентом теплопроводности . Параметром при описании вязкости будет импульс упорядоченного движения молекулы, а величина — это коэффициент вязкости . В случае если величина зависит только от одной пространственной переменной (случай одномерной среды), формула (6.3) приобретает более простой вид: или для потока : 8. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества.
Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний. Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений. Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими. Уравнение идеального газа в отношении его давления записывается обычно в виде В этом выражении Rg— универсальная газовая постоянная, а T — температура и r-плотность. Изотермический процесс процесс изменения состояния термодинамической системы при постоянной температуре ( )( ). Изотермический процесс описывается законом Бойля — Мариотта: При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const. Изохорный процесс процесс изменения состояния термодинамической системы при постоянном объёме ( ). Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления, а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание. Изобарный процесс процесс изменения состояния термодинамической системы при постоянном давлении ( ) Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const. Параметры состояния Вещества обычно пребывают в одном из трех основных состояний: в виде газа, жидкости или твердого тела . Свойства вещества могут быть интенсивными и экстенсивными. Интенсивными называют свойства, не зависящие от количества вещества в системе (давление, температура и некоторые другие). Примером экстенсивных свойств является объем, который изменяется в данных условиях пропорционально количеству вещества: объем 10 кг вещества будет в 10 раз больше, чем объем 1 кг. Удельные, т. е. отнесенные к массе вещества, экстенсивные свойства приобретают смысл интенсивных свойств. Так, удельный объем, удельная теплоемкость и т. п. могут рассматриваться как интенсивные свойства. Интенсивные свойства, определяющие состояние тела или группы тел — термодинамической системы — называют термодинамическими параметрами состояния тела (системы). Наиболее удобными и поэтому наиболее распространенными параметрами состояния являются абсолютная температура, абсолютное давление и удельный объем (или плотность) тела. Одним из важнейших параметров является абсолютная температура. Температура характеризует тепловое состояние тела. Как хорошо известно из опыта, теплота может самопроизвольно переходить лишь от более нагретых тел к менее нагретым, т. е. от тел с большей температурой к телам с меньшей температурой. Таким образом, температуры тел определяют направление возможного самопроизвольного перехода теплоты между этими телами .
⇐ Предыдущая123456Следующая ⇒ Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 3959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Закон Сазерленда
Закон СазерлендаЗакон Сазерленда
Закон Сазерленда, или формула Сазерленда, является приближенным представлением того, как вязкость газов зависит от температуры. Этот закон основан на идеализированном потенциале межмолекулярных сил и гласит (ссылка 5)
.(6-7)
, где Sμ — эффективная температура, называемая постоянной Сазерленда. Каждый газ имеет свою постоянную Сазерленда. Уравнение 6-7 строго справедливо только для однокомпонентных газов при низком давлении. Однако он хорошо работает с воздухом, потому что воздух в основном состоит из азота и кислорода, которые имеют очень похожие свойства. Значения параметров для некоторых распространенных газов приведены в таблице 6-2 (ссылка 5).
Газ | мк0 | Т0 | Sμ |
Воздух | 1,716·10-5 | 273 | 111 |
Аргон | 2,125·10-5 | 273 | 114 |
С02 | 1.370·10-5 | 273 | 222 |
СО | 1,657·10-5 | 273 | 136 |
Н2 | 1,663·10-5 | 273 | 107 |
О2 | 1,919·10-5 | 273 | 139 |
ч3 | 8. | 273 | 97 |
пар | 1,12·10-5 | 350 | 1064 |
Единица СИ для μ0 в Таблице 6-2 – Н·с/м2. Единицей СИ для T0 и Sμ является кельвин (К).
Закон Сазерленда можно также сформулировать для теплопроводности (ссылка 5):
(6-8)
Значения k0, T0 и Sk для некоторых распространенных газов приведены в таблице 6-3 (ссылка 5).
Газ | к0 | Т0 | С,к |
Воздух | 0,0241 | 273 К | 194 |
Аргон | 0,0163 | 273 | 170 |
С02 | 0,0146 | 273 | 1800 |
СО | 0,0232 | 273 | 180 |
Н2 | 0,0242 | 273 | 150 |
О2 | 0,0244 | 273 | 240 |
ч3 | 0,168 | 273 | 120 |
пар | 0,0181 | 300 | 2200 |
Единицей измерения k0 в таблице 6-3 является Вт/(м·K).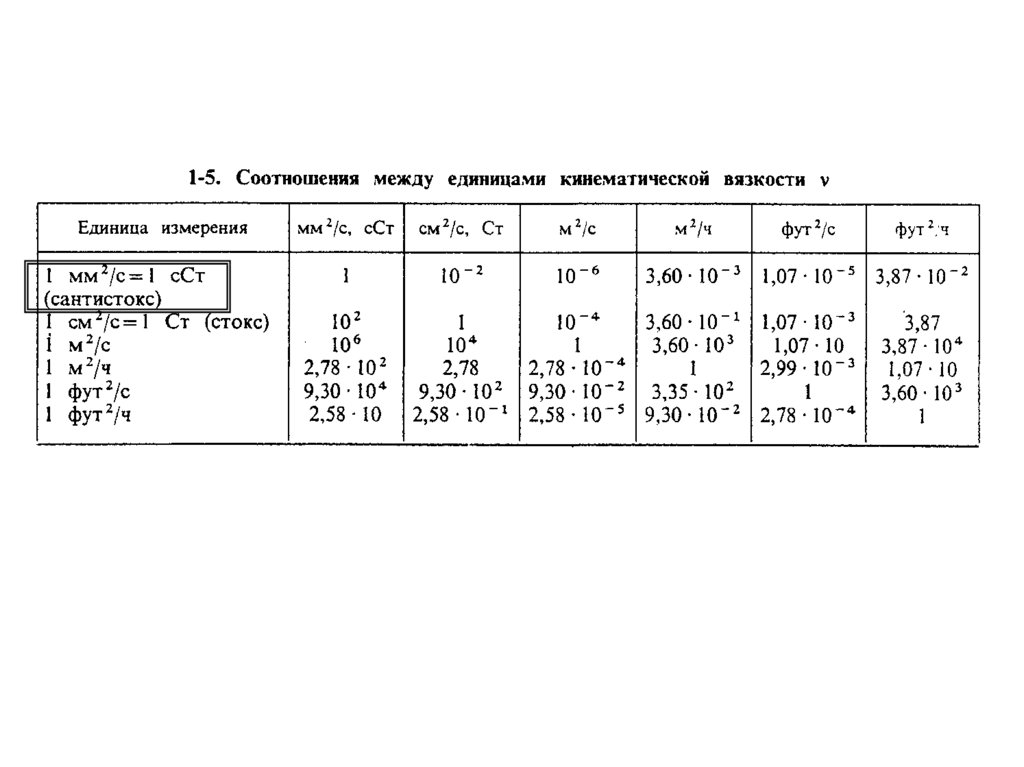 Единицей для T0 и Sk является кельвин (K).
Единицей для T0 и Sk является кельвин (K).
Закон Сазерленда
При работе над практическими инженерными приложениями часто возникают проблемы, связанные со значительными изменениями температуры локально в поле течения. Например, если вы выполняете расчет теплопередачи, вы обычно хотите использовать 9Пленка 0363 свойства (она же свойства, примыкающие к стене). Для этого в любом практическом смысле требуется модель вязкости и теплопроводности.
Для чистого не вступающего в реакцию газа вязкость зависит только от температуры (Anderson 2006). Следовательно, вязкость можно моделировать, используя только температуру. Одна из этих моделей, которая встроена в такое программное обеспечение, как OpenFOAM, — это закон Сазерленда.
Задается как:
Также часто упрощается (как в OpenFOAM) до:
В правой части указаны обозначения OpenFOAM. Для воздуха,
, .
Коэффициенты для нескольких других газов можно найти в книге Фрэнка Уайта «Поток вязкой жидкости» (2006).
Когда это применимо?
Это важный вопрос. Если вы занимаетесь инженерией или исследованиями, вы должны знать пределы этих уравнений. Согласно Андерсону (2006), «закон Сазерленда точен для воздуха в диапазоне нескольких тысяч градусов и, безусловно, подходит для гиперзвуковых расчетов вязкого течения». В важнейшем учебнике для студентов Фрэнка Уайта говорится, что он «адекватен в широком диапазоне температур».
Для воздуха в другом источнике (Rathakrishnan 2013) утверждается, что соотношение действует от 0,01 до 100 атм и от 0 до 3000K. А в «Потоке вязкой жидкости» Фрэнка Уайта упоминается ошибка 2% между 170K и 1900K для воздуха.
Что делать, если вы не можете найти коэффициенты?
Если вы не можете найти хороший справочник с перечнем коэффициентов газа, который вы ищете, один из вариантов — перейти к веб-книге NIST, загрузить 2 значения вязкости при двух разных температурах и найти 2 коэффициента. Или подобрать кривую в Matlab, используя ряд данных из NIST или какого-либо другого источника.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления


 Откуда a = u0/h. Тогда выражение (3.3.1) примет вид
Откуда a = u0/h. Тогда выражение (3.3.1) примет вид Физический смысл коэффициента вязкости заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости
Физический смысл коэффициента вязкости заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости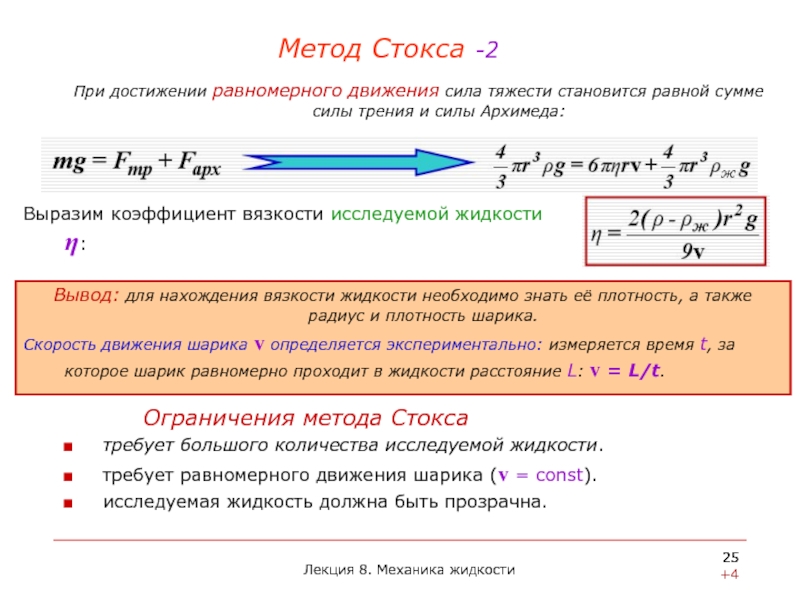 (количественная характеристика способности конкретного вещества проводить тепло)
(количественная характеристика способности конкретного вещества проводить тепло) Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные.
Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные.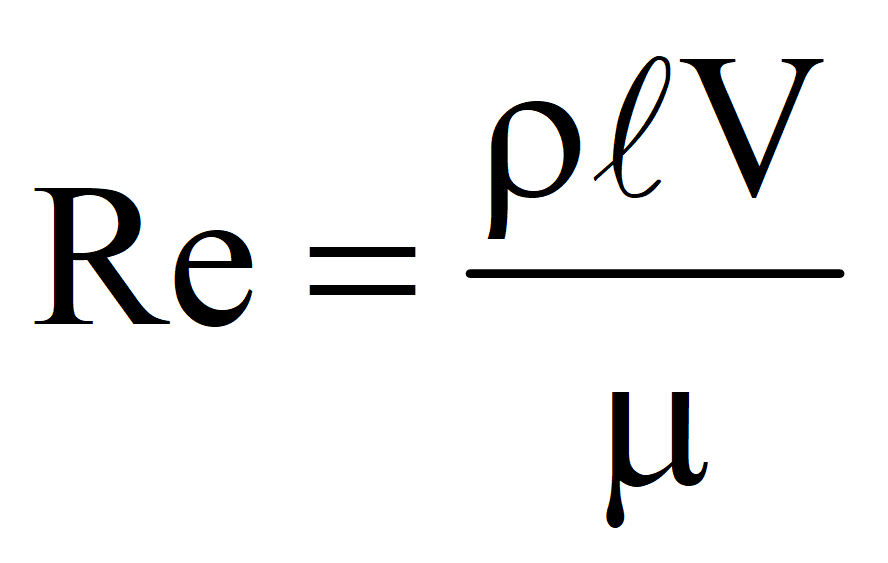

 Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.
Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.
Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.
 Закон Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
Закон Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре: Очевидно, что одно и то же тело, одно и то же вещество при разных условиях может находиться в различных состояниях. В заданных неизменных условиях рассматриваемое вещество всегда будет находиться в одном и том же состоянии, например при атмосферном давлении и температуре 400 °С вода будет существовать только в виде пара, но никак не в виде жидкости или твердого вещества.
Очевидно, что одно и то же тело, одно и то же вещество при разных условиях может находиться в различных состояниях. В заданных неизменных условиях рассматриваемое вещество всегда будет находиться в одном и том же состоянии, например при атмосферном давлении и температуре 400 °С вода будет существовать только в виде пара, но никак не в виде жидкости или твердого вещества.
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.02 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 38.242.236.216 (0.02 с.) 411·10-5
411·10-5