Что значит натуральное число: Натуральные числа: определение, примеры, свойства

Что такое натуральное число? Ответ на webmath.ru

Содержание:

Определение натурального числа

Определение

Натуральными числами называются числа, которые используются при счете или для указания порядкового номера предмета среди однородных предметов.

Например. Натуральными будут такие числа: $2,37,145,1059,24411$

Натуральные числа, записанные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурально числа 1. Множество всех натуральных чисел обозначают $N=\{1,2,3, \dots n, \ldots\}$. Оно бесконечно, так как не существует наибольшего натурального числа. Если к любому натуральному числу прибавить единицу, то получаем натуральное число, следующее за данным числом.

Пример

Задание. Какие из следующих чисел являются натуральными?

$$-89 ; 7 ; \frac{4}{3} ; 34 ; 2 ; 11 ; 3,2 ; \sqrt[3]{129} ; \sqrt{5}$$

Ответ.

$7 ; 34 ; 2 ; 11$

На множестве натуральных чисел вводится две основные арифметические операции — сложение и умножение. Для обозначения этих операций используются соответственно символы » + « и » • « (или » × «).

Сложение натуральных чисел

Каждой паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $s$, называемое суммой. Сумма $s$ состоит из стольких единиц, сколько их содержится в числах $n$ и $m$. О числе $s$ говорят, что оно получено в результате сложения чисел $n$ и $m$, и пишут

$$n+m=s$$

Числа $n$ и $m$ называются при этом слагаемыми. Операция сложения натуральных чисел обладает следующими свойствами:

1. Коммутативность: $n+m=m+n$
2. Ассоциативность: $(n+m)+k=n+(m+k)$

Подробнее о сложении чисел читайте по ссылке.

Слишком сложно?

Что такое натуральное число не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Найти сумму чисел:

$13+9 \quad$ и $ \quad 27+(3+72)$

Решение. $13+9=22$

Для вычисления второй суммы, для упрощения вычислений, применим к ней вначале свойство ассоциативности сложения:

$$27+(3+72)=(27+3)+72=30+72=102$$

Ответ. $13+9=22 \quad;\quad 27+(3+72)=102$

Умножение натуральных чисел

Каждой упорядоченной паре натуральных чисел $n$ и $m$ ставится в соответствие натуральное число $r$, называемое их произведением. Произведение $r$ содержит стольких единиц, сколько их содержится в числе $n$, взятых столько раз, сколько единиц содержится в числе $m$. О числе $r$ говорят, что оно получено в результате умножения чисел $n$ и $m$, и пишут

$n \cdot m=r \quad $ или $ \quad n \times m=r$

Числа $n$ и $m$ называются множителями или сомножителями.

Операция умножения натуральных чисел обладает следующими свойствами:

1. Коммутативность: $n \cdot m=m \cdot n$
2. Ассоциативность: $(n \cdot m) \cdot k=n \cdot(m \cdot k)$

Подробнее о умножении чисел читайте по ссылке.

Пример

Задание. Найти произведение чисел:

12$\cdot 3 \quad $ и $ \quad 7 \cdot 25 \cdot 4$

Решение. По определению операции умножения:

$$12 \cdot 3=12+12+12=36$$

Ко второму произведению применим свойство ассоциативности умножения:

$$7 \cdot 25 \cdot 4=7 \cdot(25 \cdot 4)=7 \cdot 100=700$$

Ответ. $12 \cdot 3=36 \quad;\quad 7 \cdot 25 \cdot 4=700$

Операция сложения и умножения натуральных чисел связаны законом дистрибутивности умножения относительно сложения:

$$(n+m) \cdot k=n \cdot k+m \cdot k$$

Сумма и произведение любых двух натуральных чисел всегда есть число натуральное, поэтому множество всех натуральных чисел замкнуто относительно операций сложения и умножения.

Так же на множестве натуральных чисел можно ввести операции вычитания и деления, как операции обратные к операциям сложения и умножения соответственно. Но эти операции не будут однозначно определенны для любой пары натуральных чисел. {5}=32$

Читать дальше: что такое рациональное число.

Что такое натуральное число?

Натуральное число, которое также можно назвать счетным числом, представлено цифрами от 1, 2, 3 до бесконечности. Число 0 включено, если натуральные числа определены как неотрицательные целые числа, но не если они определены как только положительные целые числа. В математике должно быть бесконечное количество цифр натурального числа, поскольку каждое натуральное число частично определяется наличием числа, следующего за ним. Эти числа также являются целыми числами, а не дробями или десятичными знаками, и могут использоваться для подсчета или упорядочения.

Основное различие между натуральным числом и целым числом состоит в том, что натуральные числа, за исключением нуля, являются только положительными. Там нет числа ниже нуля, и натуральное число не может сопровождаться нулем, как в случае с -1,0. По сути, это определяет натуральные числа как что-либо ноль или выше, что является целым, а не дробным. Ноль, как правило, считается единственным натуральным числом, которое не является положительным.

Понятие нуля развилось задолго после того, как цивилизации начали использовать подсчет чисел. Самые ранние записи о подсчете чисел с 1 по 10 более 4000 лет назад, когда вавилоняне использовали конкретный письменный код для обозначения места. Египтяне написали иероглифы для каждой цифры, но только около 1000 г. до н.э. концепция ноля была создана цивилизациями майя и ольмеков.

Хотя группы ольмеков и майя показывают первые записи об использовании ноля, концепция ноля также была разработана в Индии, в 7-м веке до нашей эры. Это было использование индейцев, а не мезоамериканское использование, которое было принято цивилизациями, как греки.

Существует много способов использования натуральных чисел в математических приложениях. Они могут ограничить проблемы, предполагая, что ответ должен быть натуральным числом. Они также изучаются в конкретных приложениях в теории множеств, математике, которая оценивает множества вещей. Теория чисел может оценивать натуральные числа как часть набора целых чисел или независимо друг от друга, чтобы увидеть, ведут ли они себя определенным образом или обладают определенными свойствами.

Возможно, одно из самых широких применений натуральных чисел приходит к нам очень «естественно». Когда мы молоды, мы учимся считать с 0 лет. Даже маленькие дети могут легко начать понимать разницу между одним и двумя или объяснить, сколько им лет. Это исследование продолжается, когда дети начинают ходить в школу и учатся манипулировать натуральными числами, умножать, делить, складывать и вычитать их. Только после того, как концепция натуральных чисел изучена, вводится концепция целых чисел, и возможность отрицательных чисел, которые могут сначала запутать некоторых детей, обычно изучается в четвертом или пятом классе не раньше.

ДРУГИЕ ЯЗЫКИ

Что такое натуральное значение числа. Натуральные числа в смысле количества предметов

Простейшее число — это натуральное число . Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.

Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.

Натуральные числа — это числа, начиная с единицы. Они образуются естественным образом при счёте. Например, 1,2,3,4,5… — первые натуральные числа.

Наименьшее натуральное число — один. Наибольшего натурального числа не существует. При счёте число ноль не используют, поэтому ноль натуральное число.

Натуральный ряд чисел — это последовательность всех натуральных чисел. Запись натуральных чисел:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

В натуральном ряду каждое число больше предыдущего на единицу.

Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.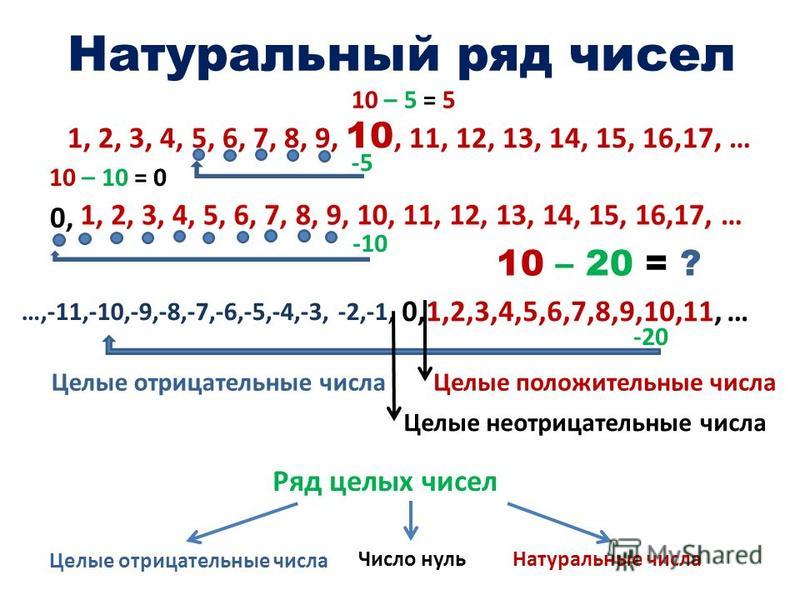

Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.

Классы натуральных чисел.

Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Для чтения натуральных чисел их разбивают, начиная справа, на группы по 3 цифры в каждой. 3 первые цифры справа — это класс единиц, 3 следующие — это класс тысяч, далее классы миллионов, миллиардов и так далее. Каждая из цифр класса называется его разрядом .

Сравнение натуральных чисел.

Из 2-х натуральных чисел меньше то число, которое при счете называется ранее. Например , число 7 меньше 11 (записывают так: 7 ). Когда одно число больше второго, это записывают так: 386 > 99 .

Таблица разрядов и классов чисел.

1-й класс единицы	1-й разряд единицы 2-й разряд десятки 3-й разряд сотни
2-й класс тысячи	1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч
3-й класс миллионы	1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов
4-й класс миллиарды	1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов

Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы. Основные свойства натуральных чисел. Коммутативность сложения. a + b = b + a Коммутативность умножения. ab = ba Ассоциативность сложения. (a + b) + c = a + (b + c) Ассоциативность умножения. Дистрибутивность умножения относительно сложения: Действия над натуральными числами. 4. Деление натуральных чисел — операция, обратная операции умножения. Если b ∙ с = а , то Формулы для деления: а: 1 = a a: a = 1, a ≠ 0 0: a = 0, a ≠ 0 (а ∙ b) : c = (a:c) ∙ b (а ∙ b) : c = (b:c) ∙ a Числовые выражения и числовые равенства. Запись, где числа соединяются знаками действий, является числовым выражением . Например, 10∙3+4; (60-2∙5):10. Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами . У равенства есть левая и правая части. Порядок выполнения арифметических действий. Сложение и вычитание чисел — это действия первой степени, а умножение и деление — это действия второй степени. Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо. Когда выражения состоят из действия только первой и второй степени, то сначала выполняют действия второй степени, а потом — действия первой степени. Когда в выражении есть скобки — сначала выполняют действия в скобках. Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.

Натуральные числа – натуральные числа это числа которые используются для счета предметов. Множество всех натуральных чисел иногда называют натуральным рядом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, и т. д.

Для записи натуральных чисел используют десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью них, можно записать любое натуральное число. Такая запись чисел называется десятичной.

Натуральный ряд чисел можно продолжать бесконечно. Нет такого числа, которые было бы последнее, потому что к последнему числу всегда можно прибавить единицу и получится число, уже большее искомого. В таком случае говорят, что в натуральном ряду нет наибольшего числа.

Разряды натуральных чисел

В записи любого числа с помощью цифр, место на котором цифра стоит в числе имеет решающее значение. Например, цифра 3 означает: 3 единицы, если она будет стоять в числе на последнем месте; 3 десятка, если она будет стоять в числе на предпоследнем месте; 4 сотни, если она будет стоять в числе на третьем месте с конца.

Последняя цифра означает разряд единиц, предпоследняя – разряд десятков, 3 с конца –разряд сотен.

Однозначные и многозначные цифры

Если в каком-либо разряде числа стоит цифра 0, это означает, что в данном разряде нет единиц.

С помощью цифры 0 обозначается число ноль. Ноль это «ни одного».

Нуль не относится к натуральным числам. Хотя некоторые математики считаю иначе.

Если число состоит из одной цифры его называют однозначным, из двух – двузначным, из трех – трехзначными, и т.д.

Числа которые не являются однозначными еще называют многозначными.

Классы из цифр для чтения больших натуральных чисел

Для чтения больших натуральных чисел, число разбивают на группы из трех цифр, начиная с правого края. Эти группы называются классы.

Первые три цифры с правого края составляют класс единиц, следующие три – класс тысяч, следующие три – класс миллионов.

Миллион – тысяча тысяч, для записи используют сокращение млн. 1 млн. = 1 000 000.

Миллиард = это тысяча миллионов. Для записи используют сокращение млрд. 1 млрд. = 1 000 000 000.

Пример записи и чтения

Это число имеет в классе миллиардов 15 единиц, 389 единиц в классе миллионов, нуль единиц в классе тысяч и 286 единиц в ласе единиц.

Данное число читается так: 15 миллиардов 389 миллионов 286.

Читают числа слева направо. По очереди называют число единиц каждого класса и потом добавляют название класса.

Натуральные числа

Натуральные числа – это те числа, которые применяются для подсчета различных предметов или для того, чтобы указать порядковый номер какого-либо предмета среди себе подобных или однородных.

Записывать натуральные числа можно с помощью первых десяти цифр:

Для записи простых натуральных чисел принято использовать позиционную десятичную систему исчисления, где значение любой цифры определяют ее местом в записи.

Натуральные числа – это простейшие числа, часто используемые нами в повседневной жизни. С помощью этих чисел мы ведем подсчеты, считаем предметы, определяем их количество, порядок и номер.

С натуральными числами мы начинаем знакомиться с самого раннего детства, поэтому они для каждого из нас являются привычными и естественными.

Общее представление о натуральных числах

Натуральные числа предназначены для несения информации о количестве предметов, их порядковом номере и множестве предметов.

Человек использует натуральные числа, так как они ему доступны как на уровне восприятия, так и на уровне воспроизведения. При озвучивании любого натурального числа, мы с вами легко его улавливаем на слух, а изобразив натуральное число – мы его видим.

Все натуральные числа располагаются в порядке возрастания и образуют числовой ряд, начинающийся с наименьшего натурального числа, которым является единица.

Если мы определились с наименьшим натуральным числом, то с наибольшим будет посложнее, так как такого числа не существует потому, что ряд натуральных чисел является бесконечным.

При прибавлении к натуральному числу единицы, в итоге мы получим число, которое идет за данным числом.

Такая цифра, как 0 не есть натуральным числом, а только служит для обозначения числа «ноль» и значит «ни одного». 0 означает отсутствие в десятичной записи чисел единиц данного ряда.

Все натуральные числа обозначаются заглавной латинской буквой N.

Историческая справка обозначения натуральных чисел

В древние времена человек еще не знал, что такое число и как можно посчитать количество предметов. Но уже тогда возникла необходимость в счете, и человек придумал, как можно сосчитать пойманную рыбу, собранные ягоды и т.д.

Немного позже, древний человек пришел к тому, что нужное ему количество проще записать. Для этих целей первобытные люди стали использовать камешки, а потом палочки, которые сбереглись в римских цифрах.

Следующим моментом развития системы исчисления стало использование в обозначениях некоторых чисел букв алфавита.

К первым системам исчисления относится десятичная индийская система и шестидесятеричная вавилонская.

Современная система исчисления, хоть и называется арабской, но, по сути, представляет один из вариантов индийской. Правда в ее системе исчисления отсутствует цифра ноль, но арабы ее добавили, и система приобрела нынешний вид.

Десятичная система исчисления

С натуральными числами мы уже познакомись и научились записывать их с помощью десяти цифр. Также вам уже известно, что запись чисел с использованием знаков, называется системой исчисления.

Значение цифры в записи числа зависит от ее позиции и называется позиционным. То есть, при методах записи натуральных чисел, мы используем позиционную систему исчисления.

Данная система основывается на разрядности и десятичности. В десятичной системе исчисления основой для ее построения будут цифры от 0 до 9.

Особое место в такой системе отводится числу 10, так как, в основном счет ведется десятками.

Таблица классов и разрядов:

Так, например, 10 единиц объединены в десятки, далее в сотни, тысячи и тому подобное. Поэтому число 10 является основанием системы исчисления и носит название десятичной системы исчисления.

Числа: натуральные, целые, рациональные, иррациональные, действительные, комплексные

Тестирование онлайн

• Округление чисел

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби . Например,

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Рассмотрим число 8,759123… . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.

Округлить 8,759123… с точностью до целой части.

Округлить 8,759123… с точностью до десятой части.

Округлить 8,759123… с точностью до сотой части.

Округлить 8,759123… с точностью до тысячной части.

Ненатуральные числа. Как отличить натуральные от ненатуральных

Что же такое натуральные и ненатуральные числа? Как объяснить ребенку, а может и не ребенку, в чем же отличия между ними? Давайте разбираться. Насколько известно, ненатуральные и натуральны числа изучают в 5 классе, и нашей целью является объяснить ученикам так, чтобы они действительно поняли и усвоили, что и как.

История

Натуральные числа — это одно из давних понятий. Давным-давно, когда люди еще не умели считать и не имели понятия о числах, когда им требовалось что-либо пересчитать, к примеру, рыбу, животных, они выбивали на различных предметах точечки или черточки, как это позже выяснилось археологами. В то время им было очень тяжело жить, но цивилизация развилась сначала до римской системы счисления, а затем до десятичной системы счисления. Сейчас же почти все используют арабские цифры

Все о натуральных числах

Натуральные числа — это простые числа, которыми мы пользуемся в повседневной нашей жизни для подсчета предметов для того, чтобы определить количество и порядок. В настоящее время для записи чисел мы используем десятичную систему счисления. Для того чтобы записать любое число, мы используем десять цифр — от нуля до девяти.

Натуральные числа — это те числа, которые мы используем при счете предметов или указании порядкового номера чего-либо. Пример: 5, 368, 99, 3684.

Числовым рядом называют натуральные числа, которые расположены в порядке возрастания, т.е. от единицы до бесконечности. Такой ряд начинается с наименьшего числа — 1, а наибольшего натурального числа не бывает, так как ряд чисел просто бесконечен.

Вообще, ноль — натуральным числом не считается, так как он означает отсутствие чего-либо, и счет предметов так же отсутствует

Арабская система счисления — это современная система, которой мы пользуемся каждый день. Она является одним из вариантов индийской (десятичной).

Такая система счисления стала современной из-за цифры 0, которую и изобрели арабы. До этого в индийской системе она отсутствовала.

Ненатуральные числа. Что это?

К натуральным числам не относятся отрицательные числа и нецелые. Значит, они и есть — ненатуральные числа

Ниже приведены примеры.

Ненатуральные числа бывают:

• Отрицательные числа, например: -1, -5, -36.. и так далее.
• Рациональные числа, которые выражены десятичными дробями: 4,5, -67, 44,6.
• В виде простой дроби: 1/2, 40 2/7 и т.д.
• Иррациональные числ, такие, как e = 2,71828, √2 = 1,41421 и тому подобное.

Мы надеемся, что очень помогли вам разобраться с ненатуральными и натуральными числами. Теперь вам станет легче объяснить своему малышу данную тему, и он усвоит ее так же хорошо, как великие математики!

Математика для блондинок: Натуральные числа

Определения натуральных чисел, которые приводятся в Википедии и математической литературе, возможно, кому-то не совсем понятны. Наверное, многие задают вопрос: «Натуральные числа — это какие?».

Для того, чтобы понимать, какие числа в математике называются натуральными, могу предложить такой вариант распознания натуральных чисел: единица и все числа, которые можно получить в результате сложения единиц, будут натуральными числами.

Если кто-то считает, что нуль принадлежит к натуральным числам, ничего страшного. Просто выучите наизусть, что ноль является натуральным числом и всё. В разных странах этот вопрос решается по-разному. Например, в англоязычной математике ноль считается натуральным числом. Спросите у любого шпиона))) Кстати, разведчики точно также могут проколоться на этом вопросе)))

Что мы сделали? Мы счетные палочки в руке заменили единичками в математике. Теперь проверим на практике, как это работает. Рассмотрим число 2 (два):

1 + 1 = 2

Число 2 является натуральным числом, так как может быть представлено в виде суммы двух единиц, что соответствует двум счетным палочкам или двум другим предметам «для счета естественным образом» (цитата из классического определения натуральных чисел).

Возьмем пример по сложнее. Если дробное число 7,5 разделить на другое дробное число 2,5, будет ли результат натуральным числом?

7,5 : 2,5 = 3

Да, в результате деления двух дробных чисел мы получили натуральное число 3, поскольку оно может быть получено в результате сложения трех единиц.

1 + 1 + 1 = 3

Если число рассыпается на единички без шума и пыли, такое число является натуральным. Например, число 2,5 (два с половиной) не является натуральным, так как кроме двух единичек со страшным грохотом отваливается дробная часть числа 0,5:

1 + 1 + 0,5 = 2,5

Еще один пример. Число -4 (минус четыре) не является натуральным, поскольку при разложении на единички отпадает знак минус и поднимает целую кучу пыли. Отрицательные числа невозможно получить сложением положительных единиц. Кстати, в пыли отрицательных чисел математики блуждали, как ежики в тумане. Вместо того, чтобы разобраться в причинах пылевой бури, они придумали модуль числа, чем еще больше всех запутали.

Надеюсь, мое пояснение поможет вам лучше ориентироваться в таких разных названиях таких одинаковых чисел.

Может ли дробное число быть натуральным? — нет, дробные числа не относятся к натуральным числам.

Хочу все знать: Натуральные числа и шкалы

ЧТО ЭТО? ЦИФРЫ ИЛИ ЧИСЛА?  

Аргументируй свой ответ.

ЧТО ТАКОЕ ЦИФРЫ?

Ци́фры (от ср. -лат. cifra от араб. صفر‎ (ṣifr) «пустой, нуль») — система знаков для записи конкретных значений чисел. Цифры нужны для записи чисел (как буквы для записи слов). Цифр 10, а чисел составить их этих десяти цифр можно бесконечное множество.

ВОПРОС

Можно ли назвать самое большое число? Почему?

ЧТО ТАКОЕ ЧИСЛО?

Число — это основное математическое понятие. Числа записывают с помощью комбинаций цифр. Число используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

ВОПРОСЫ-ЗАДАНИЯ

Приведи примеры разных чисел. 

Какими числами считают предметы? ПРиведи примеры.

Как вы понимаете слово «натуральный»?

НАТУРАЛЬНЫЕ ЧИСЛА

Есть числа, которые люди используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка. Такие числа называют натуральными.

С какого числа начинается счет?

Натуральные числа — это числа, начиная с единицы. Они образуются естественным образом при счёте. Например, 1,2,3,4,5… – первые натуральные числа.

Наименьшее натуральное число — один. Наибольшего натурального числа не существует. При счёте число ноль не используют, поэтому ноль НЕ натуральное число. 

Натуральный ряд чисел — это последовательность всех натуральных чисел. Запись натуральных чисел:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …

В натуральном ряду каждое число больше предыдущего на единицу.

Как обозначают множество натуральных чисел?

Множество всех натуральных чисел принято обозначать символом N (от лат. naturalis — естественный). 

Сколько чисел в натуральном ряду? 

Натуральный ряд бесконечен, самого большого натурального числа не существует.

В какой системе больше всего считает человек?

В десятичной позиционной. Видимо, десять пальцев на руке сложили такую систему исторически. Но есть и другие системы счисления. Подумай, какая система счисления используется в часах? Когда 12=1? Когда 7=1? Когда 2=1?

Как называются числа по количеству цифр в записи?

Расскажи, какие числа называют однозначными, двузначными, пятизначными, многозначными?

В многозначном числе каждая цифра занимает строго определенную позицию, которую называют разрядом числа.

Разряды многозначных чисел

Разряды чисел отсчитывают с его конца.

РОЛИК 1

РОЛИК 2

РОЛИК 3

Ряд натуральных чисел

УРОК ДЛЯ ПРОДВИНУТОГО КЛАССА 

Натуральный ряд чисел и его свойства. 

Изображение натуральных чисел точками на числовой прямой

ТРЕНАЖЕР 1

Соедини названия чисел с записью числа.

Натуральное число: определение и примеры

Определения статистики> Натуральные и целые числа

Содержание (Щелкните, чтобы перейти к этому разделу)

1. Натуральное число
2. Целые числа
3. Почему натуральное число — это целое число?
4. Пример целых чисел
5. Комплекты закрытые и целые
6. Объекты целого ряда

Натуральные числа — это числа, которые мы используем для счета.Они целые, неотрицательных чисел. Мы часто видим их представленными на числовой строке .

Линия на изображении выше начинается с 1 и увеличивается в значении до 5. Однако числа могут увеличиваться в значении бесконечно (обозначено пунктирной линией на изображении). Таким образом, натуральные числа могут продолжаться до бесконечности.

Набор натуральных чисел обычно обозначается символом ℕ . Например:

ℕ = {1, 2, 3, 4, 5, 6, 7…}

Набор натуральных чисел, включающий ноль, известен как целых чисел .Набор целых чисел обычно обозначается W . Например, это набор целых чисел:

Вт = {0, 1, 2, 3, 4, 5, 6, 7…}

Возможно, что сбивает с толку, некоторые авторы не включают ноль в набор целых чисел. В этом случае это то же самое, что и набор натуральных чисел.

Как упоминалось выше, натуральные числа должны быть целыми и положительными. Это имеет смысл по ряду причин, включая тот факт, что они считают числа.Допустим, учитель хочет подсчитать количество учеников в своем классе: она может сосчитать только всех детей.

Мы часто видим в статистике, опубликованной в Интернете, цифры, которые кажутся противоречащими «целостности» людей. Например, «средний размер семьи — 3,1 человека». Должно быть достаточно ясно, что невозможно иметь 0,1 человека, но это число является лишь средним. Среднее количество автомобилей на одно домохозяйство рассчитывается путем сложения общего количества автомобилей и деления на количество домохозяйств.После деления мы больше не работаем с натуральными числами. Скорее, у нас остается действительное число, в данном случае дробь.

Сумма или произведение натуральных чисел также являются натуральными числами. Например, 5 + 5 = 10 (все три из которых являются естественными) или 10 · 15 = 150.

Точно так же в физическом мире «натуральных» чисел нет смысла говорить, что у нас есть «что-то отрицательное». Скорее, мы говорим, что у нас есть ноль чего-то там, где его нет.Используя приведенный выше пример с учителем, если у учителя в настоящее время нет учеников в его классе, у него ноль учеников; В реальном мире нет смысла иметь отрицательных учеников.

Полный набор целых чисел равен набору из неотрицательных целых чисел. Целые числа похожи на целые числа, за исключением того, что они также могут быть отрицательными или нулевыми. Например: -10, -3, 0, 1 5.
Статья по теме: Целочисленные последовательности (CalculusHowTo.com).

Несколько примеров целых чисел: 3, 15, 998, 2, 232, 589.

Все следующие числа являются , а не целыми числами :

• Десятичные : 0,1, 5,23, 15,999, 1,7 ² .
• Фракции : ½, 1/27, 2 ½, 99/100.
• Отрицательные числа: -10, -99, -521.

В теории множеств целые числа подчиняются нескольким правилам. Набор целых чисел:
Замкнут на сложение и умножение. Возьмите два целых числа a и b. Если вы сложите затем (a + b = c), то «c» также будет целым числом.То же верно и для умножения: a · b = d.

Давайте рассмотрим несколько конкретных примеров с числами вместо переменных:

Набор целых чисел не закрывается для деления и вычитания. Если a — целое число, то существует еще одно целое число b, которое дает нецелочисленное решение. В обозначениях это:

Где «b», «c» и «d» не целые числа.

Примеры :

1. Вычитание:
   6 и 10 — целые числа,
   , но 7-9 = -2, что не является целым числом.
2. Раздел :
   4 и 5 — целые числа, но 4/5 — не целые числа.

• Целые числа являются коммутативными для сложения и умножения. Вы не можете вычесть два целых числа в любом порядке и получить тот же результат.
  В обозначениях: Для каждого a, b в наборе целых чисел a + b = b + a и a · b = b a.
  Пример : 10 — 1 не то же самое, что 1 — 10.
• Целые числа ассоциативны для сложения и умножения.Порядок добавления не важен (их можно сгруппировать в разном порядке).
  Для любых a, b и c в наборе целых чисел a (b · c) = (a · b) · c и (a + b) + c = a + (b + c).
• Набор целых чисел включает аддитивную идентичность (0). Ноль — это аддитивная идентичность целых чисел. В обозначениях a + 0 = a для каждого целого числа a.
• Мультипликативное тождество равно 1. Умножьте любое целое число на 1, и вы получите тот же результат. В обозначениях 1 · a = a.

Натуральное число: Каталожные номера

Расширение натуральных чисел до целых

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Что такое натуральные числа? Определение, примеры и факты

Натуральные числа являются частью системы счисления, включая все положительные целые числа от 1 до бесконечности. Натуральные числа также называются счетными числами, потому что они не включают ноль или отрицательные числа. Они являются частью действительных чисел, включая только положительные целые числа, но не ноль, дроби, десятичные дроби и отрицательные числа.

Введение в натуральные числа

Мы видим числа повсюду вокруг нас, для подсчета предметов, для обозначения или обмена денег, для измерения температуры, определения времени и т. Д.Эти числа, которые используются для подсчета объектов, называются « натуральных чисел ». Например, при подсчете предметов мы говорим 5 чашек, 6 книг, 1 бутылку и т. Д.

Что такое натуральные числа?

Натуральные числа относятся к набору всех целых чисел, за исключением 0. Эти числа широко используются в нашей повседневной деятельности и речи.

Определение натуральных чисел

Натуральные числа — это числа, которые используются для счета и являются частью действительных чисел.Набор натуральных чисел включает только положительные целые числа, то есть 1, 2, 3, 4, 5, 6, ……… .∞.

Примеры натуральных чисел

Натуральные числа, также известные как неотрицательные целые числа (все положительные целые числа). Некоторые примеры включают 23, 56, 78, 999, 100202 и так далее.

Набор натуральных чисел

Набор — это набор элементов (в данном контексте чисел). Набор натуральных чисел в математике записывается как {1,2,3, …}. Набор натуральных чисел обозначается символом N.N = {1,2,3,4,5, … ∞}

Форма ведомости	N = Набор всех номеров, начиная с 1.
Форма для обжарки	N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………}
Set Builder Form	N = {x: x — целое число, начиная с 1}

Наименьшее натуральное число

Наименьшее натуральное число — 1. Мы знаем, что наименьший элемент в N равен 1 и что для каждого элемента в N мы можем говорить о следующем элементе в терминах 1 и N (что на 1 больше, чем этот элемент).Например, два — на один больше, чем на один, три — на один, больше, чем на два, и так далее.

Натуральные числа от 1 до 100

натуральных чисел от 1 до 100 — это 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20. , 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 , 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70 , 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95 , 96, 97, 98, 99 и 100.

0 — натуральное число?

Нет, 0 НЕ является натуральным числом, потому что натуральные числа считаются числами. Для подсчета любого количества предметов мы начинаем отсчет с 1, а не с 0.

Натуральные числа нечетные

Нечетные натуральные числа — это нечетные числа, принадлежащие множеству N. Таким образом, набор нечетных натуральных чисел равен {1,3,5,7, …}.

Четные натуральные числа

Четные натуральные числа — это четные, точно делимые на 2 числа, принадлежащие множеству N.Таким образом, набор четных натуральных чисел равен {2,4,6,8, …}.

Натуральные числа и целые числа

Набор целых чисел такой же, как набор натуральных чисел, за исключением того, что он включает дополнительное число, равное 0. Набор целых чисел в математике записывается как {0,1,2,3, …} . Обозначается буквой W.

.

Вт = {0,1,2,3,4…}

Из приведенных выше определений мы можем понять, что каждое натуральное число — это целое число.Кроме того, каждое целое число, кроме 0, является натуральным числом. Можно сказать, что множество натуральных чисел — это подмножество множества целых чисел.

Разница между натуральными и целыми числами

Натуральные числа — это положительные числа, например 1, 2, 3, 4 и т. Д. Это числа, которые вы обычно считаете, и они продолжаются до бесконечности. Принимая во внимание, что все целые числа являются натуральными числами, включая 0, например, 0, 1, 2, 3, 4 и так далее.Целые числа включают в себя все целые числа и их отрицательные аналоги. например, -4, -3, -2, -1, 0,1, 2, 3, 4 и так далее. В следующей таблице показана разница между натуральным числом и целым числом.

Натуральное число	Целое число
Набор натуральных чисел равен N = {1,2,3, … ∞}	Набор целых чисел W = {0,1,2,3, …}
Наименьшее натуральное число — 1.	Наименьшее целое число — 0.
Все натуральные числа являются целыми числами, но все целые числа не являются натуральными числами.	Каждое целое число является натуральным числом, кроме нуля.

Натуральные числа в числовой прямой

Набор натуральных и целых чисел может отображаться в числовой строке, как показано ниже. Все положительные целые числа или целые числа в правой части 0 представляют натуральные числа, тогда как все положительные целые числа вместе с нулем представляют собой целые числа.

Свойства натуральных чисел

Четыре операции над натуральными числами: сложение, вычитание, умножение и деление — приводят к четырем основным свойствам натуральных чисел, как показано ниже:

• Закрытие собственности
• Ассоциативное свойство
• Коммутационная собственность
• Распределительная собственность

1. Закрытие собственности:

Сумма и произведение двух натуральных чисел всегда является натуральным числом.

• Замыкание свойства сложения: a + b = c ⇒ 1 + 2 = 3, 7 + 8 = 15. Это показывает, что сумма натуральных чисел всегда является натуральным числом.

• Замыкание. Свойство умножения: a × b = c ⇒ 2 × 3 = 6, 7 × 8 = 56 и т. Д. Это показывает, что произведение натуральных чисел всегда является натуральным числом.

Итак, набор натуральных чисел N замкнут при сложении и умножении, но не при вычитании и делении.

2. Ассоциативное свойство:

Сумма или произведение любых трех натуральных чисел остается неизменной, даже если группировка чисел изменилась.

• Ассоциативное свойство сложения: a + (b + c) = (a + b) + c ⇒ 2+ (3 + 1) = 2 + 4 = 6, и тот же результат получается в (2 + 3) + 1 = 5 + 1 = 6.

• Ассоциативное свойство умножения: a × (b × c) = (a × b) × c ⇒ 2 × (3 × 1) = 2 × 3 = 6 =, и тот же результат получается в (a × b) × c = (2 × 3) × 1 = 6 × 1 = 6.

Итак, набор натуральных чисел N ассоциативен при сложении и умножении, но этого не происходит в случае вычитания и деления.

3. Коммутативная собственность:

Сумма или произведение двух натуральных чисел остается неизменной даже после изменения порядка чисел.Коммутативное свойство N утверждает, что: Для всех a, b∈N: a + b = b + a и a × b = b × a.

• Коммутативное свойство сложения: a + b = b + a ⇒ 8 + 9 = 17 и b + a = 9 + 8 = 17.
• Коммутативное свойство умножения: a × b = b × a ⇒ 8 × 9 = 72 и 9 × 8 = 72.

Итак, набор натуральных чисел N коммутативен при сложении и умножении, но не при вычитании и делении.
Сведем эти три свойства натуральных чисел в таблицу.Итак, набор натуральных чисел N коммутативен относительно сложения и умножения.

Эксплуатация	Закрытие собственности	Ассоциативное свойство	Коммутативная собственность
Дополнение	да	да	да
Вычитание	№	№	№
Умножение	да	да	да
Отдел	№	№	№

4.Распределительная собственность:

• Дистрибутивное свойство умножения над сложением: a × (b + c) = a × b + a × c
• Дистрибутивное свойство умножения над вычитанием: a × (b − c) = a × b − a × c

Чтобы узнать больше о свойствах натуральных чисел, щелкните здесь.

Важные моменты

• 0 не натуральное число, это целое число.
• Отрицательные числа, дроби и десятичные дроби не являются ни натуральными, ни целыми числами.
• N замкнуто, ассоциативно и коммутативно как при сложении, так и при умножении (но не при вычитании и делении).

☛ Статьи по теме

Ознакомьтесь с еще несколькими интересными статьями, посвященными натуральным числам и свойствам.

Часто задаваемые вопросы о натуральных числах

Что такое натуральные числа в математике?

Натуральные числа — это числа, начинающиеся с 1 и заканчивающиеся бесконечностью.Другими словами, мы рассматривали натуральные числа как набор целых чисел, исключая число 0.

Каковы четыре основных свойства натуральных чисел в математике?

Четыре основных свойства натуральных чисел в математике:

1. Закрытие собственности
2. Ассоциативная собственность
3. Коммутативная собственность
4. Распределительная собственность

Число 0 — натуральное число?

Нет, 0 не натуральное число.Натуральные числа начинаются с 1 и могут быть указаны как 1, 2, 3, 4, 5 и т. Д.

Что такое пример натурального числа?

Натуральные числа могут быть указаны как 1, 2, 3, 4, 5 и т. Д. Итак, одним примером может быть 5.

23 натуральное число?

Да, 23 — натуральное число, потому что это положительное число, которое используется при счете.

Почему натуральные числа называются натуральными?

Натуральные числа называются натуральными, потому что они используются для естественного счета.Набор натуральных чисел — это самая основная система чисел, потому что она интуитивно понятна или естественна, отсюда и название. Мы используем натуральные числа в повседневной жизни, считая дискретные объекты, то есть объекты, которые можно подсчитать.

Каковы первые пять натуральных чисел?

Натуральные числа — это числа, которые используются для счета и являются частью действительных чисел. Первые пять натуральных чисел — это 1, 2, 3, 4 и 5.

Как найти сумму n натуральных чисел?

Чтобы найти сумму n натуральных чисел, мы используем формулу: Sum = n (n + 1) / 2, где n представляет количество членов.Например, если мы хотим найти сумму первых шести натуральных чисел: 1, 2, 3, 4, 5, 6, мы заменим n на 6 (общее количество членов) и решим формулу. Сумма = n (n + 1) / 2. 6 (6 + 1) / 2 = 42/2 = 21. Получаем 21 в качестве ответа.

Почему все натуральные числа целые?

Целые числа — это числа, которые образуют набор отрицательных и положительных чисел, включая ноль, а положительные числа относятся к категории натуральных чисел. Таким образом, все натуральные числа — целые.

свойств натуральных чисел — определения, примеры и часто задаваемые вопросы.

Свойства натуральных чисел относятся к результату четырех основных арифметических операций с натуральными числами. Натуральные числа — это целые числа, за исключением нуля. Эти числа используются в нашей повседневной деятельности и в речи. Натуральные числа — это одна из классификаций действительных чисел, которые включают только положительные целые числа, то есть 1, 2, 3, 4,5,6, ………. исключая ноль, дроби, десятичные дроби и отрицательные числа.Помните, что набор натуральных чисел не включает отрицательные числа или ноль.

Из этой статьи вы подробно узнаете о свойствах натуральных чисел.

Каковы свойства натуральных чисел?

Натуральные числа — это числа, которые являются целыми положительными числами и включают числа от 1 до бесконечности (∞). Эти числа являются счетными и обычно используются для расчетов. Набор натуральных чисел в математике — это набор, начинающийся с 1, то есть {1,2,3 ,…}. Набор натуральных чисел обозначается символом N. Четыре свойства натуральных чисел следующие:

1. Закрытие собственности
2. Ассоциативное свойство
3. Коммутационная собственность
4. Распределительная собственность

Давайте рассмотрим их подробнее.

Закрытие собственности

Замыкание натуральных чисел утверждает, что сложение и умножение двух или более натуральных чисел всегда приводит к натуральному числу.Проверим все четыре арифметических действия и все a, b ∈ N.

• Сложение: 1 + 5 = 6, 7 + 4 = 11 и т. Д. Очевидно, что полученное число или сумма является натуральным числом. Таким образом, a + b ∈ N для всех a, b ∈ N.
• Умножение: 2 × 5 = 10, 6 × 4 = 24 и т. Д. Очевидно, что полученное число или произведение является натуральным числом. Таким образом, a × b ∈ N для всех a, b ∈ N.
• Вычитание: 8 — 5 = 3, 7 — 2 = -5 и т. Д. Очевидно, результат может быть натуральным числом, а может и не быть.Таким образом, a — b или b — a ∉ N для всех a, b ∈ N.
• Деление: 15 ÷ 5 = 3, 10 ÷ 3 = 3,33 и т. Д. Очевидно, что результирующее число может быть натуральным числом, а может и не быть. Таким образом, a ÷ b или b ÷ a ∉ N для всех a, b ∈ N.

Таким образом, мы можем заключить, что набор натуральных чисел всегда замкнут при сложении и умножении, но случай вычитания и деления не тот.

Ассоциативное свойство

Ассоциативное свойство натуральных чисел гласит, что сумма или произведение любых трех натуральных чисел остается неизменной, хотя группировка чисел изменяется.Давайте проверим все четыре арифметических действия и все a, b, c ∈ N.

• Дополнение: a + (b + c) = (a + b) + c. 3 + (15 + 1) = 19 и (3 + 15) + 1 = 19.
• Умножение: a × (b × c) = (a × b) × c. 3 × (15 × 1) = 45 и (3 × 15) × 1 = 45.
• Вычитание: a — (b — c) ≠ (a — b) — c. 2 — (15-1) = — 12 и (2-15) — 1 = — 14.
• Деление: a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c. 2 ÷ (3 ÷ 6) = 4 и (2 ÷ 3) ÷ 6 = 0.11.

Таким образом, мы можем заключить, что набор натуральных чисел ассоциативен при сложении и умножении, но при вычитании и делении дело обстоит иначе. Итак, ассоциативное свойство N формулируется следующим образом: для всех a, b, c ∈ N, a + (b + c) = (a + b) + c и a × (b × c) = (a × b ) × с

Коммутативная собственность

Коммутативное свойство натуральных чисел гласит, что сумма или произведение двух натуральных чисел остается неизменным даже после изменения порядка чисел.Проверим все четыре арифметических действия и все a, b ∈ N.

• Дополнение: a + b = b + a.
• Умножение: a × b = b × a
• Вычитание: a — b ≠ b — a
• Подразделение: a ÷ b ≠ b ÷ a

Таким образом, мы можем заключить, что набор натуральных чисел коммутативен при сложении и умножении, но при вычитании и делении дело обстоит иначе. Итак, коммутативность N выражается следующим образом: для всех a, b ∈ N, a + b = b + a и a × b = b × a

Эксплуатация	Закрытие собственности	Ассоциативное свойство	Коммутативная собственность
Дополнение	да	да	да
Вычитание	№	№	№
Умножение	да	да	да
Отдел	№	№	№

Распределительная собственность

Распределительное свойство натуральных чисел устанавливает любое выражение с тремя числами a, b и c, заданное в форме a (b + c), тогда оно разрешается как a × (b + c) = ab + ac или a (b — c) = ab — ca, что означает, что операнд a распределяется между двумя другими операндами, b и c.

• Умножение натуральных чисел всегда является распределительным по сравнению с сложением. а × (b + c) = ab + ac
• Умножение натуральных чисел также является распределительным по сравнению с вычитанием. a × (b — c) = ab — ac

Пример: 3 × (2 + 5) = 3 × 2 + 3 × 5

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

3 × (2 + 5) = 3 × 7 = 21

3 × 2 + 3 × 5 = 6 + 15 = 21

а × (б — в) = а × б — а × в

Пример: 3 × (2–5) = 3 × 2–3 × 5

3 × (2 −5) = 3 × (−3) = −9

3 × 2 — 3 × 5 = 6 — 15 = −9

Статьи по теме

Ознакомьтесь с этими интересными статьями, посвященными свойствам натуральных чисел, для более глубокого понимания.

Часто задаваемые вопросы о свойствах натуральных чисел

Каковы свойства натуральных чисел в математике?

Свойства натуральных чисел:

1. Закрытие собственности
2. Ассоциативная собственность
3. Коммутативная собственность
4. Распределительная собственность

Является ли набор натуральных чисел ассоциативным при делении?

Набор натуральных чисел НЕ ассоциативен при делении.Например, рассмотрим три натуральных числа 6,4 и 2. Тогда: (6 ÷ 4) ÷ 2 = 3 ÷ 2 = 1. 6 ÷ (4 ÷ 2) = 6 ÷ 2 = 3. Таким образом, (6 ÷ 4) ÷ 2 ≠ 6 ÷ (4 ÷ 2).

Что вы подразумеваете под коммутативным свойством сложения?

Согласно коммутативному свойству сложения, натуральные числа можно складывать в любом порядке, и их ответ останется таким же. Формула для этого свойства: a + b = b + a, которая верна для любых a, b ∈ N. Например, 1 + 2 или 2 + 1, оба дадут одинаковый ответ.

Что означает ассоциативное свойство сложения?

Ассоциативное свойство сложения — это свойство натуральных чисел, которое гласит, что сумма трех или более чисел не изменится даже при изменении группировки чисел.Соответствующее уравнение: a + (b + c) = (a + b) + c. Здесь под группировкой понимается расположение данных чисел в круглых скобках.

Какое уравнение демонстрирует коммутативное свойство сложения?

Уравнение, демонстрирующее коммутативность сложения, — это «a + b = b + a». Возьмем пример: 4 + 3 = 3 + 4. Здесь сумма в обеих частях уравнения одинакова, то есть 7.

Какое уравнение показывает распределительное свойство умножения?

Уравнение, которое показывает распределительное свойство умножения: «a (b + c) = a b + a c».Здесь термины в круглых скобках не могут быть упрощены из-за одной или нескольких переменных.

Что такое натуральные числа? — Определение и примеры — Видео и стенограмма урока

Дальнейшее обсуждение и примеры натуральных чисел

В следующих примерах учащиеся продемонстрируют свои знания о множестве натуральных чисел и покажут, как этот набор сравнивается с другими наборами чисел. Будут исследованы другие операции с натуральными числами, чтобы определить, является ли результат по-прежнему натуральным числом.После выполнения примеров учащиеся должны иметь твердое представление о том, что такое натуральные числа и чем они отличаются от других наборов чисел.

Примеры

1) Какие из следующих чисел являются натуральными? 3, 19, -9, 27,5, 1, -3. Откуда вы знаете?

2) Возведенное в квадрат натуральное число также является натуральным числом? Как насчет квадратного корня из натурального числа?

3) Целые числа, обозначаемые Z, представляют собой набор положительных или отрицательных целых чисел и нуля.Действительные числа, обозначаемые R, представляют собой набор положительных или отрицательных целых или десятичных чисел и нуля. Каждое натуральное число тоже целое? Каждое натуральное число также является действительным числом?

Решения

1) Числа 3, 19 и 1 — натуральные числа, потому что они являются целыми положительными числами. -9 и -3 не являются натуральными числами, потому что они отрицательны, а 27,5 не является натуральным числом, потому что это не целое число.

2) Натуральное число в квадрате — это натуральное число, умноженное само на себя.2 = 3 * 3 = 9 по-прежнему является натуральным числом. Квадратный корень из натурального числа может быть натуральным числом, но обычно это не так. Например, квадратный корень из 4 равен 2, что является натуральным числом, но квадратный корень из 5 составляет приблизительно 2,236, что не является натуральным числом, поскольку это не целое число. Не гарантируется, что квадратный корень из натурального числа является натуральным числом.

3) Поскольку набор целых чисел включает в себя положительные или отрицательные целые числа и ноль, а набор натуральных чисел представляет собой набор положительных целых чисел (и, возможно, ноль), натуральные числа удовлетворяют условиям, чтобы быть целым числом.Таким образом, каждое натуральное число также является целым числом, но не каждое целое число является натуральным числом. Точно так же, поскольку набор действительных чисел включает в себя положительные или отрицательные целые или десятичные числа и ноль, натуральное число удовлетворяет условиям, чтобы быть действительным числом. Таким образом, каждое натуральное число также является действительным числом, но не каждое действительное число является натуральным числом.

Обсуждение

На уроке мы узнали, что если вы сложите или умножите два натуральных числа, результатом будет натуральное число, и что это не работает для деления или вычитания.Означает ли это, что натуральное число, деленное на другое натуральное число, никогда не может быть натуральным числом? Всегда ли при вычитании натуральных чисел получается неестественное число?

Руководство к обсуждению

Цель обсуждения состоит в том, чтобы студенты пришли к выводу, что деление и вычитание натуральных чисел не гарантирует получение натурального числа, но есть примеры, когда результатом является натуральное число. Например, 10/5 = 2 по-прежнему является натуральным числом, но 5/10 = 0.5 нет. Точно так же 5-10 = -5 не является естественным, но 10-5 = 5 является естественным. Посмотрите, могут ли студенты придумать правило деления или вычитания натуральных чисел, для которого результат гарантированно будет естественным.

натуральных, целых, рациональных, иррациональных, действительных чисел и выше

Натуральные числа

натуральных (или , считая ) чисел — 1,2,3,4,5 и т. Д. много натуральных чисел. Множество натуральных чисел, {1,2,3,4,5 ,…}, иногда для краткости пишут N .

Целые числа — натуральные числа вместе с 0.

(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)

Сумма любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел натуральное число (4 × 2000 = 8000). Этот однако это неверно для вычитания и деления.

Целые числа

целых чисел — это набор действительных чисел, состоящий из натуральных чисел, их аддитивных обратных чисел и нуля.

{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}

Набор целых чисел иногда написано J или Z для краткости.

сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.

Рациональные числа

рациональных чисел те числа, которые можно выразить как отношение между два целых числа. Например, дроби 13 и −11118 являются рациональное число.Все числа входят в рациональные числа, поскольку любое целое число z можно записать как отношение z1.

Все десятичные дроби, которые заканчиваются, являются рациональными числами (с версии 8.27 можно записать как 827100.) Десятичные дроби которые после некоторой точки имеют повторяющийся узор, также являются рациональными: например,

0,0833333 …. = 112.

Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разница, произведение и частное также являются рациональным числом (пока мы не делим на 0).

Иррациональные числа

Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме он никогда не заканчивается и не повторяется. В древние греки обнаружили, что не все числа рациональны; там — это уравнения, которые нельзя решить с помощью отношений целых чисел.

Первое такое уравнение для изучения было 2 = x2. Какие само число раз равно 2?

2 является около 1,414, поскольку 1,4142 = 1,999396, что близко к 2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив десятичный).Квадратный корень из 2 — иррациональное число, то есть его десятичный эквивалент продолжается вечно, без повторяющегося образца:

2 = 1,41421356237309 …

Другой известный иррациональный числа золотое сечение , число с большим значение для биологии:

1 + 52 = 1,61803398874989 …

π (пи), отношение длины окружности к ее диаметру:

π = 3,14159265358979 …

и е, самое важное число в исчислении:

е = 2.71828182845904 …

Иррациональные числа можно далее разделить на алгебраических чисел, которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями какого-либо полиномиального уравнения. π и e оба трансцендентны.

The Реальные числа

Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке.Существует бесконечно много действительных чисел, так же как бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.

«Меньший», или счетных бесконечности целых чисел и rationals иногда называют ℵ0 (alef-naught), и бесчисленных бесконечности реалов называется ℵ1 (алеф-он).

Есть еще «большие» бесконечности, но для этого вам следует взять курс теории множеств!

The Комплексные числа

Комплексные числа — множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1.(нажмите здесь, чтобы подробнее о мнимых числах и операциях с комплексными числами).

Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.

Этот набор иногда бывает записывается как C для краткости. Набор комплексных чисел важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .

За пределами …

Есть и «большие» наборы чисел, используемых математиками.Кватернионы , открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя разные мнимые единицы!

натуральных чисел

натуральных чисел

Конечная математика

Роберт С. Уилсон

4. Натуральные числа

Определение 4.1 : Пустой набор является набор, не имеющий элементов.

Теорема 4.1 : An пустой набор — это подмножество любого набора.

Теорема 4.2 : Любое два пустых множества равны.

В результате теоремы 4.2 мы можем ссылаться на пустое множество. В наиболее часто используемым обозначением пустого множества является греческая буква

Axiom 4 : Пустое множество — это установленный. ¹

Теперь мы можем определить натуральные числа. Первое натуральное число 0.

Определение 4.2 : Число 0 — это пустой набор.

Определение 4.3 : Если n натуральное число, преемник n является натуральным числом и является набором

Любое натуральное число получается последовательным взятием последователей. начиная с 0.

Обозначение : Если n — натуральное число, мы будем обозначать преемник n по

п + 1.

Теорема 4.3: (Слабая Индукция) : Пусть P (n) — утверждение, зависящее от естественного номер n.Если

а) (привязка) P (0) верно,

и если

b) (индукция) всякий раз, когда P (k) истинно, то также и P (k +1)

, то P (n) истинно для всех натуральных чисел n.

Теорема 4.4 : A натуральное число — это набор.

Определение 4.4 : Если есть один к одному соответствие между элементами коллекции объектов и элементы натурального числа, то мы говорим, что коллекция конечный .

Все коллекции объектов, которые мы будем рассматривать, будут конечный. Когда мы говорим «набор», мы будем иметь в виду конечное множество.

Определение 4.5 : Пусть A — множество. Мы говорим что A имеет n элементов , если существует взаимно однозначное соответствие между A и натуральным числом n. В этом случае n называется количество элементов в A или количество элементов в A .

Обозначение : Количество элементов в наборе A будет обозначаться по

# (А)

Определение 4.6 : Если m и n натуральные числа определяют

м < п

если

Если m < n, но m и n не равны, мы будем писать m < п.

Теорема 4.5 : Пусть m и n — любые натуральные числа.

• м < м.
• м < n и n < м, тогда m = n.
• Если m < n и n < p, то m < p.

Теорема 4.6: ( Закон трихотомии для натуральных чисел) : Если m и n — два натуральных числа числа тогда либо

т <п m = n

или

п <т

Теорема 4.7: Пусть n — натуральное число. Если

, затем

Теорема 4.8 : Каждое ненулевое натуральное число n имеет наибольший элемент.

Определение 4.7 : Пусть n ненулевое натуральное число. Тогда самый большой элемент n называется предшественник п.

: Обозначим предшественника n через n — 1.

Теорема 4.9 : Пусть S — непустое множество из n элементов. Если

, затем

# (S — {s}) = n — 1.

Теорема 4.10: a) Если n — любое натуральное число,

(п + 1) — 1 = п

б) Если n — любое натуральное число, отличное от нуля,

(п — 1) + 1 = п

Теорема 4.11 : Любой конечный набор натуральных чисел — это набор.

Теорема 4.12 : Если n натуральное число и

, то существует натуральное число m такое, что

# (S) = м. *

5. Подсчет

17.Натуральные числа и индукция — логика и доказательство 3.18.4 документация

Эта глава знаменует собой переход от абстрактного к конкретному. Рассмотрение математической вселенной в терминах множеств, отношений и функций дает нам полезные способы размышления о математических объектах и ​​структурах и отношениях между ними. Однако в какой-то момент нам нужно начать думать о конкретных математических объектах и ​​структурах, и натуральные числа — хорошее место для начала.Математик девятнадцатого века Леопольд Кронекер однажды провозгласил: «Бог создал целые числа; все остальное — дело рук человека ». Под этим он имел в виду, что натуральные числа (и целые числа, которые мы также обсудим ниже) являются фундаментальным компонентом математической вселенной, и что многие другие объекты и структуры, представляющие интерес, могут быть построены из них.

В этой главе мы рассмотрим натуральные числа и основные принципы, которые ими управляют. В главе 18 мы увидим, что даже базовые операции, такие как сложение и умножение, могут быть определены с помощью описанных здесь средств, а их свойства вытекают из этих основных принципов.Однако наша презентация в этой главе останется неформальной. В главе 19 мы увидим, как эти принципы проявляются в теории чисел, одной из старейших и наиболее почтенных областей математики.

17,1. Принцип индукции

Набор натуральных чисел — это набор

\ [\ mathbb {N} = \ {0, 1, 2, 3, \ ldots \}. \]

В прошлом мнения расходились относительно того, должен ли набор натуральных чисел начинаться с 0 или 1, но в наши дни большинство математиков принимают их за начало с 0.Логики часто называют функцию \ (s (n) = n + 1 \) функцией-преемником , поскольку она отображает каждое натуральное число \ (n \) на следующее за ним. Что делает натуральные числа особенными, так это то, что они сгенерированы числом ноль и функцией-преемником, то есть единственный способ построить натуральное число — это начать с \ (0 \) и применить функцию-преемник до конечного числа. много раз. С фундаментальной точки зрения, здесь существует опасность зайти в круг, потому что неясно, как мы можем объяснить, что значит применить функцию «конечное число раз», не говоря о самих натуральных числах.Но следующий принцип, известный как принцип индукции , описывает это существенное свойство натуральных чисел некруглым образом.

---

Принцип индукции. Пусть \ (P \) — любое свойство натуральных чисел. Предположим, что \ (P \) имеет нуль, и всякий раз, когда \ (P \) имеет натуральное число \ (n \), то оно имеет своего преемника \ (n + 1 \). Тогда \ (P \) выполняется для любого натурального числа.

---

Это отражает образ натуральных чисел, порождаемых нулем и операцией преемника: покрывая случаи нуля и преемника, мы заботимся обо всех натуральных числах.

Принцип индукции дает рецепт для доказательства того, что каждое натуральное число обладает определенным свойством: показать, что \ (P \) выполняется для любого натурального числа, показать, что оно верно для \ (0 \), и показать, что всякий раз, когда оно выполняется некоторого числа \ (n \), то имеет место \ (n + 1 \). Эта форма доказательства называется доказательством по индукции . Первая требуемая задача называется базовым случаем , а вторая требуемая задача называется вводным этапом . Шаг индукции требует временной фиксации натурального числа \ (n \), предполагая, что \ (P \) выполняется для \ (n \), а затем показать, что \ (P \) выполняется для \ (n + 1 \).В этом контексте предположение, что \ (P \) выполняется для \ (n \), называется индуктивной гипотезой .

Доказательство по индукции можно представить себе как метод одновременного сбивания бесконечного потока домино. Устанавливаем механизм на место и сбиваем домино 0 (базовый случай), и каждое домино сбивает следующее домино (шаг индукции). Таким образом, домино 0 сбивает домино 1; сбивает домино 2 и так далее.

Вот пример доказательства по индукции.{n + 2} — 1. \ end {split} \]

---

В обозначениях логики первого порядка, если мы напишем \ (P (n) \), чтобы обозначить, что \ (P \) выполняется для \ (n \), мы могли бы выразить принцип индукции следующим образом:

\ [P (0) \ клин \ forall n \; (P (n) \ to P (n + 1)) \ to \ forall n \; P (n). \]

Но обратите внимание, что принцип индукции гласит, что аксиома имеет значение для каждого свойства \ (P \), что означает, что мы должны правильно использовать универсальный квантор и для этого:

\ [\ forall P \; (P (0) \ клин \ forall n \; (P (n) \ to P (n + 1)) \ to \ forall n \; P (n)).\]

Количественная оценка свойств выводит нас из области логики первого порядка; поэтому индукция — это принцип второго порядка.

Образец доказательства по индукции еще более естественно выражается следующим естественным правилом дедукции:

Вам следует подумать о том, как некоторые доказательства в этой главе могут быть представлены формально с использованием естественной дедукции.

В качестве другого примера доказательства по индукции выведем формулу, которая для любого конечного множества \ (S \) определяет количество подмножеств \ (S \).n \) подмножества \ (S \).

Доказательство. Воспользуемся индукцией по \ (n \). В базовом случае есть только один набор с элементами \ (0 \), пустой набор, и есть ровно одно подмножество пустого набора, как требуется.

В индуктивном случае предположим, что \ (S \) имеет \ (n + 1 \) элементов. Пусть \ (a \) будет любым элементом \ (S \), и пусть \ (S ‘\) будет множеством, содержащим оставшиеся \ (n \) элементы. Чтобы подсчитать подмножества \ (S \), мы разделим их на две группы.

Сначала рассмотрим подмножества \ (S \), не содержащие \ (a \).{n + 1} \) подмножеств \ (S \), если требуется.

---

Мы видели, что существует соответствие между свойствами домена и подмножествами домена. Для каждого свойства \ (P \) натуральных чисел мы можем рассмотреть набор \ (S \) натуральных чисел с этим свойством, а для каждого набора натуральных чисел мы можем рассмотреть свойство нахождения в этом наборе. Например, мы можем говорить о свойстве быть четным или говорить о множестве четных чисел. При таком соответствии принцип индукции можно представить следующим образом:

---

Принцип индукции. Пусть \ (S \) — любой набор натуральных чисел, содержащий \ (0 \) и замкнутый относительно операции преемника. Тогда \ (S = \ mathbb {N} \).

---

Здесь утверждение, что \ (S \) «закрыто относительно операции-преемника», означает, что всякий раз, когда число \ (n \) находится в \ (S \), то же самое и \ (n + 1 \).

17,2. Варианты индукции

В этом разделе мы рассмотрим варианты принципа индукции, которые часто бывают полезными. Важно понимать, что каждый из них может быть оправдан с помощью принципа индукции, изложенного в последнем разделе, поэтому их не нужно рассматривать как фундаментальные.

Первый из них не очень хорош: вместо того, чтобы начинать с \ (0 \), мы можем начать с любого натурального числа, \ (m \).

---

Принцип индукции от начальной точки. Пусть \ (P \) — любое свойство натуральных чисел, и пусть \ (m \) — любое натуральное число. Предположим, что \ (P \) имеет место для \ (m \), и всякий раз, когда \ (P \) имеет натуральное число \ (n \), большее или равное \ (m \), то оно верно и для его преемника \ (п + 1 \). Тогда \ (P \) выполняется для любого натурального числа, большего или равного \ (m \).{n + 1}. \ end {split} \]

---

В качестве другого примера давайте выведем формулу для суммы углов в выпуклом многоугольнике. Многоугольник называется выпуклым , если каждая линия между двумя вершинами остается внутри многоугольника. Мы примем без доказательства визуально очевидный факт, что любой выпуклый многоугольник с более чем тремя сторонами можно подразделить на треугольник и выпуклый многоугольник с одной стороной меньше, а именно, закрывая любые две последовательные стороны, чтобы образовать треугольник. Мы также примем без доказательства основной геометрический факт, что сумма углов любого треугольника равна 180 градусам.

---

Теорема. Для любого \ (n \ geq 3 \) сумма углов любого выпуклого \ (n \) — угольника равна \ (180 (n — 2) \).

Доказательство. В базовом случае, когда \ (n = 3 \), это сводится к утверждению, что сумма углов в любом треугольнике равна 180 градусам.

Для шага индукции предположим, что \ (n \ geq 3 \), и пусть \ (P \) — выпуклый \ ((n + 1) \) — угольник. Разделите \ (P \) на треугольник и \ (n \) — угольник. По предположениям индукции сумма углов \ (n \) — угольника составляет \ (180 (n-2) \) градусов, а сумма углов треугольника равна \ (180 \) градусам.Меры этих углов вместе составляют сумму углов \ (P \), в сумме \ (180 (n-2) + 180 = 180 (n-1) \) градусов.

---

Для нашего второго примера мы рассмотрим принцип полной индукции , также иногда известной как полная индукция .

---

Принцип полной индукции. Пусть \ (P \) будет любым свойством, которое удовлетворяет следующему: для любого натурального числа \ (n \), всякий раз, когда \ (P \) выполняется для каждого числа, меньшего, чем \ (n \), оно также выполняется для \ (n \).Тогда \ (P \) выполняется для любого натурального числа.

---

Обратите внимание, что нет необходимости выделять особый случай для нуля: для любого свойства \ (P \), \ (P \) выполняется для всех натуральных чисел меньше нуля по той тривиальной причине, что нет любой! Так, в частности, любое такое свойство автоматически имеет нулевое значение.

Заметьте также, что если такое свойство \ (P \) выполняется для каждого числа, меньшего, чем \ (n \), то оно также выполняется для каждого числа, меньшего, чем \ (n + 1 \) (почему?). Итак, для такого \ (P \) из обычного принципа индукции следует, что для любого натурального числа \ (n \), \ (P \) выполняется для любого натурального числа, меньшего, чем \ (n \).Но это всего лишь окольный способ сказать, что \ (P \) выполняется для любого натурального числа. Другими словами, мы обосновали принцип полной индукции с помощью обычной индукции.

Чтобы использовать принцип полной индукции, мы просто должны позволить \ (n \) быть любым натуральным числом и показать, что \ (P \) выполняется для \ (n \), предполагая, что это верно для каждого меньшего числа. Сравните это с обычным принципом индукции, который требует от нас показать \ (P (n + 1) \), предполагая только \ (P (n) \). Следующий пример использования этого принципа дословно взят из введения к этой книге:

---

Теорема. Каждое натуральное число, большее или равное 2, может быть записано как произведение простых чисел.

Доказательство. Продолжаем индукцией по \ (n \). Пусть \ (n \) будет любым натуральным числом больше 2. Если \ (n \) простое число, мы закончили; мы можем рассматривать саму \ (n \) как продукт с одним множителем. В противном случае \ (n \) составно, и мы можем написать \ (n = m \ cdot k \), где \ (m \) и \ (k \) меньше \ (n \) и больше 1. По Согласно индуктивной гипотезе каждое из \ (m \) и \ (k \) может быть записано как произведение простых чисел:

\ [\ begin {split} m = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \\ k = q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v.\ end {split} \]

Но тогда у нас

\ [п = m \ cdot k = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \ cdot q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v. \]

Мы видим, что \ (n \) — произведение простых чисел, что и требовалось.

---

Наконец, мы рассмотрим другую формулировку индукции, известную как принцип наименьшего элемента.

---

Принцип наименьшего элемента. Предположим, что \ (P \) — некоторое свойство натуральных чисел, и предположим, что \ (P \) выполняется для некоторого \ (n \).Тогда существует наименьшее значение \ (n \), для которого выполняется \ (P \).

---

Фактически, используя классические рассуждения, это эквивалентно принципу полной индукции. Чтобы убедиться в этом, рассмотрим противоположность приведенного выше утверждения: «если не существует наименьшего значения, для которого выполняется \ (P \), то \ (P \) не имеет никакого натурального числа». Пусть \ (Q (n) \) будет свойством «\ (P \) не имеет , а не \ (n \)». Утверждение, что не существует наименьшего значения, для которого выполняется \ (P \), означает, что для каждого \ (n \), если \ (P \) выполняется в \ (n \), то оно имеет некоторое число, меньшее, чем \ ( п \); и это эквивалентно утверждению, что для каждого \ (n \), если \ (Q \) не выполняется в \ (n \), то существует меньшее значение, для которого \ (Q \) не выполняется .И , что эквивалентно утверждению, что если \ (Q \) выполняется для каждого числа, меньшего, чем \ (n \), то это верно и для \ (n \). Точно так же утверждение, что \ (P \) не выполняется ни для какого натурального числа, равносильно утверждению, что \ (Q \) выполняется для любого натурального числа. Другими словами, заменив принцип наименьшего элемента на его противоположный и заменив \ (P \) на «not \ (Q \)», мы получим принцип полной индукции. Поскольку каждое утверждение эквивалентно своему противоположному, и каждый предикат имеет свою отрицательную версию, эти два принципа одинаковы.

Поэтому неудивительно, что принцип наименьшего элемента можно использовать почти так же, как принцип полной индукции. Вот, например, формулировка предыдущего доказательства в этих терминах. Обратите внимание, что это сформулировано как доказательство от противоречия.

---

Теорема. Каждое натуральное число, большее 2, может быть записано как произведение простых чисел.

Доказательство. Предположим противное, что некоторое натуральное число, большее или равное 2, не может быть записано как произведение простых чисел.По принципу наименьшего элемента есть наименьший такой элемент; назовите это \ (n \). Тогда \ (n \) не является простым числом, и, поскольку оно больше или равно 2, оно должно быть составным. Следовательно, мы можем записать \ (n = m \ cdot k \), где \ (m \) и \ (k \) меньше \ (n \) и больше 1. По предположению о \ (n \) каждый \ (m \) и \ (k \) можно записать как произведение простых чисел:

\ [\ begin {split} m = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \\ k = q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v. \ end {split} \]

Но тогда у нас

\ [п = m \ cdot k = p_1 \ cdot p_2 \ cdot \ ldots \ cdot p_u \ cdot q_1 \ cdot q_2 \ cdot \ ldots \ cdot q_v.\]

Мы видим, что \ (n \) является произведением простых чисел, что противоречит тому факту, что \ (n \) не может быть написано как произведение простых чисел. n \).

Что более интересно, так это то, что два вышеуказанных условия определяют все значения \ (f \), то есть есть ровно одна функция, удовлетворяющая приведенной выше спецификации. Фактически, не имеет значения, что \ (f \) принимает значения в натуральных числах; он может принимать значения в любом другом домене. Все, что нужно, — это значение \ (f (0) \) и способ вычислить значение \ (f (n + 1) \) в терминах \ (n \) и \ (f (n) \ ). Вот что утверждает принцип определения с помощью рекурсии:

---

Принцип определения посредством рекурсии .Пусть \ (A \) — любое множество, и предположим, что \ (a \) находится в \ (A \), и \ (g: \ mathbb {N} \ times A \ to A \). Тогда существует единственная функция \ (f \), удовлетворяющая следующим двум пунктам:

\ [\ begin {split} f (0) & = a \\ f (n + 1) & = g (n, f (n)). \ end {split} \]

---

Принцип рекурсивного определения предъявляет сразу два утверждения: во-первых, что существует функция \ (f \), удовлетворяющая приведенным выше предложениям, и, во-вторых, что любые две функции \ (f_1 \) и \ (f_2 \) удовлетворяют эти предложения равны, то есть они имеют одинаковые значения для всех входных данных.В примере, с которого мы начали этот раздел, \ (A \) — это просто \ (\ mathbb {N} \) и \ (g (n, f (n)) = 2 \ cdot f (n) \).

В некоторых аксиоматических рамках принцип рекурсивного определения может быть оправдан с помощью принципа индукции. В других случаях принцип индукции можно рассматривать как частный случай принципа рекурсивного определения. А пока мы будем просто считать, что оба они являются фундаментальными свойствами натуральных чисел.

В качестве другого примера рекурсивного определения рассмотрим функцию \ (g: \ mathbb {N} \ to \ mathbb {N} \), рекурсивно определяемую следующими пунктами:

\ [\ begin {split} g (0) & = 1 \\ g (n + 1) & = (n + 1) \ cdot g (n) \ end {split} \]

Попробуйте вычислить первые несколько значений.Развернув определение, мы видим, что \ (g (n) = 1 \ cdot 2 \ cdot 3 \ cdot \ ldots \ cdot (n-1) \ cdot n \) для каждого \ (n \); действительно, определение с помощью рекурсии обычно является правильным способом сделать выражения с использованием «…» точными. Значение \ (g (n) \) читается как «\ (n \) факториал» и записывается \ (n! \).

Действительно, обозначение суммирования

\ [\ sum_ {i

и обозначение продукта

\ [\ prod_ {i

также можно сделать точным с помощью рекурсивных определений.Например, функция \ (k (n) = \ sum_ {i

\ [\ begin {split} k (0) & = 0 \\ k (n + 1) & = k (n) + f (n) \ end {split} \]

Индукция и рекурсия — взаимодополняющие принципы, и обычно способ доказать что-то о рекурсивно определенной функции — это использовать принцип индукции. Например, следующая теорема дает формулы для суммы \ (1 + 2 + \ ldots + n \) в терминах \ (n \).

---

Теорема.2 + 3n + 2} {2} \\ & = \ frac {(n + 1) (n + 2)} {2}. \ end {split} \]

---

Существует столько же вариаций принципа рекурсивного определения, сколько и вариаций принципа индукции. Например, по аналогии с принципом полной индукции, мы можем указать значение \ (f (n) \) в терминах значений, которые \ (f \) принимает на всех входах, меньших, чем \ (n \). Когда, например, \ (n \ geq 2 \), следующее определение определяет значение функции \ (\ mathrm {fib} (n) \) в терминах двух ее предшественников:

\ [\ begin {split} \ mathrm {fib} (0) & = 0 \\ \ mathrm {fib} (1) & = 1 \\ \ mathrm {fib} (n + 2) & = \ mathrm {fib} (n + 1) + \ mathrm {fib} (n) \ end {split} \]

Вычисляя значения \ (\ mathrm {fib} \) на \ (0, 1, 2, \ ldots \), получаем

\ [0, 1, 1, 2, 3, 5, 8, 13, 21, \ ldots \]

Здесь после второго числа каждое последующее число представляет собой сумму двух предшествующих ему значений.Это известно как последовательность Фибоначчи , а соответствующие числа известны как числа Фибоначчи . В обычном математическом представлении вместо \ (\ mathrm {fib} (n) \) записывается \ (F_n \), а последовательность определяется следующими уравнениями:

\ [F_0 = 0, \ quad F_1 = 1, \ quad F_ {n + 2} = F_ {n + 1} + F_n \]

Но теперь вы можете распознать такую ​​спецификацию как неявное обращение к принципу определения посредством рекурсии. Мы просим вас доказать некоторые факты о последовательности Фибоначчи в приведенных ниже упражнениях.

17,4. Определение арифметических операций

Фактически, мы можем даже использовать принцип рекурсивного определения, чтобы определить самые основные операции с натуральными числами и показать, что они обладают свойствами, которые мы ожидаем от них. С фундаментальной точки зрения, мы можем охарактеризовать натуральные числа как набор \ (\ mathbb {N} \) с выделенным элементом \ (0 \) и функцией \ (\ mathrm {succ} (m) \) , который для каждого натурального числа \ (m \) возвращает его преемника . Они удовлетворяют следующему:

• \ (0 \ neq \ mathrm {succ} (m) \) для любого \ (m \) в \ (\ mathbb {N} \).

• Для каждого \ (m \) и \ (n \) в \ (\ mathbb {N} \), если \ (m \ neq n \), то \ (\ mathrm {succ} (m) \ neq \ mathrm {succ} (п) \). Другими словами, \ (\ mathrm {succ} \) — это инъективный .

• Если \ (A \) — любое подмножество \ (\ mathbb {N} \) со свойством, что \ (0 \) находится в \ (A \), и всякий раз, когда \ (n \) находится в \ (A \ ), то \ (\ mathrm {succ} (n) \) находится в \ (A \), тогда \ (A = \ mathbb {N} \).

Последний пункт можно переформулировать как принцип индукции:

Предположим, что \ (P (n) \) — любое свойство натуральных чисел, такое, что \ (P \) выполняется для \ (0 \), и для любого \ (n \) \ (P (n) \) влечет \ (P (\ mathrm {succ} (п)) \).Тогда каждое \ (P \) выполняется любого натурального числа.

Помните, что этот принцип можно использовать для обоснования принципа определения рекурсией:

Пусть \ (A \) — любое множество, \ (a \) — любой элемент из \ (A \), и пусть \ (g (n, m) \) — любая функция из \ (\ mathbb {N} \ раз A \) к \ (A \). Тогда существует единственная функция \ (f: \ mathbb {N} \ to A \), удовлетворяющая следующим двум пунктам:

Мы можем использовать принцип рекурсивного определения для определения сложения с помощью следующих двух предложений:

\ [\ begin {split} m + 0 & = m \\ m + \ mathrm {succ} (n) & = \ mathrm {succ} (m + n) \ end {split} \]

Обратите внимание, что мы фиксируем \ (m \) и рассматриваем это как функцию от \ (n \).Если мы напишем \ (1 = \ mathrm {succ} (0) \), \ (2 = \ mathrm {succ} (1) \) и т. Д., Легко доказать \ (n + 1 = \ mathrm {succ} (n) \) из определения сложения.

Мы можем перейти к определению умножения, используя следующие два предложения:

\ [\ begin {split} m \ cdot 0 & = 0 \\ m \ cdot \ mathrm {succ} (n) & = m \ cdot n + m \ end {split} \]

Мы также можем определить функцию-предшественницу с помощью

\ [\ begin {split} \ mathrm {pred} (0) & = 0 \\ \ mathrm {pred} (\ mathrm {succ} (n)) & = n \ end {split} \]

Мы можем определить усеченное вычитание на

\ [\ begin {split} m \ dot — 0 & = m \\ m \ dot — (\ mathrm {succ} (n)) & = \ mathrm {pred} (m \ dot — n) \ end {split} \]

С помощью этих определений и принципа индукции можно доказать все следующие тождества:

• \ (n \ neq 0 \) подразумевает \ (\ mathrm {succ} (\ mathrm {pred} (n)) = n \)

• \ (0 + n = n \)

• \ (\ mathrm {succ} (m) + n = \ mathrm {succ} (m + n) \)

• \ ((m + n) + k = m + (n + k) \)

• \ (т + п = п + т \)

• \ (m (n + k) = mn + mk \)

• \ (0 \ cdot n = 0 \)

• \ (1 \ cdot n = n \)

• \ ((mn) k = m (nk) \)

• \ (мн = нм \)

Первые пять мы проделаем здесь, а оставшиеся оставим в качестве упражнений.

---

Предложение. Для каждого натурального числа \ (n \), если \ (n \ neq 0 \), то \ (\ mathrm {succ} (\ mathrm {pred} (n)) = n \).

Доказательство. По индукции по \ (n \). Мы исключили случай, когда \ (n \) равно \ (0 \), поэтому нам нужно только показать, что утверждение верно для \ (\ mathrm {succ} (n) \). Но в этом случае у нас есть \ (\ mathrm {succ} (\ mathrm {pred} (\ mathrm {succ} (n)) = \ mathrm {succ} (n) \) по второму определяющему предложению функции-предшественника

Предложение. Для каждого \ (n \), \ (0 + n = n \).

Доказательство. По индукции по \ (n \). У нас есть \ (0 + 0 = 0 \) по первому определяющему предложению для сложения. И, предполагая \ (0 + n = n \), мы имеем \ (0 + \ mathrm {succ} (n) = \ mathrm {succ} (0 + n) = n \), используя второе определяющее предложение для сложения.

Предложение. Для каждых \ (m \) и \ (n \), \ (\ mathrm {succ} (m) + n = \ mathrm {succ} (m + n) \).

Доказательство. Зафиксируйте \ (m \) и используйте индукцию по \ (n \). Тогда \ (n = 0 \), мы имеем \ (\ mathrm {succ} (m) + 0 = \ mathrm {succ} (m) = \ mathrm {succ} (m + 0) \), используя первое определение пункт для дополнения.Предполагая, что утверждение верно для \ (n \), имеем

\ [\ begin {split} \ mathrm {succ} (m) + \ mathrm {succ} (n) & = \ mathrm {succ} (\ mathrm {succ} (m) + n) \\ & = \ mathrm {succ} (\ mathrm {succ} (m + n)) \\ & = \ mathrm {succ} (m + \ mathrm {succ} (n)) \ end {split} \]

, используя индуктивную гипотезу и второе определяющее предложение для сложения.

Предложение. Для любых \ (m \), \ (n \) и \ (k \), \ ((m + n) + k = m + (n + k) \).

Доказательство. По индукции по \ (k \).Случай, когда \ (k = 0 \), прост, и на шаге индукции имеем

\ [\ begin {split} (m + n) + \ mathrm {succ} (k) & = \ mathrm {succ} ((m + n) + k) \\ & = \ mathrm {succ} (m + (n + k)) \\ & = m + \ mathrm {succ} (n + k) \\ & = m + (n + \ mathrm {succ} (k))) \ end {split} \]

, используя индуктивную гипотезу и определение сложения.

Предложение. Для каждой пары натуральных чисел \ (m \) и \ (n \), \ (m + n = n + m \).

Доказательство. По индукции по \ (n \). Базовый случай легко получить, используя второе предложение выше. На индуктивном шаге имеем

\ [\ begin {split} m + \ mathrm {succ} (n) & = \ mathrm {succ} (m + n) \\ & = \ mathrm {succ} (п + т) \\ & = \ mathrm {succ} (n) + m \ end {split} \]

, используя третье предложение выше.

---

17,5. Арифметика с натуральными числами

Продолжая, как в предыдущем разделе, мы можем установить все основные свойства натуральных чисел, которые играют роль в повседневной математике.Суммируем основные из них:

\ [\ begin {split} m + n & = n + m \ quad \ text {(коммутативность сложения)} \\ m + (n + k) & = (m + n) + k \ quad \ text {(ассоциативность сложения)} \\ n + 0 & = n \ quad \ text {($ 0 $ — нейтральный элемент для сложения)} \\ n \ cdot m & = m \ cdot n \ quad \ text {(коммутативность умножения)} \\ m \ cdot (n \ cdot k) & = (m \ cdot n) \ cdot k \ quad \ text {(ассоциативность умножения)} \\ n \ cdot 1 & = n \ quad \ text {($ 1 $ — нейтральный элемент для умножения)} \\ n \ cdot (m + k) & = n \ cdot m + n \ cdot k \ quad \ text {(дистрибутивность)} \\ n \ cdot 0 & = 0 \ quad \ text {($ 0 $ — поглощающий элемент для умножения)} \ end {split} \]

В обычном математическом аргументе или вычислении они могут использоваться без явного обоснования.У нас также есть следующие объекты недвижимости:

Мы можем определить \ (m \ le n \), «\ (m \) меньше или равно \ (n \)», чтобы обозначить, что существует \ (k \) такое, что \ (m + k = п \). Если мы это сделаем, нетрудно показать, что отношение «меньше или равно» удовлетворяет всем следующим свойствам для каждого \ (n \), \ (m \) и \ (k \):

• \ (n \ le n \) ( рефлексивность )

• если \ (n \ le m \) и \ (m \ le k \), то \ (n \ le k \) ( транзитивность )

• если \ (n \ le m \) и \ (m \ le n \), то \ (n = m \) ( антисимметрия )

• для всех \ (n \) и \ (m \), либо \ (n \ le m \), либо \ (m \ le n \) истинно ( совокупность )

• если \ (n \ le m \), то \ (n + k \ le m + k \)

• если \ (n + k \ le m + k \), то \ (n \ le m \)

• если \ (n \ le m \), то \ (nk \ le mk \)

• если \ (m \ ge n \), то \ (m = n \) или \ (m \ ge n + 1 \)

• \ (0 \ le n \)

Помните из главы 13, что первые четыре элемента утверждают, что \ (\ le \) является линейным порядком.Обратите внимание: когда мы пишем \ (m \ ge n \), мы имеем в виду \ (n \ le m \).

Как обычно, мы можем определить \ (m

---

Предложение. Для каждого \ (m \), \ (m + 1 \ not \ le 0 \).

Доказательство. В противном случае мы имели бы \ ((m + 1) + k = (m + k) + 1 = 0 \) для некоторого \ (k \).

---

В частности, взяв \ (m = 0 \), мы имеем \ (1 \ not \ le 0 \).

---

Предложение. Мы имеем \ (m

Доказательство. Предположим, \ (m

В другом направлении предположим \ (m + 1 \ le n \). Тогда \ (m \ le n \). У нас также есть \ (m \ ne n \), так как если бы \ (m = n \), у нас было бы \ (m + 1 \ le m + 0 \) и, следовательно, \ (1 \ le 0 \); противоречие .

---

Аналогичным образом мы можем показать, что \ (m

• \ (n иррефлексивность )

• если \ (n транзитивность )

• для всех \ (n \) и \ (m \), либо \ (n трихотомия )

• если \ (n

• если \ (k> 0 \) и \ (n

• если \ (m> n \), то \ (m = n + 1 \) или \ (m> n + 1 \)

• для всех \ (n \), \ (n = 0 \) или \ (n> 0 \)

Первые три элемента означают, что \ (<\) является строгим линейным порядком, а указанные выше свойства означают, что \ (\ le \) является связанным линейным порядком в смысле, описанном в разделе 13.1.

---

Доказательство . Мы докажем некоторые из этих свойств, используя предыдущую характеризацию отношения «меньше чем».

Первое свойство простое: мы знаем \ (n \ le n + 1 \), и если бы у нас было \ (n + 1 \ le n \), мы должны были бы иметь \ (n = n + 1 \), противоречие. .

Для второго свойства предположим \ (n

Что касается третьего, мы знаем, что либо \ (n \ le m \), либо \ (m \ le n \).Если \ (m = n \), мы закончили, в противном случае мы имеем либо \ (n

Для четвертого, если \ (n + 1 \ le m \), мы имеем \ (n + 1 + k = (n + k) + 1 \ le m + k \), как требуется.

Для пятого предположим, что \ (k> 0 \), то есть \ (k \ ge 1 \). Если \ (n

Остальные доказательства оставляем читателю в качестве упражнения.

---

Вот некоторые дополнительные свойства \ (<\) и \ (\ le \):

• \ (n )

• \ (n + 1> n \)

• если \ (n

• если \ (n \ le m \) и \ (m

• если \ (m> n \), то \ (m \ ge n + 1 \)

• если \ (m \ ge n \), то \ (m + 1> n \)

• если \ (n + k

• если \ (nk 0 \) и \ (n

Это подтверждается приведенным выше.Более того, набор принципов, которые мы только что рассмотрели, можно использовать для обоснования основных фактов о натуральных числах, которые снова обычно принимаются как должное в неформальных математических аргументах.

---

Предложение. Если \ (m \) и \ (n \) — натуральные числа такие, что \ (m + n = 0 \), то \ (m = n = 0 \).

Доказательство. Если \ (m + n = 0 \), то \ (m \ le 0 \), поэтому \ (m = 0 \) и \ (n = 0 + n = m + n = 0 \).

Предложение. Если \ (n \) — натуральное число такое, что \ (n <3 \), то \ (n = 0 \), \ (n = 1 \) или \ (n = 2 \).

Доказательство. В этом доказательстве мы неоднократно используем то свойство, что если \ (m> n \), то \ (m = n + 1 \) или \ (m> n + 1 \). Поскольку \ (2 + 1 = 3> n \), заключаем, что либо \ (2 + 1 = n + 1 \), либо \ (2 + 1> n + 1 \). В первом случае заключаем \ (n = 2 \), и все готово. Во втором случае заключаем \ (2> n \), из которого следует, что либо \ (2 = n + 1 \), либо \ (2> n + 1 \). В первом случае заключаем \ (n = 1 \), и все готово. Во втором случае мы заключаем \ (1> n \) и в последний раз обращаемся к общему принципу, представленному выше, чтобы заключить, что либо \ (1 = n + 1 \), либо \ (1> n + 1 \).В первом случае заключаем \ (n = 0 \), и все снова готово. Во втором случае заключаем, что \ (0> n \). Это приводит к противоречию, поскольку теперь \ (0> n \ ge 0 \), следовательно, \ (0> 0 \), что противоречит иррефлексивности \ (> \).

---

17,6. Целые числа

Натуральные числа предназначены для подсчета дискретных величин, но у них есть досадный недостаток: можно вычесть \ (n \) из \ (m \), если \ (n \) меньше или равно \ (m \ ), но не если \ (m \) больше, чем \ (n \).Набор из целых чисел , \ (\ mathbb {Z} \) дополняет натуральные числа отрицательными значениями, чтобы можно было выполнять вычитание полностью:

\ [\ mathbb {Z} = \ {\ ldots, -3, -2, -1, 0, 1, 2, 3, \ ldots \}. \]

В следующей главе мы увидим, что целые числа могут быть расширены до рациональных чисел , действительных чисел и комплексных чисел , каждое из которых служит полезным целям. Однако при работе с дискретными величинами целые числа уведут нас довольно далеко.

Целые числа можно представить как состоящие из двух копий натуральных чисел, положительной и отрицательной, с общим нулем. И наоборот, когда у нас есть целые числа, вы можете думать о натуральных числах как о состоящих из неотрицательных целых чисел, то есть целых чисел, которые больше или равны \ (0 \). Большинство математиков стирают различие между ними, хотя мы увидим, что в Lean, например, натуральные числа и целые числа представляют два разных типа данных.

Большинство свойств натуральных чисел, перечисленных в последнем разделе, также относятся к целым числам, но не ко всем. Например, это уже не тот случай, когда \ (n + 1 \ neq 0 \) для каждого \ (n \), поскольку утверждение неверно для \ (n = -1 \). В другом примере это не тот случай, когда каждое целое число либо равно \ (0 \), либо больше, чем \ (0 \), поскольку это не соответствует отрицательным целым числам.

Ключевым свойством, которым обладают целые числа, которое отличает их от натуральных чисел, является то, что для каждого целого числа \ (n \) существует значение \ (- n \) со свойством \ (n + (-n) = 0 \).Значение \ (- n \) называется отрицанием \ (n \). Мы определяем вычитание \ (n — m \) как \ (n + (-m) \). Для любого целого числа \ (n \) мы также определяем абсолютное значение числа \ (n \), записанное \ (| n | \), как \ (n \), если \ (n \ geq 0 \), и \ (- n \) в противном случае.

Мы больше не можем использовать доказательство индукцией по целым числам, потому что индукция не распространяется на отрицательные числа. Но мы можем использовать индукцию, чтобы показать, например, что свойство имеет место для каждого неотрицательного целого числа. Более того, мы знаем, что каждое отрицательное целое число является отрицанием положительного.2 \) как \ (F_ {n + 2} (F_ {n + 1} + F_n) \).

Докажите \ (\ sum_ {i

Подтвердите следующие две личности:

Совет: используйте индукцию по \ (n \) и докажите оба сразу. На шаге индукции раскройте \ (F_ {2n + 3} = F_ {2n + 2} + F_ {2n + 1} \) и аналогично для \ (F_ {2n + 4} \). Особенно сложно доказать второе уравнение. Используйте индуктивную гипотезу и первое тождество, чтобы упростить левую часть, и многократно разверните число Фибоначчи с наивысшим индексом и упростите уравнение, которое вам нужно доказать.0 \) считается степенью 2.

Пусть \ (V \) будет непустым набором целых чисел такой, что выполняются следующие два свойства:

• Если \ (x, y \ in V \), то \ (x — y \ in V \).

• Если \ (x \ in V \), то каждое кратное \ (x \) является элементом \ (V \).

Докажите, что существует некоторый \ (d \ in V \), такой, что \ (V \) равно множеству кратных \ (d \). Подсказка: используйте принцип наименьшего количества элементов.

Дайте неформальное, но подробное доказательство того, что для любого натурального числа \ (n \), \ (1 \ cdot n = n \), используя доказательство по индукции, определение умножения и теоремы, доказанные в разделе 17.4.

Покажите, что умножение распределяется по сложению. Другими словами, докажите, что для натуральных чисел \ (m \), \ (n \) и \ (k \), \ (m (n + k) = m n + m k \). Вам следует использовать определения сложения и умножения, а также факты, доказанные в Разделе 17.4 (но не более того).

Таким же образом докажите, что умножение ассоциативно. Вы можете использовать любой из фактов, доказанных в Разделе 17.4 и предыдущем упражнении.

Докажите, что умножение коммутативно.{nk} \).

Следуя примеру из Раздела 17.5, докажите, что если \ (n \) — натуральное число и \ (n <5 \), то \ (n \) - одно из значений \ (0, 1, 2, 3 \) или \ (4 \).

Докажите, что если \ (n \) и \ (m \) — натуральные числа и \ (n m = 1 \), то \ (n = m = 1 \), используя только свойства, перечисленные в Разделе 17.5.

Это сложно. Сначала покажите, что \ (n \) и \ (m \) больше \ (0 \) и, следовательно, больше или равны \ (1 \). Затем покажите, что если один из них больше, чем \ (1 \), то \ (n m> 1 \).

Докажите любые другие утверждения в Разделе 17.5, которые были заявлены без доказательств.

Докажите следующие свойства отрицания и вычитания для целых чисел, используя только свойства отрицания и вычитания, указанные в Разделе 17.6.

• Если \ (n + m = 0 \), то \ (m = -n \).

• \ (- 0 = 0 \).

• Если \ (- n = -m \), то \ (n = m \).

• \ (т + (п — т) = п \).

• \ (- (n + m) = -n — m \).

• Если \ (m 0 \).

• Если \ (m -n \).

• \ (п \ cdot (-m) = -nm \).

• \ (п (m — k) = нм — nk \).

• Если \ (n

Предположим, у вас есть бесконечная шахматная доска с натуральными числами, написанными в каждой клетке. Значение в каждом квадрате — это среднее значение четырех соседних квадратов.