Зависимость вязкости от давления и температуры
Содержание:
Зависимость вязкости от давления и температуры
- Многие экспериментально измеренные значения динамической вязкости чистых газов и жидкостей найдены во многих опубликованных источниках. Тем более что он полностью представлен. Рис. 1-3. Различные значения разгерметизации PPR = P / Pcr-снижение кинематической вязкости по отношению к зависящей от температуры cpr = p / / 1cr[15, 16. Справочник «Ландольт-Бернштейн» физико-химические таблицы. Если экспериментальные результаты отсутствуют и соответствующие измерения не могут быть выполнены, мы можем оценить значения динамической вязкости с использованием эмпирических методов, принимая во внимание другие данные, характеризующие material.
To облегчают такую оценку и показывают основные тенденции
динамической вязкости, связанные с температурой и давлением, 2 такие
методы корреляции описаны ниже. Обычная жидкая ния.
Дайсслер распространил свой анализ на эффекты на входе потока в трубу, а также и на другие потоки, включая и те, которые находятся вблизи критического состояния. Людмила Фирмаль
Показаны пониженные значения TPR = T / Tgr и пониженного давления ppr = p / pkr в зависимости от динамической вязкости ppr = p / pKr>с равной вязкостью при заданной температуре и давлении, деленные на соответствующие значения в критической точке. Из рисунка видно, что если давление стремится к нулю при заданной температуре, то динамическая вязкость газа стремится к определенному пределу(пределу пониженной динамической вязкости газа низкой плотности).Для большинства газов достижение этого предела является, по существу, уже давлением в 1 атм.
Динамическая вязкость газа низкой плотности увеличивается с увеличением температуры, а динамическая вязкость жидкости уменьшается с увеличением температуры. Экспериментальные значения RKR редко доступны. Однако значение / lcr может быть оценено с помощью одного из следующих 2 методов:1)если известны значения вязкости конкретных rpr и rpr, предпочтительно как можно ближе к конкретным rpr и rpr, то ccr — это QRP = / / [1Pr> 2)если исследователь имеет только данные p-V-T в критических точках, то значение ccr может быть оценено в виде: (1.13） Укр К; RKR представлен Μp.
- Значения кинематической вязкости в критической точке, рассчитанные по первому методу, суммируются в таблице (181.И приложение в-1 (стр. 675). Рис. 1-4 график значения= c / p°. он соответствует кинематической вязкости при определенной температуре и давлении и относится к кинематической вязкости при той же температуре, что и атмосферное давление. Приведенные значения отображаются на графике как функция перепада температуры и перепада давления.
Исходя из важных параметров, pn и Tpr могут быть вычислены и, исходя из этих значений, определены из диаграммы c / p-после чего стандарт должен быть умножен на значения, найденные таким образом *Для предварительного знакомства с теорией, исследования[141. Вязкость, которая может быть определена экспериментально или рассчитана с использованием теории разреженных газов, описанной в разделе 1.4°C. обратите внимание на приведенную диаграмму. 1-3 и 1-4 достаточно согласуются друг с другом в диапазоне изменения РПР и ТПР, если они перекрываются. Рис. 1-4.Зависимость динамики разгерметизации[17) * * = p / pO различных значений разгерметизации и разгерметизации = Г / ТКР.
В этих вычислениях он полагал, что число Прандтля и удельная теплоемкость постоянны, а вязкость и теплопроводность изменяются пропорционально степени 0,68 абсолютной температуры. Людмила Фирмаль
Рисунок 1-3 может быть использован для аппроксимации значений вязкости плотной газовой смеси.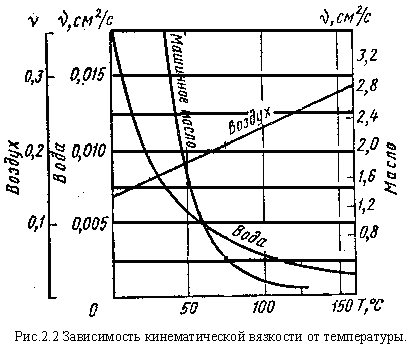
kr и Ikr, и в то же время используйте фигуру, как в случае чистой жидкости.
Этот метод недостаточно точен, когда в смеси присутствуют химически различные вещества или когда важные параметры компонентов смеси существенно различаются. [20] Приведенная выше схема расчета может быть применена к рисунку. 1-4.In в этом случае значение Р°смеси можно оценить по формуле (1.29).
Смотрите также:
Понятие динамической и кинетической вязкости
« НазадВязкостью называется свойство жидкости сопротивляться внешнему воздействию благодаря внутреннему трению, возникающему между слоями.
Для определения вязкости существует два основных параметра: динамическая вязкость и кинематическая вязкость, которые связаны между собой соотношением:
Где ν – кинематическая вязкость, м2/с;
µ — динамическая вязкость, Па*с;
ρ – плотность жидкости, кг/м3.
Между слоями жидкости, движущимися друг относительно друга, возникает сила.
Эта сила прямо пропорциональна скорости движения и площади соприкосновения.
В 1687 году И. Ньютоном был установлен закон вязкого течения жидкости:
где τ – касательные напряжения;
Коэффициент пропорциональности µ и назвали динамической вязкостью жидкости.
Динамическая и кинематическая вязкости зависят от температуры рабочей среды. Причем для газов и жидкостей эта зависимость различна. Это связано с различием во взаимодействии молекул. Для капельных жидкостей оба коэффициента убывают с возрастанием температуры.
Для определения вязкости используются специальные приборы – вискозиметры (U-образная стеклянная трубка). Одно из колен вискозиметра содержит впаянный капилляр, который оканчивается шариком. Под шариком и над ним нанесены метки, которые ограничивают определенный объем.
Для определения вязкости жидкости необходимо выбрать эталонную жидкость, вязкость которой является известной величиной. Для определения вязкости рабочей жидкости используется формула:
где µ — вязкость рабочей жидкости;
µ0 – вязкость эталонной жидкости;
t – время истечения через капилляр исследуемой жидкости;
t0 – время истечения через капилляр эталонной жидкости;
ρ – плотность исследуемой жидкости;
ρ0 – плотность эталонной жидкости.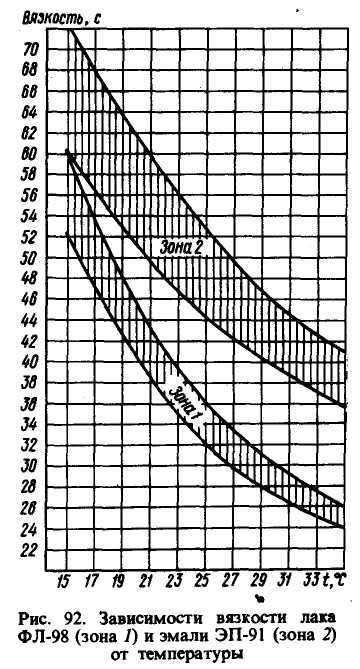
Так же существует понятие условной вязкости. Это отношение времени истечения через вискозиметр испытуемой жидкости при рабочей температуре к времени истечения дистиллированной воды при температуре 20°С (водное число). Водное соотношение является постоянной величиной для каждого прибора. Это соотношения выражается условными градусами.
где ВУ – условная вязкость;
tH2O – водное число.
Еще один метод определения вязкости жидкости – метод Стокса.
Он заключается в бросании различных шариков в жидкость и измерении скорости их падения. На шарик действуют три силы: сила тяжести, выталкивающая сила и сила сопротивления окружающей среды.
где Fтяж – сила тяжести;
m – масса шарика;
r – радиус шарика;
ρш – плотность шарика.
где FA– выталкивающая сила.
где Fc– сила сопротивления окружающей среды;
ϑ – скорость движения шарика.
Подставив выражения для сил, действующих на шарик в итоговое уравнение, можно найти вязкость жидкости:
где d – диаметр шарика;
t – время падения шарика;
l – расстояние, пройденной шариком.
« Назад
Вязкость жидкости
Вязкость жидкости – это свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке. Вязкость жидкости не может быть обнаружена при покое жидкости, так как она проявляется только при её движении. Для правильной оценки таких гидравлических сопротивлений, возникающих при движении жидкости, необходимо прежде всего установить законы внутреннего трения жидкости и составить ясное представление о механизме самого движения.
Содержание статьи
Физический смысл вязкости
Для понятия физической сущности такого понятия как вязкость жидкости рассмотрим пример.
Пусть есть две параллельные пластинки А и В. В пространство между ними заключена жидкость: нижняя пластинка неподвижна, а верхняя пластинка движется с некоторой постоянной скоростью υ1
Как при этом показывает опыт, слои жидкости, непосредственно прилегающие к пластинкам (так называемые прилипшие слои), будут иметь одинаковые с ним скорости, т.е. слой, прилегающий к нижней пластинке А, будет находиться в покое, а слой, примыкающий к верхней пластинке В, будет двигаться со скоростью υ1.
Промежуточные слои жидкости будут скользить друг по другу, причем их скорости будут пропорциональны расстояниям от нижней пластинки.
Ещё Ньютоном было высказано предположение, которое вскоре подтвердилось опытом, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Если взять площадь соприкосновения равной единице, это положение можно записать в виде
где τ – сила сопротивления, отнесенная к единице площади, или напряжение трения
μ – коэффициент пропорциональности, зависящий от рода жидкости и называемый коэффициентом абсолютной вязкости или просто абсолютной вязкостью жидкости.
Величину dυ/dy – изменение скорости в направлении, нормальном к направлению самой скорости, называют скоростью скольжения.
Таким образом вязкость жидкости – это физическое свойство жидкости, характеризующее их сопротивление скольжению или сдвигу
Вязкость кинематическая, динамическая и абсолютная
Теперь определимся с различными понятиям вязкости:
Динамическая вязкость. Единицей измерения этой вязкости является паскаль в секунду (Па*с). Физический смысл состоит в снижении давления в единицу времени. Динамическая вязкость характеризует сопротивление жидкости (или газа) смещению одного слоя относительно другого.
Динамическая вязкость зависит от температуры. Она уменьшается при повышении температуры и увеличивается при повышении давления.
Кинематическая вязкость. Единицей измерения является Стокс. Кинематическая вязкость получается как отношение динамической вязкости к плотности конкретного вещества.
Определение кинематической вязкости производится в классическом случае измерением времени вытекания определенного объема жидкости через калиброванное отверстие при воздействии силы тяжести
Абсолютная вязкость получается при умножении кинематической вязкости на плотность.
В международной системе единиц абсолютная вязкость измеряется в Н*с/м2 – эту единицу называют Пуазейлем.
Коэффициент вязкости жидкости
В гидравлике часто используют величину, получаемую в результате деления абсолютной вязкости на плотность. Эту величину называют коэффициентом кинематической вязкости жидкости или просто кинематической вязкостью и обозначают буквой ν. Таким образом кинематическая вязкость жидкости
ν = μ / ρ,
где ρ – плотность жидкости.
Единицей измерения кинематической вязкости жидкости в международной и технической системах единиц служит величина м2/с.
В физической системе единиц кинематическая вязкость имеет единицу измерения см2/с и называется Стоксом(Ст).
Вязкость некоторых жидкостей
| Жидкость | t, °С | ν, Ст |
| Вода | 0 | 0,0178 |
| Вода | 20 | 0,0101 |
| Вода | 100 | 0,0028 |
| Бензин | 18 | 0,0065 |
| Спирт винный | 18 | 0,0133 |
| Керосин | 18 | 0,0250 |
| Глицерин | 20 | 8,7 |
| Ртуть | 0 | 0,00125 |
Величину, обратную коэффициенту абсолютной вязкости жидкости, называют текучестью
ξ = 1/μ
Как показывают многочисленные эксперименты и наблюдения, вязкость жидкости уменьшается с увеличением температуры.
Для различных жидкостей зависимость вязкости от температуры получается различной.
Поэтому, при практических расчетах к выбору значения коэффициента вязкости следует подходить очень осторожно. В каждом отдельном случае целесообразно брать за основу специальные лабораторные исследования.
Вязкость жидкостей, как установлено из опытов, зависит так же и от давления. Вязкость возрастает при увеличении давления. Исключение в этом случае является вода, для которой при температуре до 32 градусов Цельсия с увеличением давления вязкость уменьшается.
Что касается газов, то зависимость вязкости от давления, так же как и от температуры, очень существенна. С увеличением давления кинематическая вязкость газов уменьшается, а с увеличением температуры, наоборот, увеличивается.
Методы измерения вязкости. Метод Стокса.
Область, посвященная измерению вязкости жидкости, называется вискозиметрия, а прибор для измерения вязкости называется вискозиметр.
Современные вискозиметры изготавливаются из прочных материалов, а при их производстве используются самые современные технологии, для обеспечение работы с высокой температурой и давлением без вреда для оборудования.
Существует следующие методы определения вязкости жидкости.
Капиллярный метод.
Сущность этого метода заключается в использовании сообщающихся сосудов. Два сосуда соединяются стеклянной трубкой известного диаметра и длины. Жидкость помещается в стеклянный канал и за определенный промежуток времени перетекает из одного сосуда в другой. Далее зная давление в первом сосуде и воспользовавшись для расчетов формулой Пуазейля определяется коэффициент вязкости.
Метод по Гессе.
Этот метод несколько сложнее предыдущего. Для его выполнения необходимо иметь две идентичные капиллярные установки. В первую помещают среду с заранее известным значением внутреннего трения, а во вторую – исследуемую жидкость. Затем замеряют время по первому методу на каждой из установок и составляя пропорцию между опытами находят интересующую вязкость.
Ротационный метод.
Для выполнения этого метода необходимо иметь конструкцию из двух цилиндров, причем один из них должен быть расположен внутри другого.
В промежуток между сосудами помещают исследуемую жидкость, а затем придают скорость внутреннему цилиндру.
Жидкость вращается вместе с цилиндром со своей угловой скоростью. Разница в силе момента цилиндра и жидкости позволяет определить вязкость последней.
Метод Стокса
Для выполнения этого опыта потребуется вискозиметр Гепплера, который представляет из себя цилиндр, заполненный жидкостью.
Вначале делаются две пометки по высоте цилиндра и замеряют расстояние между ними. Затем шарик определенного радиуса помещается в жидкость. Шарик начинает погружаться в жидкость и проходит расстояние от одной метки до другой. Это время фиксируется. Определив скорость движения шарика затем вычисляют вязкость жидкости.
Видео по теме вязкости
Определение вязкости играет большую роль в промышленности, поскольку определяет конструкцию оборудования для различных сред. Например, оборудование для добычи, переработки и транспортировки нефти.
Вместе со статьей «Вязкость жидкости» читают:
Плотность воздуха, его удельная теплоемкость, вязкость и другие физические свойства: таблицы при различных температурах
Рассмотрены основные физические свойства воздуха: плотность воздуха, его динамическая и кинематическая вязкость, удельная теплоемкость, теплопроводность, температуропроводность, число Прандтля и энтропия.
Свойства воздуха даны в таблицах в зависимости от температуры при нормальном атмосферном давлении.
Плотность воздуха в зависимости от температуры
Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа. Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.
На практике, чтобы узнать какова плотность воздуха при различных температурах, удобно воспользоваться готовыми таблицами. Например, приведенной таблицей значений плотности атмосферного воздуха в зависимости от его температуры.
Плотность воздуха в таблице выражена в килограммах на кубический метр и дана в интервале температуры от минус 50 до 1200 градусов Цельсия при нормальном атмосферном давлении (101325 Па).
| t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 |
|---|---|---|---|---|---|---|---|
| -50 | 1,584 | 20 | 1,205 | 150 | 0,835 | 600 | 0,404 |
| -45 | 1,549 | 30 | 1,165 | 160 | 0,815 | 650 | 0,383 |
| -40 | 1,515 | 40 | 1,128 | 170 | 0,797 | 700 | 0,362 |
| -35 | 1,484 | 50 | 1,093 | 180 | 0,779 | 750 | 0,346 |
| -30 | 1,453 | 60 | 1,06 | 190 | 0,763 | 800 | 0,329 |
| -25 | 1,424 | 70 | 1,029 | 200 | 0,746 | 850 | 0,315 |
| -20 | 1,395 | 80 | 1 | 250 | 0,674 | 900 | 0,301 |
| -15 | 1,369 | 90 | 0,972 | 300 | 0,615 | 950 | 0,289 |
| -10 | 1,342 | 100 | 0,946 | 350 | 0,566 | 1000 | 0,277 |
| -5 | 1,318 | 110 | 0,922 | 400 | 0,524 | 1050 | 0,267 |
| 0 | 1,293 | 120 | 0,898 | 450 | 0,49 | 1100 | 0,257 |
| 10 | 1,247 | 130 | 0,876 | 500 | 0,456 | 1150 | 0,248 |
| 15 | 1,226 | 140 | 0,854 | 550 | 0,43 | 1200 | 0,239 |
При 25°С воздух имеет плотность 1,185 кг/м3.
При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м3, что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение плотности газов при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.
Если сравнить плотность воздуха относительно плотности воды, то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м3, а плотность воздуха составляет 1,27 кг/м3. Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м3.
Динамическая и кинематическая вязкость воздуха при различных температурах
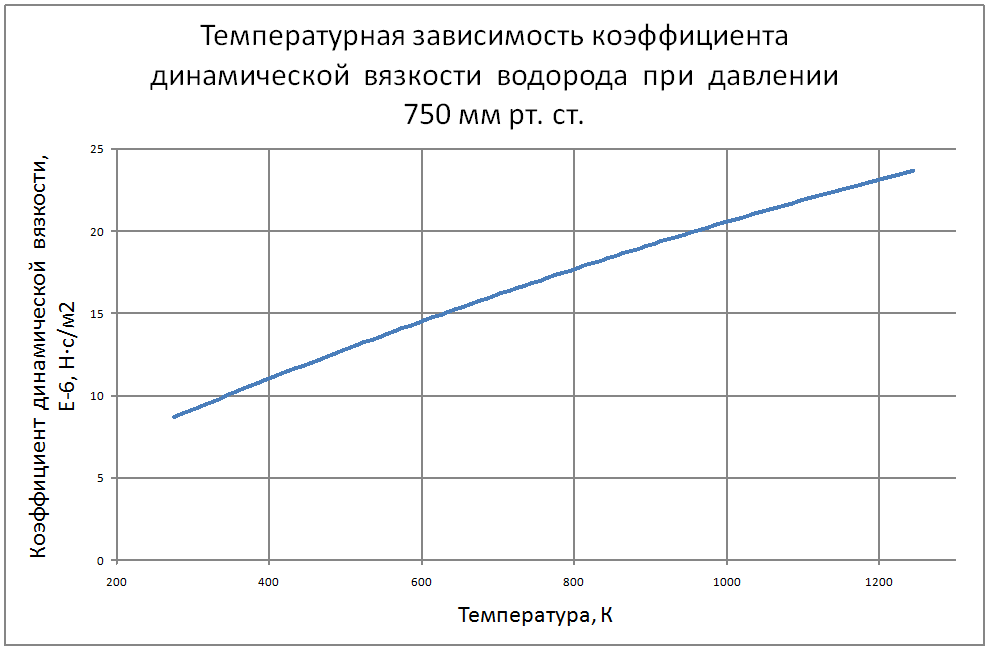
При выполнении тепловых расчетов необходимо знать значение вязкости воздуха (коэффициента вязкости) при различной температуре. Эта величина требуется для вычисления числа Рейнольдса, Грасгофа, Релея, значения которых определяют режим течения этого газа. В таблице даны значения коэффициентов динамической μ и кинематической ν вязкости воздуха в диапазоне температуры от -50 до 1200°С при атмосферном давлении.
Коэффициент вязкости воздуха с ростом его температуры значительно увеличивается. Например, кинематическая вязкость воздуха равна 15,06·10-6 м2/с при температуре 20°С, а с ростом температуры до 1200°С вязкость воздуха становиться равной 233,7·10-6 м2/с, то есть увеличивается в 15,5 раз! Динамическая вязкость воздуха при температуре 20°С равна 18,1·10-6 Па·с.
При нагревании воздуха увеличиваются значения как кинематической, так и динамической вязкости.
Эти две величины связаны между собой через величину плотности воздуха, значение которой уменьшается при нагревании этого газа. Увеличение кинематической и динамической вязкости воздуха (как и других газов) при нагреве связано с более интенсивным колебанием молекул воздуха вокруг их равновесного состояния (согласно МКТ).
| t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с |
|---|---|---|---|---|---|---|---|---|
| -50 | 14,6 | 9,23 | 70 | 20,6 | 20,02 | 350 | 31,4 | 55,46 |
| -45 | 14,9 | 9,64 | 80 | 21,1 | 21,09 | 400 | 33 | 63,09 |
| -40 | 15,2 | 10,04 | 90 | 21,5 | 22,1 | 450 | 34,6 | 69,28 |
| -35 | 15,5 | 10,42 | 100 | 21,9 | 23,13 | 500 | 36,2 | 79,38 |
| -30 | 15,7 | 10,8 | 110 | 22,4 | 24,3 | 550 | 37,7 | 88,14 |
| -25 | 16 | 11,21 | 120 | 22,8 | 25,45 | 600 | 39,1 | 96,89 |
| -20 | 16,2 | 11,61 | 130 | 23,3 | 26,63 | 650 | 40,5 | 106,15 |
| -15 | 16,5 | 12,02 | 140 | 23,7 | 27,8 | 700 | 41,8 | 115,4 |
| -10 | 16,7 | 12,43 | 150 | 24,1 | 28,95 | 750 | 43,1 | 125,1 |
| -5 | 17 | 12,86 | 160 | 24,5 | 30,09 | 800 | 44,3 | 134,8 |
| 0 | 17,2 | 13,28 | 170 | 24,9 | 31,29 | 850 | 45,5 | 145 |
| 10 | 17,6 | 14,16 | 180 | 25,3 | 32,49 | 900 | 46,7 | 155,1 |
| 15 | 17,9 | 14,61 | 190 | 25,7 | 33,67 | 950 | 47,9 | 166,1 |
| 20 | 18,1 | 15,06 | 200 | 26 | 34,85 | 1000 | 49 | 177,1 |
| 30 | 18,6 | 16 | 225 | 26,7 | 37,73 | 1050 | 50,1 | 188,2 |
| 40 | 19,1 | 16,96 | 250 | 27,4 | 40,61 | 1100 | 51,2 | 199,3 |
| 50 | 19,6 | 17,95 | 300 | 29,7 | 48,33 | 1150 | 52,4 | 216,5 |
| 60 | 20,1 | 18,97 | 325 | 30,6 | 51,9 | 1200 | 53,5 | 233,7 |
Примечание: Будьте внимательны! Вязкость воздуха дана в степени 106.
Удельная теплоемкость воздуха при температуре от -50 до 1200°С
Представлена таблица удельной теплоемкости воздуха при различных температурах. Теплоемкость в таблице дана при постоянном давлении (изобарная теплоемкость воздуха) в интервале температуры от минус 50 до 1200°С для воздуха в сухом состоянии. Чему равна удельная теплоемкость воздуха? Величина удельной теплоемкости определяет количество тепла, которое необходимо подвести к одному килограмму воздуха при постоянном давлении для увеличения его температуры на 1 градус. Например, при 20°С для нагревания 1 кг этого газа на 1°С в изобарном процессе, требуется подвести 1005 Дж тепла.
Удельная теплоемкость воздуха увеличивается с ростом его температуры. Однако, зависимость массовой теплоемкости воздуха от температуры не линейная. В интервале от -50 до 120°С ее величина практически не меняется — в этих условиях средняя теплоемкость воздуха равна 1010 Дж/(кг·град). По данным таблицы видно, что значительное влияние температура начинает оказывать со значения 130°С. Однако, температура воздуха влияет на его удельную теплоемкость намного слабее, чем на вязкость. Так, при нагреве с 0 до 1200°С теплоемкость воздуха увеличивается лишь в 1,2 раза – с 1005 до 1210 Дж/(кг·град).
Следует отметить, что теплоемкость влажного воздуха выше, чем сухого. Если сравнить теплоемкость воды и воздуха, то очевидно, что вода обладает более высоким ее значением и содержание воды в воздухе приводит к увеличению удельной теплоемкости.
| t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) |
|---|---|---|---|---|---|---|---|
| -50 | 1013 | 20 | 1005 | 150 | 1015 | 600 | 1114 |
| -45 | 1013 | 30 | 1005 | 160 | 1017 | 650 | 1125 |
| -40 | 1013 | 40 | 1005 | 170 | 1020 | 700 | 1135 |
| -35 | 1013 | 50 | 1005 | 180 | 1022 | 750 | 1146 |
| -30 | 1013 | 60 | 1005 | 190 | 1024 | 800 | 1156 |
| -25 | 1011 | 70 | 1009 | 200 | 1026 | 850 | 1164 |
| -20 | 1009 | 80 | 1009 | 250 | 1037 | 900 | 1172 |
| -15 | 1009 | 90 | 1009 | 300 | 1047 | 950 | 1179 |
| -10 | 1009 | 100 | 1009 | 350 | 1058 | 1000 | 1185 |
| -5 | 1007 | 110 | 1009 | 400 | 1068 | 1050 | 1191 |
| 0 | 1005 | 120 | 1009 | 450 | 1081 | 1100 | 1197 |
| 10 | 1005 | 130 | 1011 | 500 | 1093 | 1150 | 1204 |
| 15 | 1005 | 140 | 1013 | 550 | 1104 | 1200 | 1210 |
Теплопроводность, температуропроводность, число Прандтля воздуха
В таблице представлены такие физические свойства атмосферного воздуха, как теплопроводность, температуропроводность и его число Прандтля в зависимости от температуры. Теплофизические свойства воздуха даны в интервале от -50 до 1200°С для сухого воздуха. По данным таблицы видно, что указанные свойства воздуха существенно зависят от температуры и температурная зависимость рассмотренных свойств этого газа различна.
Теплопроводность воздуха λ при повышении температуры увеличивается во всем диапазоне, достигая при 1200°С величины 0,0915 Вт/(м·град). Другие теплофизические свойства воздуха такие, как его температуропроводность a и число Прандтля Pr, по-разному реагируют на изменение температуры. Температуропроводность, как и вязкость воздуха сильно зависит от температуры и при нагревании, например с 0 до 1200°С, ее значение увеличивается почти в 17 раз.
Число Прандтля воздуха слабо зависит от температуры и при нагревании этого газа его величина сначала снижается до величины 0,674, а затем начинает расти, и при температуре 1200°С достигает значения 0,724.
| t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr | t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr |
|---|---|---|---|---|---|---|---|
| -50 | 2,04 | 12,7 | 0,728 | 170 | 3,71 | 45,7 | 0,682 |
| -40 | 2,12 | 13,8 | 0,728 | 180 | 3,78 | 47,5 | 0,681 |
| -30 | 2,2 | 14,9 | 0,723 | 190 | 3,86 | 49,5 | 0,681 |
| -20 | 2,28 | 16,2 | 0,716 | 200 | 3,93 | 51,4 | 0,68 |
| -10 | 2,36 | 17,4 | 0,712 | 250 | 4,27 | 61 | 0,677 |
| 0 | 2,44 | 18,8 | 0,707 | 300 | 4,6 | 71,6 | 0,674 |
| 10 | 2,51 | 20 | 0,705 | 350 | 4,91 | 81,9 | 0,676 |
| 20 | 2,59 | 21,4 | 0,703 | 400 | 5,21 | 93,1 | 0,678 |
| 30 | 2,67 | 22,9 | 0,701 | 450 | 5,48 | 104,2 | 0,683 |
| 40 | 2,76 | 24,3 | 0,699 | 500 | 5,74 | 115,3 | 0,687 |
| 50 | 2,83 | 25,7 | 0,698 | 550 | 5,98 | 126,8 | 0,693 |
| 60 | 2,9 | 27,2 | 0,696 | 600 | 6,22 | 138,3 | 0,699 |
| 70 | 2,96 | 28,6 | 0,694 | 650 | 6,47 | 150,9 | 0,703 |
| 80 | 3,05 | 30,2 | 0,692 | 700 | 6,71 | 163,4 | 0,706 |
| 90 | 3,13 | 31,9 | 0,69 | 750 | 6,95 | 176,1 | 0,71 |
| 100 | 3,21 | 33,6 | 0,688 | 800 | 7,18 | 188,8 | 0,713 |
| 110 | 3,28 | 35,2 | 0,687 | 850 | 7,41 | 202,5 | 0,715 |
| 120 | 3,34 | 36,8 | 0,686 | 900 | 7,63 | 216,2 | 0,717 |
| 130 | 3,42 | 38,6 | 0,685 | 950 | 7,85 | 231,1 | 0,718 |
| 140 | 3,49 | 40,3 | 0,684 | 1000 | 8,07 | 245,9 | 0,719 |
| 150 | 3,57 | 42,1 | 0,683 | 1100 | 8,5 | 276,2 | 0,722 |
| 160 | 3,64 | 43,9 | 0,682 | 1200 | 9,15 | 316,5 | 0,724 |
Будьте внимательны! Теплопроводность воздуха в таблице указана в степени 102. Не забудьте разделить на 100! Температуропроводность воздуха указана в степени 106. Допускается интерполяция значений физических свойств воздуха в приведенных таблицах.
Энтропия сухого воздуха
В таблице представлены значения такого теплофизического свойства воздуха, как удельная энтропия. Значения энтропии даны для сухого воздуха в размерности кДж/(кг·град) в зависимости от температуры и давления. Удельная энтропия указана в таблице в интервале температуры от -50 до 50°С при давлении воздуха от 90 до 110 кПа. Следует отметить, что при нормальном атмосферном давлении (101,325 кПа) и температуре, например 30°С, удельная энтропия воздуха равна 0,1044 кДж/(кг·град).
Источники:
- Михеев М.А., Михеева И.М. Основы теплопередачи.
- Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная теника. Кондиционирование воздуха. Свойства веществ: Справ./ Под ред. С.Н. Богданова. 4-е изд., перераб. и доп. — СПб.: СПбГАХПТ, 1999.- 320 с.
Изменение Вязкость кинематическая — Энциклопедия по машиностроению XXL
Кривые изменения вязкости в зависимости от температуры для некоторых жидкостей изображены на рис. 73 и 74 кривая на рис. 73 дает значения кинематической вязкости машинного масла, а на [c.104]Отношение кинематической вязкости при t° к кинематической вязкости при tl — показатель, характеризующий степень изменения вязкости при данном температурном интервале, определяющий поведение масла в момент пуска механизма и при его установившемся режиме работы. [c.441]
Зависимость вязкости от температуры принято характеризовать отношением кинематической вязкости при / = 50 °С к кинематической вязкости при /=100°С. Чем меньше это отношение, тем выше вязкостно-температурные свойства масла. Степень изменения вязкости масла от температуры выражается также индексом вязкости (ИВ). Чем выще его значение, тем лучше масло. [c.40]
Существенный недостаток нефтяных масел — изменение вязкости в зависимости от температуры и давления с повыщением температуры и падением давления вязкость масел снижается. В литературе обычно приводят значение кинематической вязкости масла при 40 °С (V40), при 50 °С ( Vjq), при 100 °С (V[o o). [c.202]
На фиг. 16, а приведена кривая, характеризующая изменение кинематической вязкости при 38° С минерального масла под действием облучения нейтронами (в ядерном реакторе). На фиг. 16, б приведен график зависимости изменения вязкости турбинных масел различных начальных вязкостей при 38° С под действием разных доз ядерного облучения. [c.75]
Основным показателем качества масел является кинематическая вязкость, выражаемая в стоксах с размерностью см /с (1 Ст=100 сСт). Вязкостно-температурные свойства характеризуют изменения вязкости масла при изменении температуры и оцениваются индексом вязкости. Чем выше этот показатель, тем лучше вязкостно-температурные свойства масла, тем меньше изменяется его вязкость при изменении температуры, тем выше пусковые качества масла. Кроме того, качество масел оценивается содержанием водорастворимых кислот и щелочей, температурой вспышки, зольностью, коррозионной стойкостью и моющими свойствами. [c.123]
Для несжимаемых жидкостей коэффициент кинематической вязкости, вообще говоря, убывает с возрастанием тедшературы. В качестве иллюстрации здесь приведен график изменения коэффициента кинематической вязкости воды нри изменении температуры (фиг. 180). [c.443]
Таким образом, в вязкой жидкости циркуляция скорости по любому замкнутому контуру, а следовательно, и интенсивность вихрей, изменяется с течением времени, причем скорость этого изменения пропорциональна кинематическому коэффициенту вязкости жидкости. Скорость изменения циркуляции зависит, кроме того, от неравномерности распределения в пространстве составляющих (л. Чем более неравномерно распределены составляющие (О (т. е. чем больше величины производных по координатам от составляющих (1>), тем больше и, следовательно, тем быстрее происходит изменение [c.539]
Для относительной оценки вязкостно-температурны свойств различных масел с одинаковой кинематической-вязкостью используется индекс вязкости. Индекс вязкости выражают в условных единицах. При его определении сравнивают пологость кривой изменения вязкости в зависимости от температуры испытуемого масла с аналогичными кривыми двух эталонных масел, имеющих при температуре 98,8 °С ту же вязкость, что и испытуемое масло. Пологость кривых изменения вязкости масла оценивают при температуре 37,8 С. Эталонное масло с наименьшей зависимостью вязкости от температуры (пологая кривая) оценивается индексом вязкости в 100 единиц, с наибольшей зависимостью (крутая кривая) — в О единиц. Индекс вязкости определяют по специальным номограммам или таблицам. Масла с большим значени- [c.57]
При повышении температуры дымовых газов в печи-натуре до 1300° С изменение их кинематической вязкости и коэффициента температуропроводности показано сплошными линиями на рис. 51. [c.167]
Вязкостно-температурные свойства масел для двигателей характеризуют их способность, образовывать масляный слой, разделяющий металлические поверхности трущихся деталей, что обеспечивает уменьшение трения и износа. Вязкостно-температурные свойства моторных масел определяются кинематической вязкостью при 100, 50 и 0°С, температурой застывания, а также величиной индекса вязкости, характеризующего степень изменения вязкости масел в зависимости от температуры. Масла, применяемые в зимнее время и всесезонно, должны иметь высокий индекс вязкости, более низкую температуру застывания и меньшую вязкость при низких температурах, чем летние масла. [c.418]
На рис. 93 показано изменение коэфициента кинематической вязкости керосина в зависимости от температуры. Вязкость керосина резко увеличивается при температурах ниже 5, —10° С. [c.112]
Ошибки третьей группы возникают при эксплуатации механизмов. Они обусловлены местными искажениями профиля контактирующих поверхностей, изменением упругих деформаций, колебательными процессами и т. п., вызванными действующими силами (см. гл. 23, 24). К этой группе относятся и температурные ошибки, возникающие при изменении линейных размеров звеньев и механических свойств их материалов, а также вязкости смазывающих материалов при изменении температуры в механизме. Весьма существенны ошибки, связанные с изнашиванием элементов кинематических пар. [c.335]Численная оценка критериев подобия по типичным условиям работы машин и аппаратов, в которых эти явления наблюдаются, позволяет выявить основные характеристики экспериментального стенда. Например, диапазон изменения числа Прандтля определяет виды рабочих тел, которые должны быть использованы в эксперименте часто в экспериментальной установке используется то же рабочее тело, что и в натурных условиях. Пределы изменения числа Рейнольдса определяют диапазон изменения расхода рабочего тела, его давления и температуры (от давления и температуры зависят кинематический коэффициент вязкости и плотность, а от плотности и расхода — скорость рабочего тела). [c.21]
Если скорость потока уменьшить, то турбулентный режим вновь переходит в ламинарный. Скорость, при которой в данных условиях происходит изменение режимов движения, называется критической. Опытным путем было установлено, что величина прямо пропорциональна кинематической вязкости v и обратно пропорциональна диаметру трубы d, т. е. ш, р = kv/d. Безразмерный эмпирический коэффициент k, входящий в формулу, одинаков для всех жидкостей и газов и не зависит от диаметра трубы. Отсюда следует, что изменение режима движения происходит при определенном сочетании параметров d н v. Этот коэффициент называется критическим числом Рейнольдса [c.286]
Большие значения кинематической вязкости газов, а также отмеченные выше особенности ее изменения, на первый взгляд, могут показаться парадоксальными. Однако это легко объяснить, если учесть что в знаменатель выражения для кинематической вязкости (4.2) входит плотность, подверженная для газов очень большим изменениям в зависимости от температуры и давления и имеющая для них весьма малые, по сравнению с капельными жидкостями, значения. [c.105]
Составим выражение для потери напора на бесконечно малом участке трубопровода длиной dL, на котором изменением кинематической вязкости можно пренебречь, [c.250]
Изменение кинематического коэффициента вязкости у при изменении температуры для воды и смазочного масла, м /сек [c.17]
При давлениях, встречающихся в большинстве случаев на практике (до 2-10 Па = 200 ат), кинематическая вязкость капельных жидкостей весьма мало зависит от давления, и этим изменением в обычных гидравлических расчетах пренебрегают. Кинематическая вязкость газов зависит как от температуры, так и от давления, возрастая с увеличением температуры и уменьшаясь с увеличением давления (табл. 7). Кинематическая вязкость воздуха для нормальных условий (температура 20 °С, давление 1 10 Па = 1 ат) [c.18]
Применение нефтепромыслового оборудования в районах Западной Сибири и Севера налагает специальные требования к эксплуатации гидроприводов из-за значительного изменения характеристик рабочих жидкостей. При отрицательных температурах повыщаются коэффициенты кинематических вязкостей рабочих жидкостей, в связи с чем понижаются гидромеханический и объемный к. п. д. (особенно в период пуска) насосов и гидродвигателей повышаются потери в гидроцилиндрах (для рабочих жидкостей АМГ-10 и ВМГ-3 потери давления в системе возрастают в 3—4 раза при температуре —30°С и в 10—15 раз при температурах от —50°С до —60°С по сравнению с потерями при температурах -)-40°С + 50°С) увеличивается время стабилизации теплового режима гидросистемы. [c.141]
Условная вязкость — характеристика, получаемая при определенной методике испытания. Эта величина связывается с динамической и кинематической вязкостью приближенными эмпирическими соотношениями. Такие методы менее совершенны, чем описанные выше, но все еще находят широкое применение, правда, все более сокращающееся. Вязкость всех жидкостей, если только они при нагреве не претерпевают химических изменений, весьма сильно уменьшается с повышением температуры. Поэтому при определении вязкости необходимо знать точное значение заданной температуры испытуемой жидкости во время измерения. С этой целью, как правило, приборы снабжаются водяной баней или другим приспособлением для создания и поддержания требующейся температуры жидкости. [c.184]
В общей теории конвективного теплообмена доказывается, что толщины гидродинамического и теплового пограничных слоев точно совпадают только в среде, имеющей число Рг=, при течении без изменения давления и подобии граничных условий по скоростям течения и температурам. Во всех остальных случаях эти толщины не равны друг другу и их соотнощение зависит в первую очередь от соотнощения кинематической вязкости и температуропроводности среды, т.е. от чис-л а Рг. [c.163] Таким образом, число -псевдоожижения будет варьировать прямо пропорционально изменению кинематического коэффициента вязкости потока. Значит, в области высоких температур потока газо в число псевдоожижения будет выше. При псевдоожижении капельной жидкостью, наоборот, в области более высокой температуры потока число псевдоожижения будет ниже. [c.65]Вязкость рабочих жидкостей изменяется с давлением и, особенно сильно, с температурой. На рис. 4.1, а показана зависимость кинематического коэффициента вязкости некоторых распространенных масел от температуры. Изменение вязкости с температурой столь значительно, что для уменьшения масштаба по оси ординат откладывается величина Ig v. На рис. 4.1, б вязкость этих же масел отложена по оси ординат в масштабе Iglg v, а по оси абсцисс откладываются IgT = Ig (273 + °). В таком масштабе кривые вязкости практически спрямляются, поэтому для определения вязкости может применяться уравнение [c.100]
Вязкостно-температурные свойства характеризуют изменение вязкости масел при изменении температуры. С повышением температуры вязкость масел уменьшается и наоборот. Чем меньше изменяется вязкость масла при изменении температуры, тем лучше масло, тем лучше его пусковые качества. Показателями вязкостно-температурных свойств являются отношение кинематической вязкости при 50°С к вязкости при 100° С (чем этот показатель меньше, тем лучше вязкостно-температурные свойства) и индекс вязкости. Оценка по индексу вязкости основана на сравнении вязкостнотемпературных свойств испытуемого масла с вязкостно-температурными свойствами двух эталонных масел. Чем выше индекс вязкости, тем лучше вязко-стно-температурные свойства масла. [c.252]
Для большинства стабильных топлив с ростом давления кинематическая вязкость увеличивается, причем для разных температур эта зависимость может быть различной. Изменение вязкости сидкости в зависимости от давления характеризуется уравнением [c.287]
Боттерилл и Десаи [83], с одной стороны, изучали влияние давления на теплообмен псевдоожиженного слоя с поверхностью, а с другой — использовали его как фактор, изменяющий вязкость газа с целью выявления ее роли в механизме теплопереноса. Было найдено, что данные ряды экспериментов в атмосферах гелия, неона, воздуха и углекислого газа могут быть представлены в виде зависимости величины, обратной максимальному коэффициенту теплообмена, 1/ 1пах от комплекса (l/fe)X X (ц/р)[87]. Однако двукратного увеличения максимального коэффициента теплообмена, ожидаемого, в соответствии с приведенным соотношением, при изменении давления от атмосферного до 0,8 МПа в опытах [83] с плотным движущимся слоем не произошло При увеличении рабочего давления до 1 МПа во всех исследованных системах газ — твердые частицы коэффициенты возросли всего на 15%. Это позволило сделать вывод о том, что кинематическая вязкость не является главным фактором, который определяет интенсивность переноса тепла, и оказанное ею коррелирующее воздействие было случайно. В опытах с псевдоожиженным слоем наблюдалось существенное влияние изменения давления в аппарате на величину коэффициентов теплообмена с поверхностью при использовании в качестве сжижаемого материала крупных частиц узкого фракционного состава. Например, для псевдоожиженного воздухом слоя медной [c.69]
Как указывалось выше, толщина диффузионного слоя (которая колеблется обычно в пределах 0,001—0,1 см) растет при увеличении кинематической вязкости электролита v и коэффициента диффузии диффундирующего вещества и уменьшается при увеличении скорости движения электролита v . Коэффициент диффузии кислорода в воде равен 1,86 10″ см /с при 16° С и 1,875 10″ mV при 2, 7° С, т. е. увеличивается с ростом температуры. Изменение коэффициента диффузии кислорода в водных растворах Na l при 18° С приведено ниже [c.238]
У многих материалов (полимеры, бетон, металлы при повышенной температуре) в эксплуатационных условиях закон связи а(е) существенно зависит от времени. Изменение напряжений и деформаций во времени при постоянных внешних нагрузках называют ползучестью (явление ползучести можно обнаружить при растяжении материалов даже в условиях нормальной температуры). Так, при растяжении образца для снятия показаний тензометров приходится, как правило, приостанавливать процесс нагружения либо по силам, либо по деформациям. Такая остановка в упругой области практически не приводит к изменению показаний во времени. Если остановка происходит в пластической области, то для машин кинематического типа (e = onst) благодаря вязкости материала происходит заметное самопроизвольное падение напряжений (рис. 1.12), т. е. релаксация. При нормальной температуре Та напряжение а асимптотически стремится к [c.37]
В далыю илем будем рассматривать случаи, когда изменением тем1иературы воды можно пренебречь, и примем коэффициент кинематической вязкости в среднем для /=10″ С [c.121]
В третьей главе рассматриваются основные концепции теории осредненного турбулентного движения. В этой главе рассматривается зурбулентное движение в гидравлически гладких трубах, уточняется структура пристенного турбулентного движения, рассматривается изменение турбулентной вязкости от координат, составляется уравнение турбулентного движения, теоретически описываются кинематические и динамические параметры, дается сопоставление с известными экспериментами, раскрывается физическая сущность известных и вновь полученных функций (коэффициентов) связей, формулируется инвариантный закон сопротивления жидкости, дается инженерный метод расчета турбулентного движения в гидравлически гладких трубах и т.п. [c.7]
В предельном случае модельная структура пристенного турбулентного движения состоит из трех элементов 1) вязкой среды возле твердой поверхности 2) крупномасштабных образований (крупномасштабная турбулентность), отрываюшцхся от вязкой среды в результате волнового взаимодействия вязкой и турбулентных сред и 3) турбулентной среды в основном потоке, состоящей из мелкомасштабной турбулентности, зависящей от предыстории движения/33-56/. Крупномасштабная турбулентность, разрушаясь, поддерживает мелкомасштабную турбулентность. Мелкомасштабная турбулентность стремится к однородной турбулентности однако крупномасштабные вязкие струи поддерживают неоднородную турбулентность. Таким образом, пристенная турбулентность генерируется в результате волнового взаимодействия вязкой среды с турбулентной и только в результате такого взаимодействия поддерживается эта турбулентность. Если бы на время удалось приостановить приток крупных образований в турбулентную среду со стороны вязкого подслоя, то в ядре потока образовалось бы движение, аналогичное молекулярному движению разреженных газов, т.е. со скольжением относительно твердой поверхности при этом имелось бы постоянное значение турбулентной вязкости. По-видимому, такое явление имеет место, но периодического характера. Наличие крупных образований между вязкой и турбулентной средами сглаживает это скольжение и образуется плавное изменение поля скоростей. Однако влияние вязких струй на турбулентное ядро потока с удалением от стенки уменьшается и при определенных условиях в ядре потока имеет место однородная турбулентность. При обычных экспериментальных исследованиях кинематические параметры на границе вязкой и турбулентной сред осредняются в пространстве и во времени /33-56/. [c.51]
Гетерогенные смеси, их движения, последствия воздействия на них, возникающие в них волны чрезвычайно многообразны, что является следствием многообразия комбинаций фаз, их структур, многообразия межфазных и впутрифазных взаимодействий и процессов (вязкость и межфазное трение, теплопроводность и межфазный теплообмен, фазовые переходы и химические реакции, дробление и коагуляция капель и пузырей, различные сжимаемости фаз, прочность, капиллярные силы и т. д.) и многообразия различных видов воздействия на смеси. Например, в га-зовзвесях образуются размазанные волны, структура и затухание которых определяются главным образом силами межфазного трения с газом и дроблением капель или частиц. В жидкости с пузырьками газа или пара из-за радиальных пульсаций пузырьков, помимо размазанных волп, характерными являются волны с осцилляционной структурой, сильно зависящей от процессов тепло- и массообмена, а также дробления пузырьков. Далее в конденсированных средах фазовые переходы, инициируемые сильными ударными волнами, могут привести к многофронтовым волнам из-за немонотонного изменения сжимаемости среды при фазовых превращениях. Своеобразные волновые течения с кинематическими волнами возникают и при фильтрации многофазных жидкостей. [c.5]
Вязкость жидкостей меняется с изменением температуры с повышением температуры вязкость капельных жидкостей быстро уменьшается. Так, например, для воды кинематический коэффициент вязкости уменьшается от v= 1,78- л / e/ при t = 0° до V = 0,28 10 м /сск при t — 100° С, для смазочного масла — от V = 6,4 10 м 1сек при = 0° до v = 0,22 10 м 1сек при = 60° С и т. д. [c.17]
Изменение кинематической вязкости нефтепродуктов v от температуры t можно представить формулой П. А. Филонова v = v exp —н7), где Vq — кинематическая вязкость при i = 0″ С (или при температуре [c.10]
Интервал изменения числа Rei на объекте Re » модели среды с такой же кинематической вязкостью Vj = Vj, = 1 получаем следующее условие для максимальной скорости в модели = 10 щ . [c.339]
Поскольку известно, что существует однозначная связь между критериями Био, Нуссельта и Рейнольдса, предполагалось, что воспроизведение на газодинамических стендах закона изменения температуры газового потока по профилю лопатки Т = Гпов (О и мени в течение цикла, а также числа Рейнольдса Re = Непов (О приведет к однозначному воспроизведению неустановившихся тепловых и напряженных состояний. Поэтому была создана специальная испытательная камера, с помощью которой испытывалась только одна лопатка. На выходе устанавливалось регулируемое гидравлическое сопротивление, с помощью которого можно было создать любое заданное статическое давление, позволявшее получить в камере газ с плотностью и кинематической вязкостью, обеспечивающими получение реального значения чисел Re = Re (i). При этом в соответствии с выбранными реальными режимами эксплуатации воспроизводились графики изменения температуры и критерии Рейнольдса в течение всего цикла. Полученные экспериментально тепловые состояния считались основными при проведении исследований по изучению закономерностей разрушения. [c.196]
Экспресс-лаборатория позволяет определять физикохимические характеристики нефтепродуктов (плотность 1 одержание водорастворимых кислот и щелочей (ВРКЩ) кинематическую вязкость кислотное число масел содержание механических примесей и воды), следить за изменением качества масел в процессе их эксплуатации, проверять качество хранящихся нефтепродуктов. В лаборатории ЭЛАН не проводят анализов, связанных с определением температуры вспышки, поэтому ею можно пользоваться в помещениях, где нет особой вытяжк паров легких кефтепродуктов. [c.307]
Что такое кинематическая вязкость?
Кинематическая вязкость — это свойство жидкостей и газов, которое показывает, насколько легко данное вещество может течь. На практике это тесно связано с толщиной вещества. Абсолютная и кинематическая вязкость изменяются в зависимости от температуры.
Ученый со стаканамиЧтобы получить кинематическую вязкость, абсолютную вязкость вещества делят на его плотность.Кинематическая вязкость обозначается греческой буквой nu , которая напоминает букву «v»; абсолютная вязкость представлена как mu , что похоже на «u;» а плотность представлена цифрой rho , которая напоминает букву «p». Следовательно, уравнение v = u / p.
Абсолютная вязкость, также называемая динамической вязкостью, измеряет сопротивление вещества течению.Она определяется экспериментально путем помещения жидкости или газа между двумя пластинами и приложения известного количества давления для перемещения верхней пластины — динамическая вязкость зависит от давления, количества времени, в течение которого она была приложена, и расстояния, на которое пластина перемещалась в этом направлении. время. Динамическая или абсолютная вязкость основана на единицах паскаль-секунд (Па * с) Международной системы единиц (СИ), что означает, что если давление в 1 Па применяется в течение 1 секунды, пластина перемещается на то же расстояние, что и расстояние между двумя пластинами. 2 / с) в британской системе мер.2 / с.
Тепло влияет на свойства материала, поэтому оба типа вязкости изменяются при более высоких температурах. Когда жидкость нагревается, она течет легче, и поэтому вязкость уменьшается. На кинематическую вязкость влияет несколько меньше, чем на абсолютную вязкость, поскольку тепло также снижает плотность, поскольку молекулы расходятся дальше друг от друга при нагревании вещества.Вязкость газов увеличивается при более высоких температурах — по мере того, как газ расширяется, он оказывает большее давление на пластину, что затрудняет ее движение.
Температурная зависимость
Колебание μ в зависимости от температуры
Умеренная зависимость μ определяется двумя факторами; рассеяние фононов и рассеяние на ионизованных примесях.С повышением температуры тепловые колебания (фононы) внутри полупроводника увеличиваются и вызывают повышенное рассеяние. Это приводит к снижению подвижности носителей. Мы знаем, что
, где tau — среднее время свободного пробега между столкновениями. Среднюю длину свободного пробега можно записать как пропорциональную
Теперь рассмотрим, что длина свободного пробега обратно пропорциональна вероятности рассеяния, и что вероятность рассеяния можно считать пропорциональной энергии решетки (т.е.е. к Т). Это позволяет записать тау как
.Таким образом, мы ожидаем, что это снижение подвижности будет пропорционально T -3/2 .
Однако эффект рассеяния ионизованной примеси уменьшается с повышением температуры из-за более высоких средних тепловых скоростей носителей. Носители проводят меньше времени рядом с ионизированной примесью по мере прохождения, и, таким образом, уменьшается эффект рассеяния. Это моделируется, предполагая, что никакого рассеяния не произойдет, если электрон не окажется достаточно близко к иону, чтобы электростатическая энергия была сопоставима с тепловой энергией.
, что дает радиус
.
Далее, мы можем утверждать, что рассеивающая способность иона может быть представлена сечением рассеяния
.
Наконец, предполагая, что длина свободного пробега обратно пропорциональна сечению рассеяния, мы получаем соотношение
.
Следовательно, можно ожидать, что подвижность из-за рассеяния ионизованных примесей будет увеличиваться при повышении температуры в соответствии с T +3/2 .
Эти два эффекта действуют одновременно, при этом общее время столкновения равно
.Обычно рассеяние на ионизованных примесях преобладает при низких температурах, тогда как при более высоких температурах преобладает рассеяние на фононах. Экспериментальные значения температурной зависимости подвижности в Si, Ge и GaAs приведены в таблице ниже [1].
| Si | Ge | GaAs | |
Подвижность электронов | Т -2.4 | т -1,7 | т -1,0 |
| Отверстие Mobikity | Т -2,2 | т -2,3 | Т -2,1 |
Влияние температуры на V H
Чтобы понять, как напряжение Холла изменяется с температурой, мы должны сначала рассмотреть проводимость измеряемого образца. Электропроводность полупроводника можно выразить следующим образом:
Обратите внимание, что как концентрации носителей (N e и N h ), так и подвижности зависят от температуры, хотя и имеют разные функциональные формы.
В диапазоне примесных температур, где Т достаточно велика только для ионизации любых доноров в полупроводнике, концентрации носителей остаются постоянными, и единственное изменение сигма с температурой является результатом изменения подвижностей. Если предположить, что рассеяние фононов доминирует, мы знаем, что μ изменяется как T -3/2 . Таким образом, мы знаем σ ~ T -3/2 , и, учитывая, что σ = 1 / ρ и ρ∝R, мы можем определить, что R ~ T 3/2 .
Как указывалось ранее, напряжение Холла можно записать как
, где только ток зависит от температуры.Этот ток I можно записать в виде
, что означает, что I и, следовательно, V H изменяются в соответствии с T 3/2 . На самом деле эти колебания температуры довольно малы, и V H на практике можно считать постоянным во внешнем режиме.
В собственной области, в которой температура достаточно высока для возбуждения носителей заряда из валентной зоны в зону проводимости, концентрации носителей (N e и N h ) экспоненциально возрастают с ростом T.Это доминирует над любым воздействием подвижности на электрическую проводимость и приводит к быстрому уменьшению удельного сопротивления полупроводника с повышением температуры. Таким образом, напряжение Холла падает с увеличением T.
Определение энергетического разрыва
Изменение проводимости с температурой также позволяет нам измерить энергетический зазор между валентной зоной и зоной проводимости. И снова проводимость полупроводника
.Что касается внутреннего материала, мы знаем, что
Объединение этих двух уравнений дает
Мы можем еще раз проигнорировать изменение T 3/2 , которое в основном будет незначительным по сравнению с экспоненциальным изменением температуры.Таким образом, график зависимости ln (σ) от 1 / T будет иметь наклон –Eg / 2k, что дает значение для Eg.
В случае легированных полупроводников отметим, что при высоких температурах они являются внутренними по поведению и становятся псевдо-собственными при низких температурах, при этом энергетическая щель равна щели между примесным уровнем и краем зоны. Таким образом, на графике, аналогичном упомянутому выше, мы ожидаем двух прямолинейных участков с разными наклонами. В области между этими наклонами температура достаточно высока, чтобы полностью ионизировать доноры, но недостаточно высока, чтобы ионизировать значительное количество электронов из решетки.Следовательно, в этом температурном диапазоне плотность носителей не будет сильно зависеть от температуры, а подвижность, которой ранее пренебрегли, будет определять форму кривой.
Ссылки
- Bart van Zeghbroeck, Principles of Semiconductor Devices , Boulder, 2006
Преобразование температуры из Цельсия в Фаренгейта
Быстрый градус Цельсия ( ° C, ) / Фаренгейт ( ° F, ) Преобразование:Инструмент преобразования Просто введите значение в любое поле: Или используйте интерактивный термометр, Или этот метод:
(объяснение ниже…) |
Типичные температуры
| ° С | ° F | Описание | |
|---|---|---|---|
| 180 | 356 | Духовка среднего размера | |
| 100 | 212 | Вода закипает | |
| 40 | 104 | Горячая ванна | |
| 37 | 98.6 | Температура тела | |
| 30 | 86 | Погода на пляже | |
| 21 | 70 | Комнатная температура | |
| 10 | 50 | Прохладный день | |
| 0 | 32 | Температура замерзания воды | |
| −18 | 0 | Очень холодный день | |
| −40 | −40 | Extremely Cold Day (и столько же!) | |
| ( полужирный точно) | |||
16 около 61
28 около 82
Пояснение
Существуют две основные температурные шкалы:
- ° C , шкала Цельсия (часть метрической Система, используемая в большинстве стран)
- ° F , по шкале Фаренгейта (используется в США) и
Они оба измеряют одно и то же (температуру!), Но используют разные номера:
- Кипящая вода (при нормальном давлении) измеряет 100 ° по Цельсию, но 212 ° по Фаренгейту
- И замерзание воды измеряет 0 ° по Цельсию, но 32 ° по Фаренгейту
Как это:
Глядя на схему, обратите внимание:
- Шкалы начинаются с другого числа (0 против 32), поэтому мы будем нужно добавить или вычесть 32
- Шкала увеличивается с разной скоростью (100 против 180), поэтому мы также нужно умножить
Итак, преобразовать:
от Цельсия до Фаренгейта: сначала умножьте на 180 100 , затем добавьте 32
от Фаренгейта до Цельсия: сначала вычтите 32, затем умножьте по 100 180
180 100 можно упростить до 9 5 и 100 180 можно упростить до 5 9 , так что это самый простой способ:
от ° C до ° F: Разделите на 5, затем умножьте на 9, затем добавьте 32
от ° F до ° C: Вычтите 32, затем умножьте на 5, затем разделите на 9
.