Вязкость — ТеплоВики — энциклопедия отопления
Материал из ТеплоВики — энциклопедия отоплении
Вязкость (внутреннее трение) (англ. viscosity) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно. Основной закон вязкого течения был установлен И. Ньютоном (1687): В применении к жидкостям различают вязкость:
- Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.

- Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ.
где:
- ν, м2/с – кинематическая вязкость;
- μ, Па×с – динамическая вязкость;
- ρ, кг/м3 – плотность жидкости.
В системе СИ кинематическая вязкость выражается в м2/с (квадратный метр на секунду), внесистемная единица Ст(стокс).
Прибор для измерения вязкости называется вискозиметром.
Сила вязкого трения
Это явление возникновения касательных сил, препятствующих перемещению частей жидкости или газа друг по отношению к другу. Смазка между двумя твердыми телами заменяет сухое трение скольжения трением скольжения слоев жидкости или газа по отношению друг к другу. Скорость частиц среды плавно меняется от скорости одного тела до скорости другого тела.
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
F=-V•S/h,Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что при наличии любой сколь угодно малой силы тела придут в движение, то есть не существует трения покоя.
Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.
Если движущееся тело полностью погружено в вязкую среду и расстояния от тела до границ среды много больше размеров самого тела, то в этом случае говорят о трении или сопротивлении среды. При этом участки среды (жидкости или газа), непосредственно прилегающие к движущемуся телу, движутся с такой же скоростью, как и само тело, а по мере удаления от тела скорость соответствующих участков среды уменьшается, обращаясь в нуль на бесконечности.
Сила сопротивления среды зависит от:
- ее вязкости
- от формы тела
- от скорости движения тела относительно среды.
Например, при медленном движении шарика в вязкой жидкости силу трения можно найти, используя формулу Стокса:
F=-6•R•V,Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.
Вязкость газов
Вязкость газов (явление внутреннего трения) — это появление сил трения между слоями газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Вязкость газов увеличивается с ростом температуры
Взаимодействие двух слоев газа рассматривается как процесс, в ходе которого от одного слоя к другому передается импульс. Сила трения на единицу площади между двумя слоями газа, равная импульсу, передаваемому за секунду от слоя к слою через единицу площади, определяется законом Ньютона:
τ=-η•dν/dz
где:
dν/dz — градиент скорости в направлении перпендикулярном направлению движения слоев газа.
Знак минус указывает, что импульс переносится в направлении убывания скорости.
η — динамическая вязкость.
η=1/3•ρ(ν)•λ, где:
ρ — плотность газа,
(ν) — средняя арифметическая скорость молекул
λ — средняя длина свободного пробега молекул.
Вязкость некоторых газов (при 0°C)
| Вещество | Вязкость 10 -5 кг/(м*с) |
|---|---|
| Азот | 1,67 |
| Аммиак | 0,93 |
| Водород | 0,84 |
| Воздух | 1,72 |
| Гелий | 1,89 |
| Гелий | 1,89 |
| Кислород | 1,92 |
| Метан | 1,04 |
| Углекислый газ | 1,40 |
| Хлор | 1,29 |
Вязкость жидкости
Вязкость жидкости — это свойство, проявляющееся только при движении жидкости, и не влияющее на покоящиеся жидкости. Вязкое трение в жидкостях подчиняется закону трения, принципиально отличному от закона трения твёрдых тел, т.к. зависит от площади трения и скорости движения жидкости.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости. Если рассмотреть то, как распределяются скорости различных слоёв жидкости по сечению потока, то можно легко заметить, что чем дальше от стенок потока, тем скорость движения частиц больше. У стенок потока скорость движения жидкости равна нулю. Иллюстрацией этого является рисунок, так называемой, струйной модели потока.
Медленно движущийся слой жидкости «тормозит» соседний слой жидкости, движущийся быстрее, и наоборот, слой, движущийся с большей скоростью, увлекает (тянет) за собой слой, движущийся с меньшей скоростью. Силы внутреннего трения появляются вследствие наличия межмолекулярных связей между движущимися слоями. Если между соседними слоями жидкости выделить некоторую площадку S, то согласно гипотезе Ньютона:
F=μ•S•(du/dy),где:
- μ — коэффициент вязкого трения;
- S – площадь трения;
- du/dy — градиент скорости
Величина μ в этом выражении является динамическим коэффициентом вязкости, равным:
μ=F/S•1/du/dy,или
μ=τ•1/du/dy,где:
- τ – касательное напряжение в жидкости (зависит от рода жидкости).

Физический смысл коэффициента вязкого трения
Физический смысл коэффициента вязкого трения — число, равное силе трения, развивающейся на единичной поверхности при единичном градиенте скорости.
На практике чаще используется кинематический коэффициент вязкости, названный так потому, что в его размерности отсутствует обозначение силы. Этот коэффициент представляет собой отношение динамического коэффициента вязкости жидкости к её плотности:
ν=μ/Единицы измерения коэффициента вязкого трения:
- Н·с/м2;
- кГс·с/м2
- Пз (Пуазейль) 1(Пз)=0,1(Н·с/м2).
Анализ свойства вязкости жидкости
Для капельных жидкостей вязкость зависит от температуры t и давления Р, однако последняя зависимость проявляется только при больших изменениях давления, порядка нескольких десятков МПа.
Зависимость коэффициента динамической вязкости от температуры выражается формулой вида:
μt=μ0•e-kt(T-T0),где:
- μt — коэффициент динамической вязкости при заданной температуре;
- μ0 — коэффициент динамической вязкости при известной температуре;
- Т — заданная температура;
- Т0 — температура, при которой измерено значение μ0;
- e – основание натурального логарифма равное 2,718282.

Зависимость относительного коэффициента динамической вязкости от давления описывается формулой:
μр=μ0•e-kр(Р-Р0),где:
- μР — коэффициент динамической вязкости при заданном давлении,
- μ0 — коэффициент динамической вязкости при известном давлении (чаще всего при нормальных условиях),
- Р — заданное давление,;
- Р0 — давление, при которой измерено значение μ0;
- e – основание натурального логарифма равное 2,718282.
Влияние давления на вязкость жидкости проявляется только при высоких давлениях.
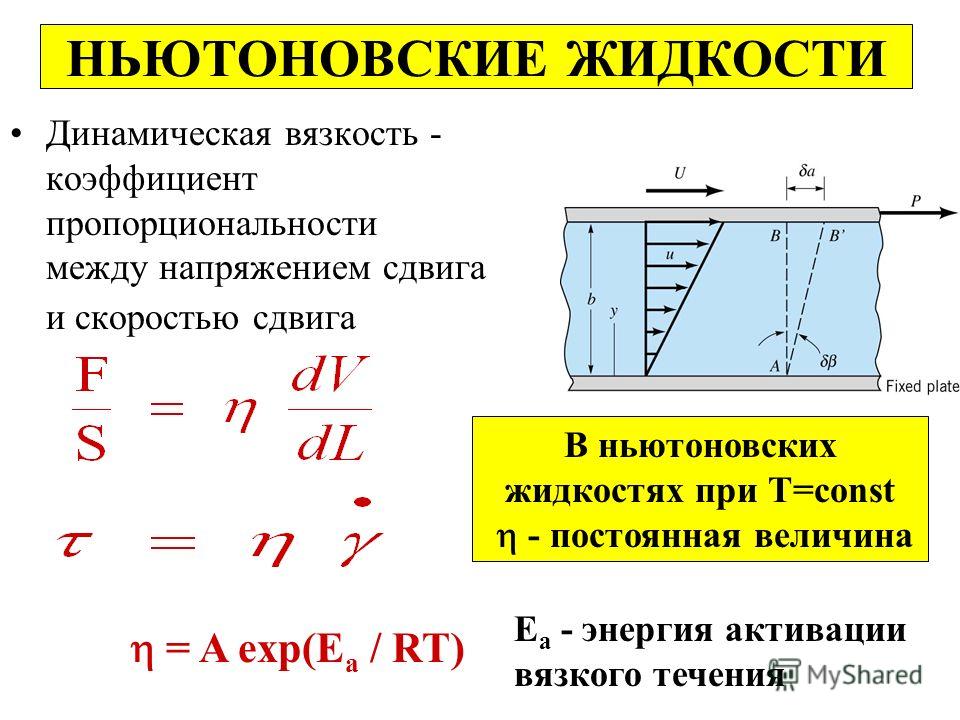
Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье):
где σij — тензор вязких напряжений.
Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.
Вязкость жидкостей (при 18°C)
| Вещество | Вязкость 10 -5 кг/(м*с) |
|---|---|
| Анилин | 4,6 |
| Ацетон | 0,337 |
| Бензол | 0,673 |
| Бром | 1,02 |
| Вода | 1,05 |
| Гелий | 1,89 |
| Глицерин | 1400 |
| Масло машинное легкое | 113 |
| Масло машинное тяжелое | 660 |
| Масло оливковое | 90 |
| Масло оливковое | 90 |
| Пентан | 0,244 |
| Ртуть | 1,59 |
| Спирт этиловый | 1,22 |
| Уксусная кислота | 1,27 |
| Эфир этиловый | 0,238 |
См. также
также
Источники
Вязкость — ТеплоВики — энциклопедия отопления
Материал из ТеплоВики — энциклопедия отоплении
Вязкость (внутреннее трение) (англ. viscosity) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно. Основной закон вязкого течения был установлен И. Ньютоном (1687): В применении к жидкостям различают вязкость:
- Динамическая (абсолютная) вязкость µ – сила, действующая на единичную площадь плоской поверхности, которая перемещается с единичной скоростью относительно другой плоской поверхности, находящейся от первой на единичном расстоянии.
 В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз).
В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз). - Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ.
где:
- ν, м2/с – кинематическая вязкость;
- μ, Па×с – динамическая вязкость;
- ρ, кг/м3 – плотность жидкости.
В системе СИ кинематическая вязкость выражается в м2/с (квадратный метр на секунду), внесистемная единица Ст(стокс).
Прибор для измерения вязкости называется вискозиметром.
Сила вязкого трения
Это явление возникновения касательных сил, препятствующих перемещению частей жидкости или газа друг по отношению к другу. Смазка между двумя твердыми телами заменяет сухое трение скольжения трением скольжения слоев жидкости или газа по отношению друг к другу. Скорость частиц среды плавно меняется от скорости одного тела до скорости другого тела.
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.
F=-V•S/h,Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что при наличии любой сколь угодно малой силы тела придут в движение, то есть не существует трения покоя.
Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.
Если движущееся тело полностью погружено в вязкую среду и расстояния от тела до границ среды много больше размеров самого тела, то в этом случае говорят о трении или сопротивлении среды. При этом участки среды (жидкости или газа), непосредственно прилегающие к движущемуся телу, движутся с такой же скоростью, как и само тело, а по мере удаления от тела скорость соответствующих участков среды уменьшается, обращаясь в нуль на бесконечности.
Сила сопротивления среды зависит от:
- ее вязкости
- от формы тела
- от скорости движения тела относительно среды.
Например, при медленном движении шарика в вязкой жидкости силу трения можно найти, используя формулу Стокса:
F=-6•R•V,Качественно существенное отличие сил вязкого трения от сухого трения, кроме прочего, то, что тело при наличии только вязкого трения и сколь угодно малой внешней силы обязательно придет в движение, то есть для вязкого трения не существует трения покоя, и наоборот — под действием только вязкого трения тело, вначале двигавшееся, никогда (в рамках макроскопического приближения, пренебрегающего броуновским движением) полностью не остановится, хотя движение и будет бесконечно замедляться.
Вязкость газов
Вязкость газов (явление внутреннего трения) — это появление сил трения между слоями газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Вязкость газов увеличивается с ростом температуры
Взаимодействие двух слоев газа рассматривается как процесс, в ходе которого от одного слоя к другому передается импульс. Сила трения на единицу площади между двумя слоями газа, равная импульсу, передаваемому за секунду от слоя к слою через единицу площади, определяется законом Ньютона:
τ=-η•dν/dz
где:
dν/dz — градиент скорости в направлении перпендикулярном направлению движения слоев газа.
Знак минус указывает, что импульс переносится в направлении убывания скорости.
η — динамическая вязкость.
η=1/3•ρ(ν)•λ, где:
ρ — плотность газа,
(ν) — средняя арифметическая скорость молекул
λ — средняя длина свободного пробега молекул.
Вязкость некоторых газов (при 0°C)
| Вещество | Вязкость 10 -5 кг/(м*с) |
|---|---|
| Азот | 1,67 |
| Аммиак | 0,93 |
| Водород | 0,84 |
| Воздух | 1,72 |
| Гелий | 1,89 |
| Гелий | 1,89 |
| Кислород | 1,92 |
| Метан | 1,04 |
| Углекислый газ | 1,40 |
| Хлор | 1,29 |
Вязкость жидкости
Вязкость жидкости — это свойство, проявляющееся только при движении жидкости, и не влияющее на покоящиеся жидкости. Вязкое трение в жидкостях подчиняется закону трения, принципиально отличному от закона трения твёрдых тел, т.к. зависит от площади трения и скорости движения жидкости.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости. Если рассмотреть то, как распределяются скорости различных слоёв жидкости по сечению потока, то можно легко заметить, что чем дальше от стенок потока, тем скорость движения частиц больше. У стенок потока скорость движения жидкости равна нулю. Иллюстрацией этого является рисунок, так называемой, струйной модели потока.
Медленно движущийся слой жидкости «тормозит» соседний слой жидкости, движущийся быстрее, и наоборот, слой, движущийся с большей скоростью, увлекает (тянет) за собой слой, движущийся с меньшей скоростью. Силы внутреннего трения появляются вследствие наличия межмолекулярных связей между движущимися слоями. Если между соседними слоями жидкости выделить некоторую площадку S, то согласно гипотезе Ньютона:
F=μ•S•(du/dy),где:
- μ — коэффициент вязкого трения;
- S – площадь трения;
- du/dy — градиент скорости
Величина μ в этом выражении является динамическим коэффициентом вязкости, равным:
μ=F/S•1/du/dy,или
μ=τ•1/du/dy,где:
- τ – касательное напряжение в жидкости (зависит от рода жидкости).

Физический смысл коэффициента вязкого трения
Физический смысл коэффициента вязкого трения — число, равное силе трения, развивающейся на единичной поверхности при единичном градиенте скорости.
На практике чаще используется кинематический коэффициент вязкости, названный так потому, что в его размерности отсутствует обозначение силы. Этот коэффициент представляет собой отношение динамического коэффициента вязкости жидкости к её плотности:
ν=μ/ρ,Единицы измерения коэффициента вязкого трения:
- Н·с/м2;
- кГс·с/м2
- Пз (Пуазейль) 1(Пз)=0,1(Н·с/м2).
Анализ свойства вязкости жидкости
Для капельных жидкостей вязкость зависит от температуры t и давления Р, однако последняя зависимость проявляется только при больших изменениях давления, порядка нескольких десятков МПа.
Зависимость коэффициента динамической вязкости от температуры выражается формулой вида:
μt=μ0•e-kt(T-T0),где:
- μt — коэффициент динамической вязкости при заданной температуре;
- μ0 — коэффициент динамической вязкости при известной температуре;
- Т — заданная температура;
- Т0 — температура, при которой измерено значение μ0;
- e – основание натурального логарифма равное 2,718282.

Зависимость относительного коэффициента динамической вязкости от давления описывается формулой:
μр=μ0•e-kр(Р-Р0),где:
- μР — коэффициент динамической вязкости при заданном давлении,
- μ0 — коэффициент динамической вязкости при известном давлении (чаще всего при нормальных условиях),
- Р — заданное давление,;
- Р0 — давление, при которой измерено значение μ0;
- e – основание натурального логарифма равное 2,718282.
Влияние давления на вязкость жидкости проявляется только при высоких давлениях.
Ньютоновские и неньютоновские жидкости
Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. В уравнении Навье — Стокса для ньютоновской жидкости имеет место аналогичный вышеприведённому закон вязкости (по сути, обобщение закона Ньютона, или закон Навье):
σij=η•(dvi/dxi+dvj/dxi),где σij — тензор вязких напряжений.
Среди неньютоновских жидкостей, по зависимости вязкости от скорости деформации различают псевдопластики и дилатантные жидкости. Моделью с ненулевым напряжением сдвига (действие вязкости подобно сухому трению) является модель Бингама. Если вязкость меняется с течением времени, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.
С повышением температуры вязкость многих жидкостей падает. Это объясняется тем, что кинетическая энергия каждой молекулы возрастает быстрее, чем потенциальная энергия взаимодействия между ними. Поэтому все смазки всегда стараются охладить, иначе это грозит простой утечкой через узлы.
Вязкость жидкостей (при 18°C)
| Вещество | Вязкость 10 -5 кг/(м*с) |
|---|---|
| Анилин | 4,6 |
| Ацетон | 0,337 |
| Бензол | 0,673 |
| Бром | 1,02 |
| Вода | 1,05 |
| Гелий | 1,89 |
| Глицерин | 1400 |
| Масло машинное легкое | 113 |
| Масло машинное тяжелое | 660 |
| Масло оливковое | 90 |
| Масло оливковое | 90 |
| Пентан | 0,244 |
| Ртуть | 1,59 |
| Спирт этиловый | 1,22 |
| Уксусная кислота | 1,27 |
| Эфир этиловый | 0,238 |
См. 2/2
2/2Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Вязкость жидкостей. Динамическая и кинематическая вязкость. Число Рейнольдса. Ламинарное и турбулентное течение. Методы определения вязкости.
Вязкость — сопротивление жидкости передвижению одного ее слоя относительно другого.
Динамической вязкостью называется свойство жидкостей, характеризующее их сопротивляемость скольжению или сдвигу. Именно динамический коэффициент вязкости измеряется в пуазах.
Кинематическая вязкость равна отношению динамической вязкости к плотности при той же температуре. Измеряется в стоксах.
Число Рейнольдса — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
Методы определения вязкости:
а)метод Стокса
При движении тела в вязкой среде возникают силы сопротивления. Происхождение этого сопротивления двояко.
При небольших скоростях, когда за телом нет вихрей (то есть обтекание тела ламинарное), сила сопротивления обуславливается вязкостью среды. Между движущимся телом и средой существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы прилипая к телу. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Для ламинарного потока сила трения пропорциональна скорости тела: . Теоретический расчет внутреннего трения для движения шарикав вязкой среде с небольшой скоростью, когда нет вихрей, приводит к формуле Стокса:
, где – радиус шарика, – скорость его движения, – коэффициент динамической вязкости среды.
б)формула Пуазейля
Ламинарный параллельный поток имеет место, например, при медленном протекании газа в цилиндрической трубе (капилляре) – в этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.
Выделим в капилляре воображаемый цилиндрический объем жидкости (или газа) радиусом и длиной , как показано на рисунке 5.9. Обозначим давления на его торцах и . При установившемся течении суммарная сила давления на цилиндр.
Формула называется формулой Пуазейля. Она позволяет экспериментально определить динамическую вязкость жидкости (газа), измерив объёмный расход и зная разность давлений на концах капилляра и его геометрические параметры.
В гладких цилиндрических каналах переход от ламинарного течения к турбулентному происходит при . Поэтому в случае использования формулы Пуазейля необходимо обеспечить выполнение условия .
Ламинарное течение — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).
Турбулентное течение — форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа.
Вязкость (внутреннее трение) (см. лекцию №5 «Элементы механики жидкостей и газов») возникает между слоями газа или жидкости, движущимися с разными скоростями. Если скорость направленного движения слоёв газа изменяется вдоль оси OZ (рис.7.6), то по закону Ньютона, импульс, перенесённый через малую площадку за время , пропорционален градиенту скорости направленного движения слоёв :
, (7.13)
где – динамическая вязкость. Быстрый слой при этом тормозится, медленный – ускоряется в результате действия силы вязкого трения:
.
Из (7.13) физический смысл динамической вязкости: коэффициент вязкости численно равен импульсу, перенесённому из слоя в слой через единичную площадку за единицу времени при единичном градиенте скорости направленного движения слоёв. Размерность коэффициента вязкости:
.
Плотность потока импульса (импульс, перенесённый за единицу времени через единичную площадку) равна
. (7.14)
Билет
Вязкость — Студопедия
Вязкость – это свойство жидкости оказывать сопротивление сдвигающим усилиям. Вязкость — свойство, присущее как капельным жидкостям, так и газам, которое проявляется только при движении, не может быть обнаружено при покое, и проявляется в виде внутреннего трения при перемещении смежных частиц жидкости. Вязкость характеризует степень текучести жидкости и подвижности ее частиц. Вязкостью жидкостей объясняется сопротивление и потери напор, которое возникает при движении их по трубам, каналам и прочим руслам, а также при движении в них инородных тел.
Изучение свойств внутреннего трения жидкости активно занимался Исаак Ньютон, заложив основы учению о вязкости. Ньютон высказал предположение (впоследствии подтвержденное опытом), что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. В итоге, И. Ньютон получил зависимость, характеризующую связь вязкости с явлением внутреннего трения, получившую название одноименного закона.
Пусть жидкость течет вдоль плоской стенки параллельными слоями. Каждый слой будет двигаться со своей скоростью, причем скорость слоев будет увеличиваться по мере отдаления от стенки.
Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга. Поскольку между слоями присутствует сила трения и благодаря взаимному торможению различные слои имеют различные скорости, и слой А движется со скоростью v, а слой Б – со скоростью (v+Δv). Величина Δv является абсолютным сдвигом слоя А по слою Б, а величина Δv/Δy – относительным сдвигом, или градиентом скорости. Тогда при движении возникает касательное напряжение τ (тау), которое характеризует трение на единицу площади (напряжением внутреннего трения).
Тогда при движении возникает касательное напряжение τ (тау), которое характеризует трение на единицу площади (напряжением внутреннего трения).
Напряжение внутреннего трения имеет физический смысл зависимости:
,
где Fтр – сила внутреннего трения, Н; S – площадь соприкосновения поверхностей, м2.
Тогда согласно закону Ньютона зависимость между напряжением и относительным сдвигом будет иметь вид:
,
т.е. напряжение внутреннего трения пропорционального градиенту скорости.
Коэффициент пропорциональности µ (мю) называется динамическим коэффициентом вязкости. Из формулы видно, что динамический коэффициент вязкости численно равен напряжению внутреннего трения в том случае, когда относительная скорость двух плоскостей А и Б, отстоящих друг от друга на расстоянии 1 м, равна 1м/с.
Размерность динамического коэффициента вязкости следует из формулы. Так как напряжение τ есть сила, отнесенная к единице площади, то его размерность равна:
.
Размерность градиента скорости:
.
Отсюда размерность динамического коэффициента вязкости:
.
Таким образом, за единицу измерения динамической вязкости в системе единиц СИ принимают:
.
В физической системе единицей динамической вязкости является пуаз, обозначается «П»:
.
Динамическая вязкость у капельных жидкостей, молекулы которых расположены весьма близко друг к другу, при повышении температуры уменьшается в связи с увеличением скорости броуновского движения, ослабляющего удерживающие связи, то есть силы сцепления.
Зависимость коэффициента μ от температуры в общем виде выражается формулой:
,
где — значение при t = 0°C; а и b — опытные коэффициенты, зависящие от физико-химических свойств (от рода) жидкости; t — температура жидкости в °С.
У газов силы притяжения между молекулами проявляют себя только при сильном сжатии, а в обычных условиях молекулы газов находятся в состоянии хаотичного теплового движения и трение слоев газа друг о друга происходит только вследствие столкновения молекул. При повышении температуры скорость молекул возрастает, растет число их столкновений и вязкость возрастает.
При повышении температуры скорость молекул возрастает, растет число их столкновений и вязкость возрастает.
Для пресной воды Пуазейлем получена формула:
. (1.3)
Для воздуха известна формула Милликена:
. (1.4)
В гидравлике для характеристики вязких свойств газов и паров иногда вместо динамического употребляется другой коэффициент вязкости, обозначаемый буквой η (эта) и связанный с динамическим коэффициентом уравнением
, (1.5)
где g – ускорение силы тяжести, м/с2.
Очевидно, этот коэффициент вязкости η имеет размерность:
.
При этом единицей измерения η в технической системе единиц является
.
В гидравлике и на производстве широко применяется так называемый кинематический коэффициент вязкости ν (ню), определяемый как отношение динамической вязкости к плотности:
.
Размерность кинематического коэффициента вязкости:
.
В системе СИ для ν принята единица: .
Единицей измерения коэффициента ν в физической системе служит стокс, обозначается «Ст»:
.
Например, кинематический коэффициент вязкости воды равен
.
Величину, обратную динамической вязкости называют текучестью.
Вязкость для всех капельных жидкостей убывает с повышением температуры. Для получения точных гидравлических расчетов рекомендуется иметь график (или таблицу) зависимости вязкости от температуры, построенный на основе специальных определений в лаборатории. Весьма осторожно следует относиться к различного рода номограммам и формулам, служащим для определения вязкости смеси двух или нескольких различных нефтепродуктов.
График, характеризующий зависимость изменения вязкости жидкости от температуры называется вискограммой (Рис. 1.3).
Рис.1.3. Вискограмма
Для определения вязкости жидкости при любой произвольной температуре T с достаточной точностью используется формула Рейнольдса-Филонова:
,
где ν — вязкость при известной температуре Т, u – коэффициент крутизны вискограммы, который характеризует угол наклона касательной вискограммы к оси абсцисс (Рис. 1.4) и определяется по формуле:
1.4) и определяется по формуле:
.
Рис.1.4 Определение коэффициента крутизны вискограммы
Таким образом, можно охарактеризовать любую жидкость и определить ее вязкость при любой температуре, зная координаты двух произвольных точек вискограммы. Стоит заметить, что для капельных жидкостей коэффициент вискограммы положителен, однако существуют жидкости, у которых вязкость мало изменяется при изменении температуры, для газообразных — коэффициент вискограммы отрицателен. Существуют жидкости, вязкость которых мало зависит от температуры, они представляют собой сложные химические соединения и используются в качестве рабочих в гидравлических машинах, например в вискомуфтах.
Существуют жидкости, для которых закон И. Ньютона неприменим. В отличие от обычных, ньютоновских, эти жидкости называют неньютоновскими, или аномальными.
Значения кинематической вязкости ν воды и воздуха
t,0C 106ν, м2/c воды воздуха 1,78 13,7 1,31 14,7 1,01 15,7 0,81 16,6 0,66 17,6 0,48 19,6 0,28 23,8
Таблица 1. 6
6
Кинематическая вязкость некоторых жидкостей
Жидкость t, °C v?10-4, м2/с Жидкость t, °C v?10-4, м2/с Бензин 0,0065 Ртуть 0,00125 Спирт винный 0,0133 Сталь жидкая (0,3% С) 0,00370 Керосин 0,0250 Глицерин 8,7000
Вязкость различных сортов жидкости одного названия, например, нефти, в зависимости от химического состава и молекулярного строения может иметь различные значения.
Для вязких нефтей средние значения u = 0,05 + 0,1 на 1°С.
Вязкость жидкостей, как показывают опыты, зависит также от давления. При возрастании давления она обычно увеличивается. Исключением является вода, для которой при температуре до 32° С с повышением давления вязкость уменьшается. При давлениях, встречающихся в практике (до 20 МПа), изменение вязкости жидкостей весьма мало и при обычных гидравлических расчетах не учитывается.
При давлениях, встречающихся в практике (до 20 МПа), изменение вязкости жидкостей весьма мало и при обычных гидравлических расчетах не учитывается.
методы определения коэффициента, что является причиной, формула с примерами
Что такое вязкость жидкости
Определение Число Рейнольдса также считается критерием подобия течения вязкой жидкости.
Число Рейнольдса также считается критерием подобия течения вязкой жидкости.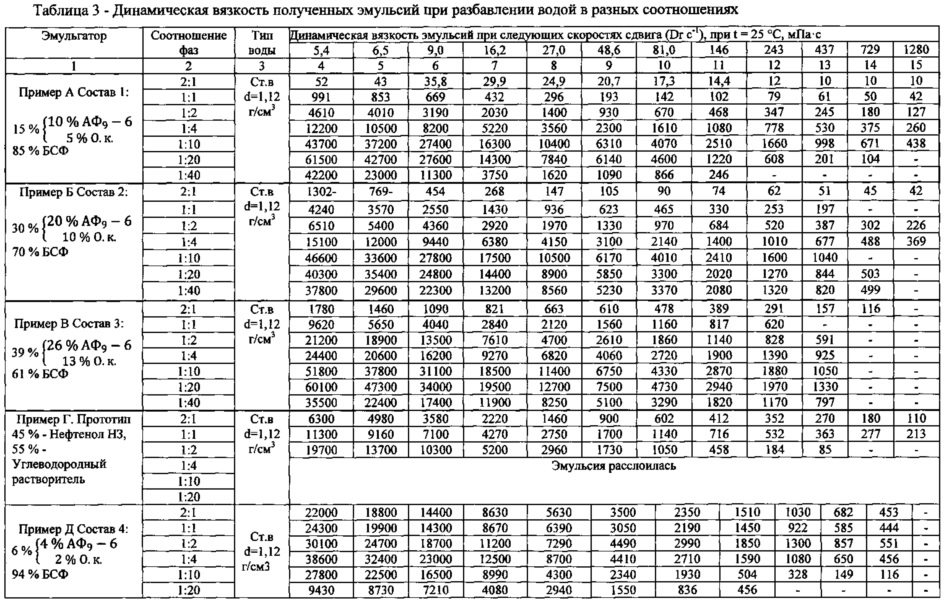



 Тогда при движении возникает касательное напряжение τ (тау), которое характеризует трение на единицу площади (напряжением внутреннего трения).
Тогда при движении возникает касательное напряжение τ (тау), которое характеризует трение на единицу площади (напряжением внутреннего трения).
 При повышении температуры скорость молекул возрастает, растет число их столкновений и вязкость возрастает.
При повышении температуры скорость молекул возрастает, растет число их столкновений и вязкость возрастает.
 1.4) и определяется по формуле:
1.4) и определяется по формуле: 6
6 При давлениях, встречающихся в практике (до 20 МПа), изменение вязкости жидкостей весьма мало и при обычных гидравлических расчетах не учитывается.
При давлениях, встречающихся в практике (до 20 МПа), изменение вязкости жидкостей весьма мало и при обычных гидравлических расчетах не учитывается.Вязкость жидкости — свойство реальных жидкостей оказывать сопротивление касательным усилиям (внутреннему трению) в потоке.
Причина возникновения этого явления — сопротивление молекул жидкости относительно друг друга при движении. Это внутреннее трение, возникающее между частицами в процессе их перемещения.
Его сила имеет зависимость от нескольких факторов:
- температуры жидкости;
- скорости движения;
- времени;
- химического состава.
Реже на вязкость оказывает влияние давление — только при увеличении его до 1000—1200 МПа.
Разновидности вязкости
Динамическая (абсолютная) вязкость, а точнее её коэффициент ƞ, вычисляется с помощью формулы:
\(\eta\;=\;r\;/\;(dv/dr)\)
Где r — сила вязкого сопротивления между соседними слоями жидкости, направленная вдоль их поверхности, а \(dv/dr\) — градиент их относительной скорости, взятый по направлению, перпендикулярному к направлению движения.
Размеренность динамической вязкости ML-1T-1, ее единицей в системе СГС служит пуаз (пз) = 1г/см*сек=1дин*сек/см2=100 сантипуазам (спз).
Пуаз показывает изменение потерь давления за определённое время. При увеличении температуры динамическая вязкость уменьшается.
Кинематическая вязкость зависит от плотности вещества. Она рассчитывается по формуле:
\( v=\frac{\eta}{P}\)
Где p — плотность вещества, η — динамическая вязкость.
Величиной измерения кинематической вязкости считаются сантистоксы (сСт). Их можно перевести в стандартную систему измерения следующим образом: 1 сСт = 1 мм2/c = 10−6 м2/c.
Методы измерения
Существует четыре способа измерения коэффициента вязкости:
- Вибрационный. Специальный прибор — вискозиметр — погружают в исследуемую среду. Показателем вязкости будет частота вибраций зонда, погруженного в жидкость.

- Ротационный. Ротационный вискозиметр определяет величину вязкости с помощью определения вращающего момента цилиндрических роторов, опущенных в образец жидкости. Величина вязкости пропорциональна вращающему моменту.
- Капиллярный. Вискозиметр представляет собой колбу, через которую за определенное время протекает исследуемая жидкость. Разница давлений на концах трубки определяет величину вязкости жидкости.
- Метод падающего шарика или метод Стокса. В вискозиметр с жидкостью опускают цилиндрический или круглый предмет. Время, за которое шарик достиг определённой отметки внутри вискозиметра будет показывать вязкость воды. При этом плотность и объем самого объекта заранее известны.
Понятие вязкости жидкости широко применяется в медицине, перерабатывающей промышленности, в лабораторных исследованиях.
Динамическая и кажущаяся вязкость.
ЛЕКЦИЯ 4
Биореология
План лекции
Ньютоновские и неньютоновские жидкости.
 Уравнение
Ньютона.
Уравнение
Ньютона.Динамическая и кажущаяся вязкость. Уравнение Шведова – Бингама.
Уравнение Бернулли.
Движение жидкости по трубам. Скорость течения.
Закон Пуазейля. Гидравлическое (периферическое) сопротивление.
Ламинарное и турбулентное течение. Число Рейнольдса.
Реологические свойства крови.
Ньютоновские и неньютоновские жидкости.
Уравнение Ньютона.
Реология – это раздел физики, изучающий силы сопротивления, возникающие в движущихся жидкостях и газах.
Жидкости не имеют своей формы. Они принимают всегда форму того сосуда, в котором они находятся. Основным параметром жидкости является её плотность m/V (кг\м3).
В жидкостях и в газах действует закон Паскаля: жидкости и газы передают давление во все стороны одинаково. То есть, если в какой-либо части объёма жидкости мы попытаемся повысить давление, то оно сразу распространится на весь объём жидкости. Величина давления измеряется в паскалях (Па) или Н\м2. т.е. Р = F/S.
Представим себе, что внутри жидкости движется некоторая плоскость, причём, вектор её скорости направлен параллельно данной плоскости.
Слой жидкости, непосредственно прилегающий к этой плоскости, движется вместе с плоскостью с той же скоростью Отступив от плоскости на расстояние Y мы заметим, что скорость жидкости на этом расстоянии уменьшилась на величину . Таким образом, скорость слоёв жидкости уменьшается пропорционально увеличению расстояния от плоскости. Введём величину, которую назовём градиентом скорости:
grad Y
Исаак Ньютон установил, что сила сопротивления, возникающая при движении тела в жидкости, пропорциональна градиенту скорости и величине плоскости:
F = —Y)S
Это – уравнение Ньютона. Коэффициент называется коэффициентом вязкости или динамической вязкостью. Он измеряется в Па . с .
Коэффициент вязкости у каждой жидкости имеет своё собственное значение.
Он также зависит от температуры жидкости и не зависит от скорости сдвига.
Те жидкости, которые подчиняются уравнению Ньютона, называются идеальными или ньютоновскими. К ним относятся такие жидкости, как вода, одноатомные спирты, эфир, бензин, керосин, минеральное масло, и др.
Однако существуют жидкости, которые не подчиняются уравнению Ньютона и при подсчёте силы сопротивления по формуле Ньютона получается большая погрешность. Такие жидкости в своём составе имеют либо высокомолекулярные соединения, либо представляют собой эмульсии, суспензии различных форменных элементов. Например, яичный белок сырого яйца, кисель, молоко и его продукты, кровь и т.д.Их вязкость значительно больше.
Уравнение Шведова – Бингама.
Для того, чтобы понять следующий раздел, вспомним один из видов деформации твёрдого тела: деформацию сдвига. Представим себе куб, сделанный из какого-либо твёрдого тела. Приложим к его верхней грани сдвигающую силу F. Отношение этой силы к величине площади верхней грани S называется сдвиговым напряжением (Н\м2) .
F/S=— напряжение сдвига
dv/dx= — градиент сдвиговой скорости.
Шведов и Бингам установили связь между сдвиговой скоростью и напряжением сдвига. Они вывели уравнение, которое носит их имя:
M
Здесь:
— предел текучести, т.е. минимальное напряжение, при котором жидкость начинает течь. По аналогии с твёрдым телом, — это такое сдвиговое напряжение, при котором тело перестаёт восстанавливать свою форму после снятия деформирующей нагрузки.
M — структурная вязкость. Она более полно отображает вязкость жидкостей. Например, при движении крови по сосудам, вязкость зависит не только от форменных элементов, но и от эластичности стенок сосуда.
При увеличении скорости движения жидкости структурная вязкость стремится к определённому пределу, который называется кажущейся вязкостью:
Графически изобразить уравнения Шведова – Бингама можно следующим графиком:
Следует отметить, что для ньютоновских жидкостей равно нулю. Это значит, что в ньютоновских жидкостях сила трения покоя отсутствует полностью. Это можно обнаружить на таком примере. Предположим, что на поверхности абсолютно спокойной воды плавает какой-либо тяжёлый предмет (бревно). А вода является ньютоновской жидкостью, следовательно, плавающее тело можно привести в движение самой маленькой силой. Тоже бревно, лежащее на берегу, с места сдвинуть очень трудно, так как сила трения покоя при движении по поверхности твёрдого тела имеет значительную величину. Отсутствие в таких жидкостях силы трения покоя используется в точных навигационных приборах: компасах, гироскопах и пр. Следует добавить, что если ньютоновскую жидкость вылить на блюдце, то её поверхность сразу приобретает форму горизонтальной плоскости. С неньютоновской жидкостью наблюдается другая картина. Возьмём жидкость, являющуюся наиболее ярким представителем неньютоновских жидкостей: яичный белок. Если его вылить на блюдце, то его поверхность будет иметь форму небольшой горки, так как сила тяжести не в состоянии преодолеть до конца предел текучести жидкости.
Для очистки жидкостей от механических примесей используют фильтр из специальной пористой бумаги или ваты. Если нам приходится фильтровать воду, то мы заметим, что для фильтрации необходимо некоторое время. Если мы вместо воды возьмём спирт или бензин, то они через тот же фильтр будут профильтровываться быстрее, особенно бензин. Ведь чем меньше вязкость жидкости – тем быстрее она фильтруется. Надо сказать, что поддаются фильтрации все ньютоновские жидкости, даже такие, у которых высокая вязкость. Например, растительное масло будет тоже фильтроваться, но процесс фильтрации будет проходить медленно. А что будет, если мы попытаемся фильтровать неньютоновскую жидкость? Мы знаем, что наиболее ярким представителем ньютоновских жидкостей является яичный белок сырого яйца. Мы можем даже без практического опыта догадаться, что яичный белок вообще фильтроваться не будет, так как у него очень большой предел текучести. Не будут фильтроваться также и кисломолочные продукты. Строго говоря, все неньютоновские жидкости могут подвергаться процессу фильтрации, но для этого нужно их прогонять через фильтр действием дополнительной внешней силой. А силы тяжести для этого будет явно недостаточно.
Воздух — динамическая и кинематическая вязкость
Вязкость жидкости является мерой ее сопротивления постепенной деформации под действием напряжения сдвига или растягивающего напряжения .
Для получения дополнительных определений перейдите к Абсолютная (динамическая) и кинематическая вязкость . Абсолютная или динамическая вязкость используется для расчета числа Рейнольдса, чтобы определить, является ли поток жидкости ламинарным, переходным или турбулентным.
Табличные значения и преобразование единиц вязкости приведены под рисунками.
Онлайн-калькулятор вязкости воздуха
Калькулятор, представленный ниже, можно использовать для расчета динамической или кинематической вязкости воздуха при заданной температуре и атмосферном давлении.
Выходная динамическая вязкость выражается в Па * с, Н * с / м 2 , сП, мПа * с, фунт ф * с / фут 2 и фунт м / (фут * ч),
, а кинематическая вязкость выражена в сСт, м 2 / с и фут 2 / с
Примечание! Температура должна быть в пределах -100 — 1600 ° C, -150 — 2900 ° F, 175 — 1900 K и 310-3400 ° R, чтобы получить действительные значения.
Температура
Выберите фактическую единицу измерения температуры:° C ° F K ° R
См. Также другие свойства Air при различных температуре и давлении: Плотность и удельный вес при различной температуре , Плотность при переменном давлении, коэффициенты диффузии для газов в воздухе, число Прандтля, удельная теплоемкость при различной температуре и удельная теплоемкость при переменном давлении, теплопроводность, теплопроводность, свойства в условиях равновесия газ-жидкость и теплофизические свойства воздуха при стандартных условиях и составе. и молекулярная масса
, а также динамическая и кинематическая вязкость аммиака, бензола, бутана, диоксида углерода, этана, этанола, этилена, метана, метанола, азота, кислорода, пропана и воды.
Динамическая и кинематическая вязкость воздуха при атмосферном давлении и переменной температуре:
Наверх
Динамическая вязкость воздуха при переменной температуре и постоянном давлении (1-10 000 бар абс., 14,5 — 145 000 фунтов на квадратный дюйм):
Вернуться к началу
Кинематическая вязкость воздуха при переменной температуре и постоянном давлении (1-10 000 бар, 14,5 — 145 000 фунтов на кв. Дюйм):
Вернуться к началу
Динамическая и кинематическая вязкость воздуха при равновесном давлении газ-жидкость:
Вернуться к началу
Динамическая (абсолютная) и кинематическая вязкость воздуха при давлении 1 атмосфера, при температурах, указанных в ° F:
Для полного стола с кинематической вязкостью — поверните экран!
| Температура | Динамическая вязкость | Кинематическая вязкость | ||||||
| [° F] | [фунт фут сек / фут 2 * 10 -6 ] | [фунт м / фут ч] | [мкПа с], [Н с / м 2 * 10 -6 ] | [сП], [мПа с] | [футов 2 / с * 10 -4 ] | [сСт], [м 2 / с * 10 -6 ] | ||
| -100 | 0.2772 | 0,03211 | 13,27 | 0,01327 | 0,809 | 7,51 | ||
| -50 | 0,3091 | 0,03580 | 14,80 | 0,01480 | 1,028 | 9,55 | ||
| -9,55 | ||||||||
| 0,03794 | 15,68 | 0,01568 | 1,170 | 10,87 | ||||
| 0 | 0,3395 | 0,03932 | 16.25 | 0,01625 | 1,267 | 11,77 | ||
| 10 | 0,3454 | 0,04001 | 16,54 | 0,01654 | 1,317 | 12,24 | ||
| 20 | 0,3512 | 0,040682 | 0,040682 | 0,0406821,368 | 12,71 | |||
| 30 | 0,3570 | 0,04135 | 17,10 | 0,01710 | 1.420 | 13,19 | ||
| 40 | 0,3628 | 0,04202 | 17,37 | 0,01737 | 1,472 | 13,67 | ||
| 50 | 0,3685 | 0,04268 | 141764 | 1,5|||||
| 60 | 0,3741 | 0,04333 | 17,91 | 0,01791 | 1,578 | 14,66 | ||
| 70 | 0.3797 | 0,04398 | 18,18 | 0,01818 | 1,632 | 15,16 | ||
| 80 | 0,3852 | 0,04462 | 18,45 | 0,01845 | 1,687 | 15,67 | ||
| 0,0187 | 18,97 | 0,01897 | 1,799 | 16,71 | ||||
| 120 | 0,4069 | 0,04713 | 19.48 | 0,01948 | 1,913 | 17,78 | ||
| 140 | 0,4175 | 0,04835 | 19,99 | 0,01999 | 2,030 | 18,86 | ||
| 160 | 0,4279 | 0,04956 | 160 | 0,4279 | 0,04956 0,04956 | 2,150 | 19,97 | |
| 180 | 0,4381 | 0,05074 | 20,98 | 0,02098 | 2.272 | 21,11 | ||
| 200 | 0,4481 | 0,05191 | 21,46 | 0,02146 | 2,397 | 22,27 | ||
| 250 | 0,4726 | 0,05474 | 22,63 | 900,05474 | 22,63 | 900,05474 | 22,63 | 900,05 |
| 300 | 0,4962 | 0,05747 | 23,76 | 0,02376 | 3,055 | 28,38 | ||
| 350 | 0.5189 | 0,06010 | 24,85 | 0,02485 | 3,405 | 31,64 | ||
| 400 | 0,5409 | 0,06265 | 25,90 | 0,02590 | 3,769 | 35,02 | ||
| 45090 0,025 | 26,92 | 0,02692 | 4,146 | 38,52 | ||||
| 500 | 0,5828 | 0,06751 | 27.91 | 0,02791 | 4,535 | 42,13 | ||
| 600 | 0,6224 | 0,07209 | 29,80 | 0,02980 | 5,349 | 49,70 | ||
| 700 | 0,6600 | 0,076446090 | 0,6600 | 0,076446090 900 | 6,209 | 57,68 | ||
| 773 | 0,6863 | 0,07949 | 32,86 | 0,03286 | 6.864 | 63,77 | ||
| 1000 | 0,7632 | 0,08840 | 36,54 | 0,03654 | 9,038 | 83.97 | ||
| 1200 | 0,8258 | 0,09565 | 39,54 | 0,09565 | 39,54 | 0,09 | ||
| 1400 | 0,8844 | 0,1024 | 42,35 | 0,04235 | 13,34 | 123,9 | ||
| 1600 | 0.9397 | 0,1088 | 44,99 | 0,04499 | 15,70 | 145,8 | ||
| 1800 | 0,9919 | 0,1149 | 47,49 | 0,04749 | 18,18 | 168.9 | ||
| 49,87 | 0,04987 | 20,79 | 193,1 | |||||
Вернуться к началу
Динамическая (абсолютная) и кинематическая вязкость воздуха при давлении 1 атмосфера, при температурах, указанных в ° C:
Для полного стола с кинематикой вязкость — поверните экран!
| Температура | Динамическая вязкость | Кинематическая вязкость | |||||||
| [° C] | [мкПа с], [Н с / м 2 * 10 -6 ] | [сП], [мПа с] | [фунт f с / фут 2 * 10-6] | [фунт м / фут / ч] | [сСт], [м 2 / с * 10 -6 ] | [футы 2 / с * 10 -4 ] | |||
| -75 | 13.18 | 0,01318 | 0,2753 | 0,03188 | 7,40 | 0,796 | |||
| -50 | 14,56 | 0,01456 | 0,3041 | 0,03523 | 9,22 | 0,992 | |||
| -25,89 | 0,01588 | 0,3317 | 0,03842 | 11,18 | 1,203 | ||||
| -15 | 16,40 | 0,01640 | 0.3425 | 0,03966 | 12,01 | 1,292 | |||
| -10 | 16,65 | 0,01665 | 0,3477 | 0,04028 | 12,43 | 1,338 | |||
| -5 | 16,90 | 0,0169030 | 0,04089 | 12,85 | 1,383 | ||||
| 0 | 17,15 | 0,01715 | 0,3582 | 0,04149 | 13.28 | 1,430 | |||
| 5 | 17,40 | 0,01740 | 0,3633 | 0,04209 | 13,72 | 1,477 | |||
| 10 | 17,64 | 0,01764 | 0,3685 | 0,04268 900 90 1,5 | |||||
| 15 | 17,89 | 0,01789 | 0,3735 | 0,04327 | 14,61 | 1,573 | |||
| 20 | 18.13 | 0,01813 | 0,3786 | 0,04385 | 15,06 | 1,621 | |||
| 25 | 18,37 | 0,01837 | 0,3836 | 0,04443 | 15,52 | 1.671 | |||
| 1,671 | |||||||||
| 0,3885 | 0,04500 | 15,98 | 1,720 | ||||||
| 40 | 19,07 | 0,01907 | 0.3983 | 0,04614 | 16,92 | 1,822 | |||
| 50 | 19,53 | 0,01953 | 0,4080 | 0,04725 | 17,88 | 1,925 | |||
| 60 | 19,99 | 0,0199935 0,0199990 0,0199990 | 18,86 | 2,030 | |||||
| 80 | 20,88 | 0,02088 | 0,4361 | 0,05051 | 20.88 | 2,248 | |||
| 100 | 21,74 | 0,02174 | 0,4541 | 0,05260 | 22,97 | 2,473 | |||
| 125 | 22,79 | 0,02279 | 0,4760 | 0,055138 | 0,02279 | 0,4760 | 0,0551387 | ||
| 150 | 23,80 | 0,02380 | 0,4971 | 0,05758 | 28,51 | 3,069 | |||
| 175 | 24.78 | 0,02478 | 0,5176 | 0,05995 | 31,44 | 3,384 | |||
| 200 | 25,73 | 0,02573 | 0,5374 | 0,06225 | 34,47 | 3,710 | |||
| 26,47 | 3,710 | ||||||||
| 26,47 | 0,5567 | 0,06448 | 37,60 | 4,047 | |||||
| 300 | 29,28 | 0,02928 | 0.6115 | 0,07083 | 47,54 | 5,117 | |||
| 412 | 32,87 | 0,03287 | 0,6865 | 0,07952 | 63,82 | 6,869 | |||
| 500 | 35,47 | 0,07 | 77,72 | 8,366 | |||||
| 600 | 38,25 | 0,03825 | 0,7988 | 0,09252 | 94.62 | 10,19 | |||
| 700 | 40,85 | 0,04085 | 0,8532 | 0,09883 | 112,6 | 12,12 | |||
| 800 | 43,32 | 0,04332 | 0,9047 | 0,1048 | 90 900|||||
| 900 | 45,66 | 0,04566 | 0,9535 | 0,1104 | 151,7 | 16,33 | |||
| 1000 | 47.88 | 0,04788 | 1.000 | 0,1158 | 172,7 | 18,59 | |||
| 1100 | 50,01 | 0,05001 | 1,045 | 0,1210 | 194,6 | 20,95 | 9 вверху 9 Преобразование единиц: Вязкость динамическая, абсолютная
См. Также Конвертер единиц абсолютной или динамической вязкости Кинематическая вязкость
| ||




 также
также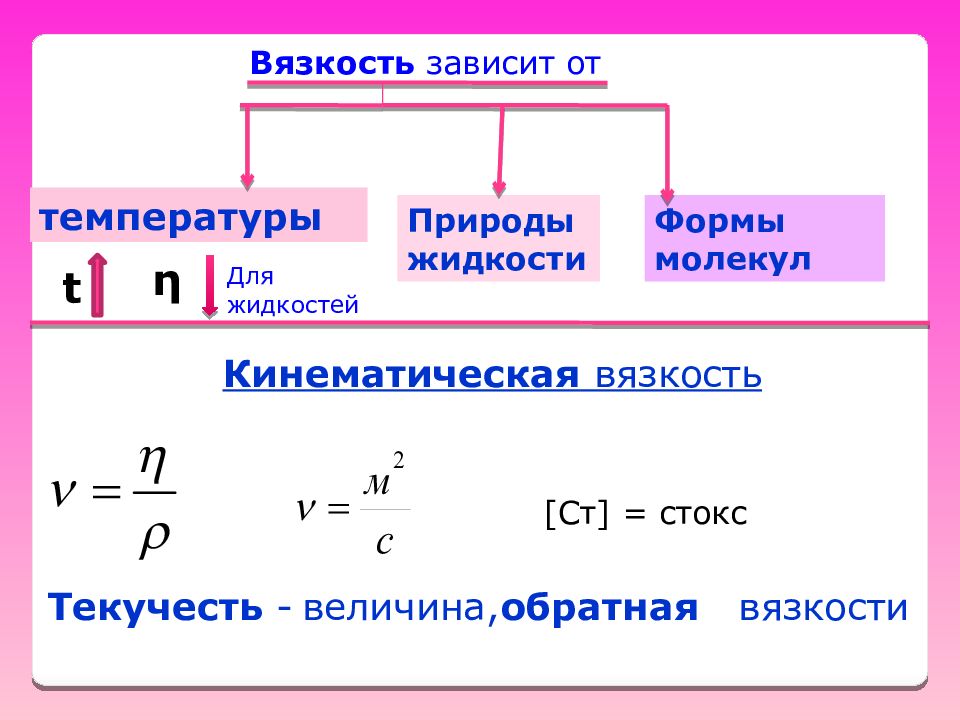 В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз).
В системе СИ динамическая вязкость выражается в Па×с (паскаль-секунда), внесистемная единица П (пуаз).

 2/2
2/2
 Уравнение
Ньютона.
Уравнение
Ньютона.